Метрология. Выборочный контроль

Случайное событие может произойти, а может нет. Вероятность, что оно произойдёт, измеряют числом р от 0 до 1 (от 0% до 100%).
Несколько событий бывают:
1. несовместными – может произойти только одно событие из группы; если оно произошло, то другие события уже не произойдут. Пример: автомобиль на перекрёстке может двигаться налево или направо.
1а несовместными, образующими полную группу – обязательно произойдёт одно из этих событий. Пример: автомобиль на перекрёстке может двигаться прямо, налево или направо.
1б противоположными – два события, образующие полную группу. Пример: студент либо пришёл на занятие, либо пропустил его.
2. совместными – одно событие не зависит от другого. Пример: событие 1 – сегодня четверг; событие 2 – сегодня идёт дождь.
Теория вероятностей

Вероятность одного события это отношение числа благоприятных исходов (при которых событие наступало) к общему числу опытов.
Пример: оценку «А» по метрологии в прошлые годы получили 5 студентов, а всего сдавали экзамен 40 студентов. Вероятность получить оценку «А» 5/40=12,5%
Вероятности несовместных событий суммируются. Сумма вероятностей несовместных событий, образующих полную группу, равна 100%.
Пример 1: вероятность того, что студент получит на экзамене оценку «А» – 25%, оценку «В» – 20%. Вероятность того, что студент получит оценку выше «С» 20%+25%=45%.
Пример 2: вероятность того, что упомянутый выше студент получит «С» – 20%, «D» - 15%, «Е» – 10%. Вероятность того, что студент не сдаст экзамен 100%-25%-2*20%-15%-10%=10%.
Вероятность одновременного наступления совместных событий равна произведению их вероятностей.
Пример: преподаватель пообещал поставить студенту Иванову зачёт «автоматом» после дождичка в четверг. Вероятность того, что по расписанию зачёт будет в четверг 1/7=15%; вероятность дождя в июне 20%. Вероятность, что студент получит зачёт «автоматом» 15%*20%=3%
Теория вероятностей

Пусть в ящике много шаров двух цветов: 80% белых шаров и 20% черных. Из ящика случайным образом извлекают 3 шара. Какие возможны исходы данного опыта, с какой вероятностью они наступят?
Исход 1: 3 белых шара. Вероятность 80%*80%*80%=51,2%
Исход 2: 2 белых шара и 1 чёрный. Тут сложнее:
Б+Б+Ч, вероятность 80%*80%*20%=12,8%
Б+Ч+Б, вероятность 80%*20%*80%=12,8%
Ч+Б+Б, вероятность 20%*80%*80%=12,8%
Итого вероятность исхода 2: 12,8%+12,8%+12,8%=38,4%.
Исход 4: 3 черных шара. Вероятность 20%*20%*20%=0,8%
Исход 3: 1 белый шар и 2 чёрных. Вероятность 100%-51,2%-38,4%-0,8%=9,6%
Теория вероятностей

Формула Бернулли

Модернизируем нашу задачу. Изготовитель поставляет потребителю партию деталей. Согласно контракту, 80% должны быть годными. Процедура приёмки определена в контракте следующим образом: проверяют 3 детали, потребитель принимает партию, если из проверенных не более одной детали окажется бракованными, и возвращает партию поставщику, если среди проверенных окажется две или более бракованных деталей.
Приемлемый уровень качества AQL = 20% - доля бракованных деталей, которая устраивает потребителя.
Приёмочное число Ас = 1 – число бракованных изделий среди проверенных, при котором партию принимают.
Браковочное число Re = 2 – число бракованных изделий среди проверенных, при котором партию бракуют.
Объем выборки n = 3 – число деталей, которые подвергают контролю.
Как видим, вероятность принять партию = вероятность Исход1 + Исход2: 51,2%+38,4% = 89,6%
Вероятность отвергнуть партию = вероятность Исход4 + Исход3: 9,6%+0,8% = 10,4%
Выборочный контроль

Риск изготовителя: вероятность того, что партию деталей отвергнут по результатам контроля, хотя она полностью соответствует условиям контракта. В нашем случае, риск изготовителя = 10,4%.
Риск потребителя: вероятность принять партию деталей, качество которой хуже заявленного. Например, если долю годных деталей понизить до 79%, то вероятность принять партию составит 88,6%; если понизить до 60% - 64,8%, понизить до 40% - 35,2%...
Выборочный контроль

.
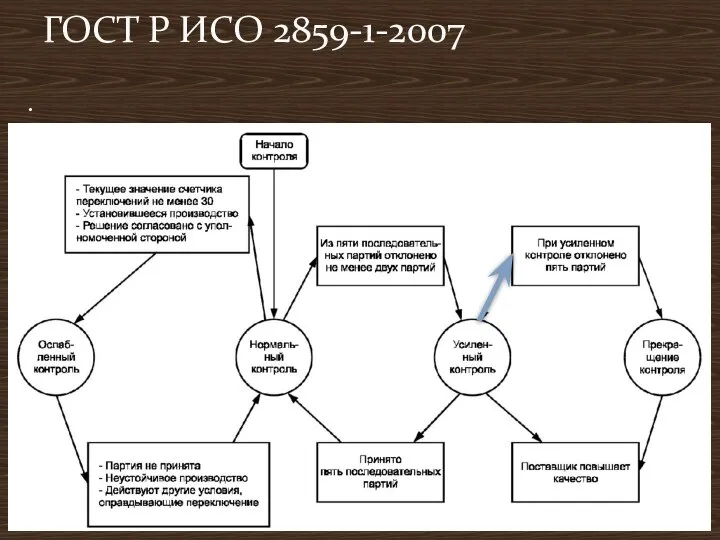
ГОСТ Р ИСО 2859-1-2007

Одно- двух- многоступенчатый контроль: при больших партиях и малом AQL приходится контролировать выборки большого объёма. Стандарт предусматривает возможность принять решение об отбраковке партии до того, как проконтролирована вся выборка.
Планы нормального, усиленного и ослабленного контроля – стандарт предусматривает сокращение объёма контроля в случае предыдущих качественных поставок и наоборот, ужесточение контроля при нарушении требований к качеству.
ГОСТ Р ИСО 2859-1-2007

.
ГОСТ Р ИСО 2859-1-2007

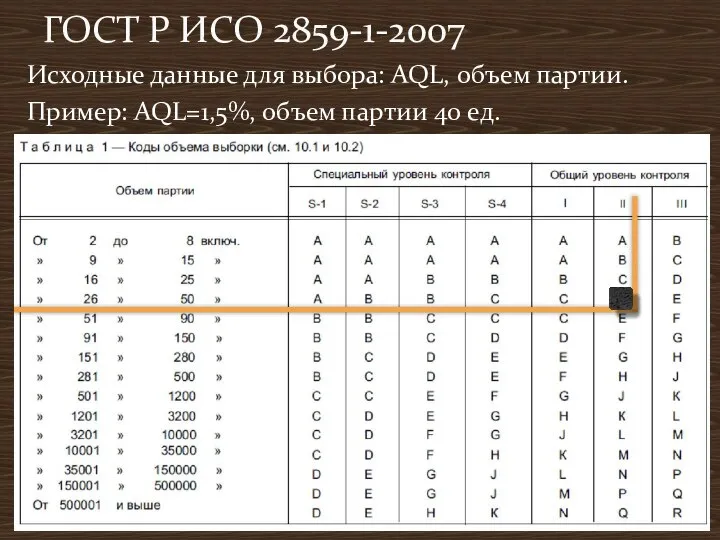
Исходные данные для выбора: AQL, объем партии.
Пример: AQL=1,5%, объем партии 40 ед.
ГОСТ Р ИСО 2859-1-2007

При одноступенчатом нормальном контроле нужно контролировать 8 деталей из партии. Если дефектных деталей не будет, партию принимают, если хотя бы одна деталь окажется дефектной – партию бракуют.
ГОСТ Р ИСО 2859-1-2007

При одноступенчатом усиленном контроле нужно контролировать 13 деталей из партии. Если дефектных деталей не будет, партию принимают, если хотя бы одна деталь окажется дефектной – партию бракуют.
ГОСТ Р ИСО 2859-1-2007

При одноступенчатом ослабленном контроле нужно контролировать только 3 детали из партии. Если дефектных деталей не будет, партию принимают, если хотя бы одна деталь окажется дефектной – партию бракуют.
ГОСТ Р ИСО 2859-1-2007

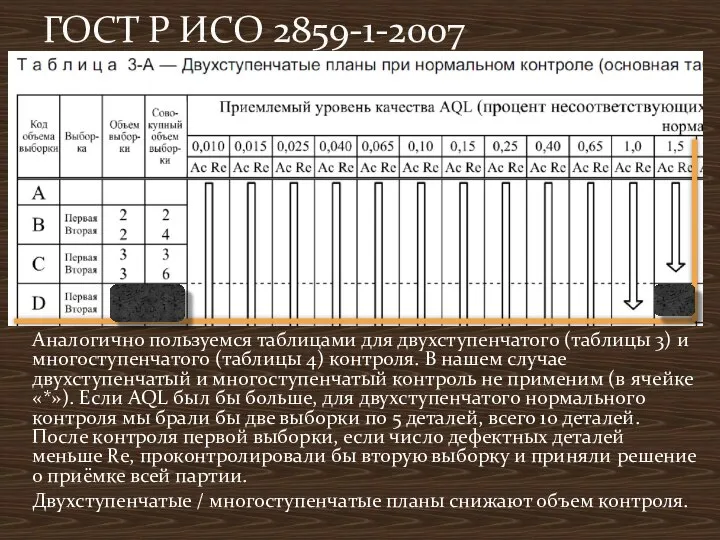
Аналогично пользуемся таблицами для двухступенчатого (таблицы 3) и многоступенчатого (таблицы 4) контроля. В нашем случае двухступенчатый и многоступенчатый контроль не применим (в ячейке «*»). Если AQL был бы больше, для двухступенчатого нормального контроля мы брали бы две выборки по 5 деталей, всего 10 деталей. После контроля первой выборки, если число дефектных деталей меньше Re, проконтролировали бы вторую выборку и приняли решение о приёмке всей партии.
Двухступенчатые / многоступенчатые планы снижают объем контроля.
ГОСТ Р ИСО 2859-1-2007

Вернёмся к теории вероятности.
Риск изготовителя. Вероятность того, что отдельная деталь бракованная, составляет 1,5%. Вероятность выбрать 8 годных деталей (1-AQL)8 =(98,5%)8=88,6%, т.е. риск изготовителя 11,4%. Это число приведено в таблице 5-А. Вообще, планы контроля подобраны в стандарте так, чтобы при общем уровне контроля II риск изготовителя был чуть больше 10%. При усиленном контроле риск изготовителя больше, при ослабленном – меньше.
Риск потребителя. До какой степени можно увеличивать AQL, чтобы вероятность забраковать партию выросла до 90%? (1-AQL)8=10%, откуда (1-AQL)=75% или AQL=25%. Это число называется «качество риска потребителя» и приведено в таблице 6.
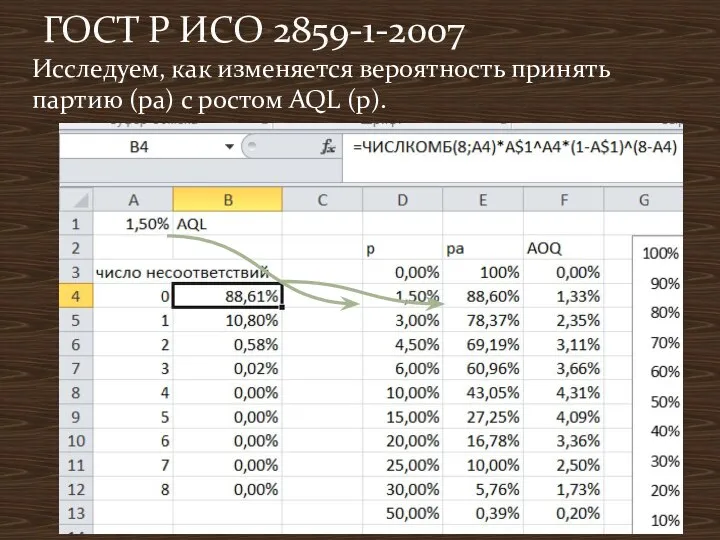
ГОСТ Р ИСО 2859-1-2007

Исследуем, как изменяется вероятность принять партию (pa) с ростом AQL (p).
ГОСТ Р ИСО 2859-1-2007

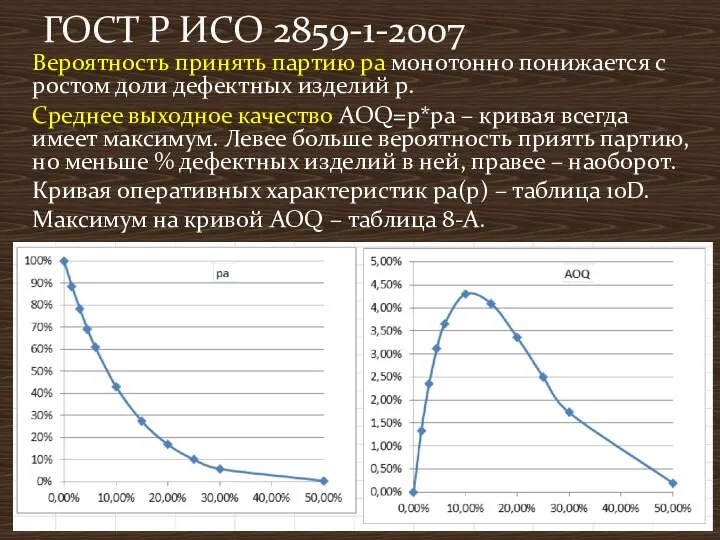
Вероятность принять партию ра монотонно понижается с ростом доли дефектных изделий p.
Среднее выходное качество AOQ=p*pa – кривая всегда имеет максимум. Левее больше вероятность приять партию, но меньше % дефектных изделий в ней, правее – наоборот.
Кривая оперативных характеристик ра(р) – таблица 10D.
Максимум на кривой AOQ – таблица 8-А.
ГОСТ Р ИСО 2859-1-2007

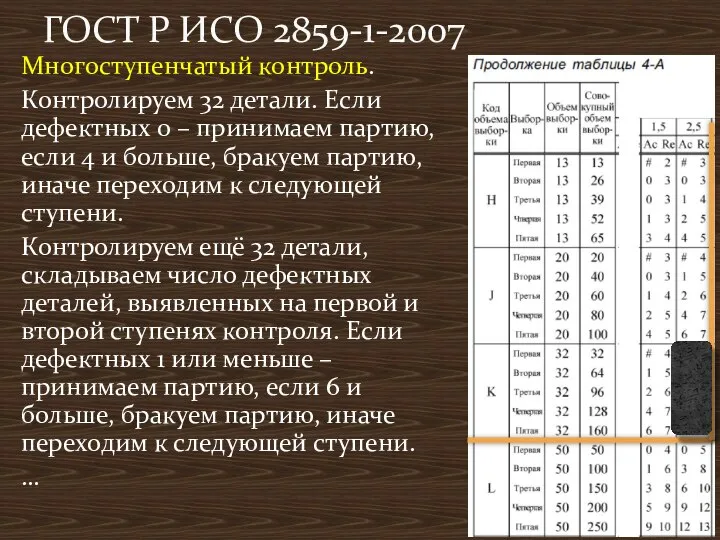
Многоступенчатый контроль.
Контролируем 32 детали. Если дефектных 0 – принимаем партию, если 4 и больше, бракуем партию, иначе переходим к следующей ступени.
Контролируем ещё 32 детали, складываем число дефектных деталей, выявленных на первой и второй ступенях контроля. Если дефектных 1 или меньше – принимаем партию, если 6 и больше, бракуем партию, иначе переходим к следующей ступени.
…
ГОСТ Р ИСО 2859-1-2007