Содержание
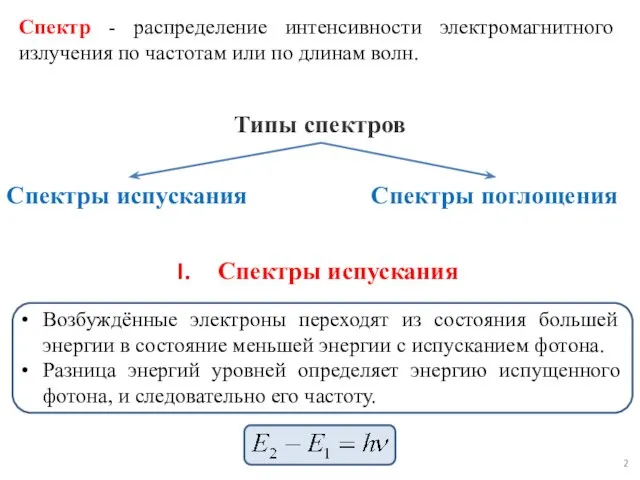
- 2. Спектр - распределение интенсивности электромагнитного излучения по частотам или по длинам волн. Типы спектров Спектры испускания
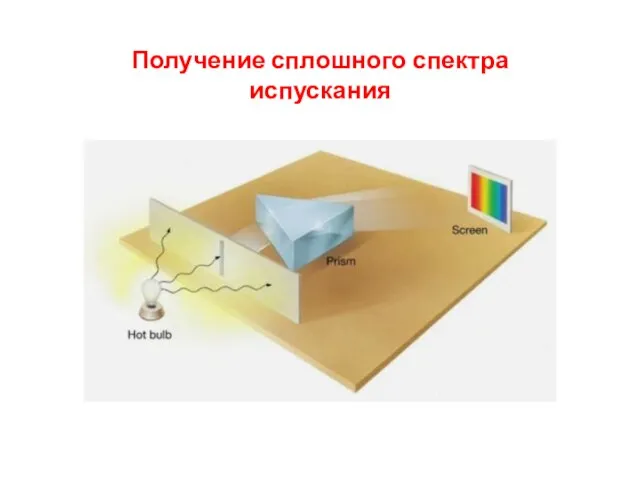
- 3. Получение сплошного спектра испускания
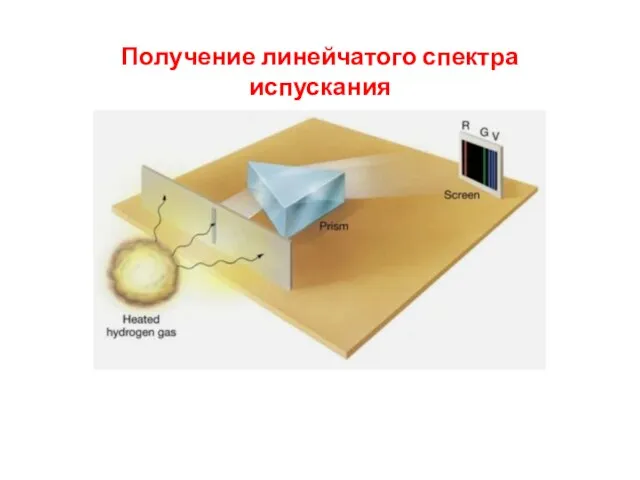
- 4. Получение линейчатого спектра испускания
- 5. Сплошной - это спектр, содержащий все длины волны определенного диапазона от красного и до фиолетового. Сплошной
- 6. Спектры поглощения Спектры поглощения получают, пропуская свет от источника, дающего сплошной спектр, через вещество, атомы которого
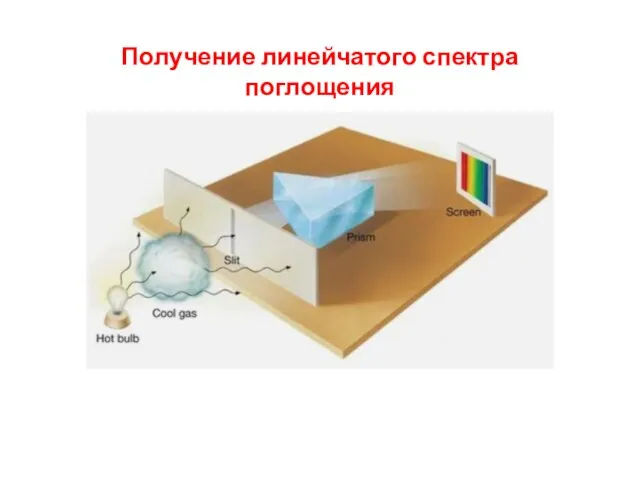
- 7. Получение линейчатого спектра поглощения
- 8. Метод определения качественного и количественного состава вещества по его спектру называется спектральным анализом. Количественное содержание элемента
- 9. В 1868 г. французский астроном Жансен наблюдал в Индии полное солнечное затмение и спектроскопически исследовал хромосферу
- 10. Гелий занимает второе место по распространённости во Вселенной после водорода — около 23 % по массе.
- 11. Было замечено, что линии в спектрах атомов расположены не беспорядочно, а объединяются в группы - серии
- 12. R' =1,10·107 м-1 – постоянная Ридберга. R=R’ ·c = 3,29·1015 с-1 – постоянная Ридберга. Бальмер Иоганн
- 13. С увеличением n линии серии сближаются; значение n=∞ определяет границу серии, к которой со стороны бо́льших
- 14. В инфракрасной области спектра: серия Пашена серия Брэкета серия Пфунда
- 16. Все вышеперечисленные серии в спектре атома водорода могут быть описаны формулой – обобщённой формулой Бальмера: m=1,2,3,4,5,6
- 17. Ядерная (планетарная) модель атома 1911 год. Эрнест Резерфорд. Суть опыта: источник создаёт узкий пучок α-частиц, который
- 18. 1. Подавляющее число α-частиц проходит через образец-фольгу, почти не испытывая отклонения. Была обнаружена неоднородность вещества. В
- 19. 1. В центре атома расположено ядро, в котором сосредоточена почти вся масса атома и весь положительный
- 20. 1. Оценка размера ядра атома (его радиус ≈ 10-15 м). Достижения модели Резерфорда 2. Оценка заряда
- 21. 1. Если электрон вращается вокруг ядра, то он обладает нормальным ускорением (т.е. движется ускоренно). В этом
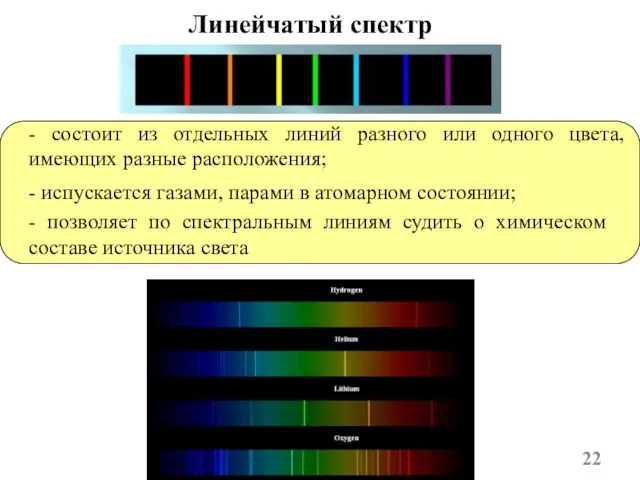
- 22. Линейчатый спектр - состоит из отдельных линий разного или одного цвета, имеющих разные расположения; - испускается
- 23. На самом деле электроны не вращаются по орбитам как планеты солнечной системы вокруг Солнца. Важно!!! Электрон
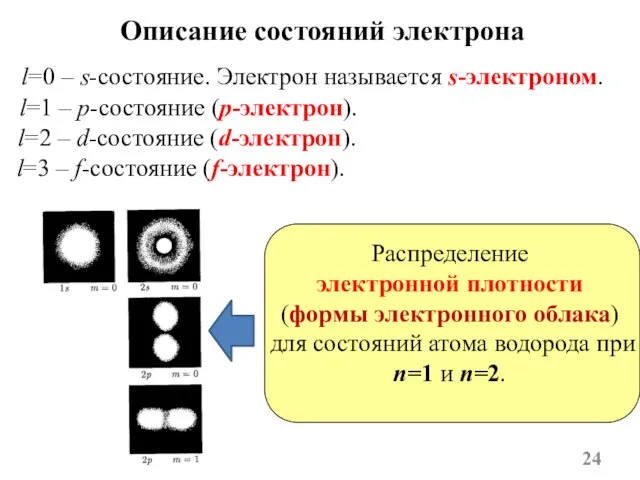
- 24. l=0 – s-состояние. Электрон называется s-электроном. Описание состояний электрона l=1 – p-состояние (p-электрон). l=2 – d-состояние
- 25. Постулаты Бора 1913 год. Нильс Бор предпринял попытку построить модель атома на основе квантовых представлений. Его
- 26. 1. Электрон в атоме может находиться в стационарных состояниях, в которых электрон движется по круговым орбитам
- 27. 2. Находясь в стационарном состоянии электрон не излучает и не поглощает энергию. 3. При переходе электрона
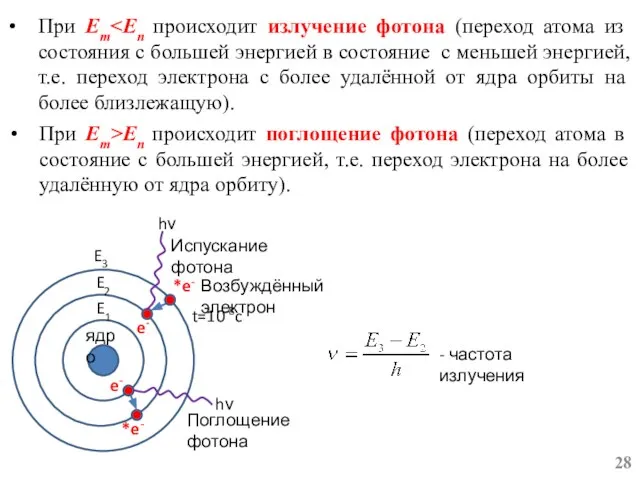
- 28. При Em При Em>En происходит поглощение фотона (переход атома в состояние с большей энергией, т.е. переход
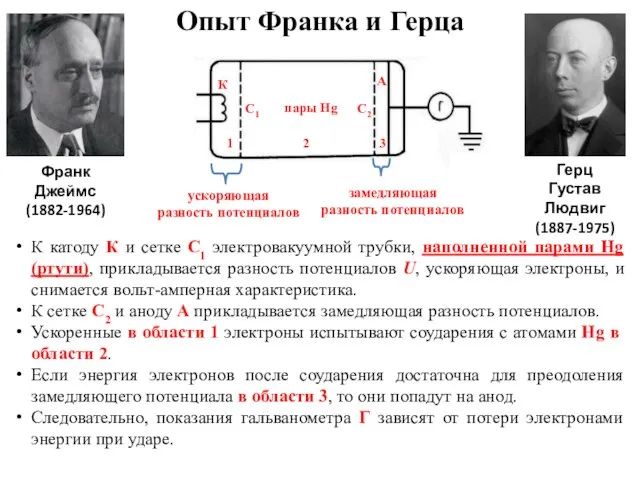
- 29. Опыт Франка и Герца Франк Джеймс (1882-1964) Герц Густав Людвиг (1887-1975) К катоду К и сетке
- 30. Сила тока вначале монотонно возрастала, достигая максимума при U = 4,9В, после чего с дальнейшим увеличением
- 31. Когда энергия, накапливаемая электроном в промежутке катод-сетка, достигает значения ΔЕ1 соударения становятся неупругими — электроны при
- 32. Опыт Франка и Герца показал, что спектр поглощаемой атомом энергии не непрерывен, а дискретен! (минимальная порция
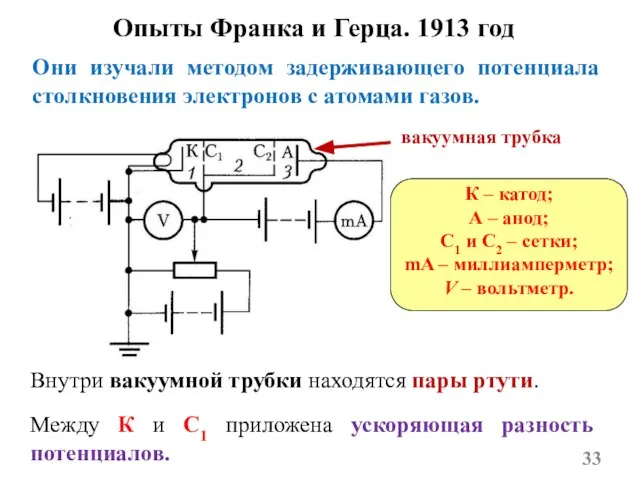
- 33. Опыты Франка и Герца. 1913 год Они изучали методом задерживающего потенциала столкновения электронов с атомами газов.
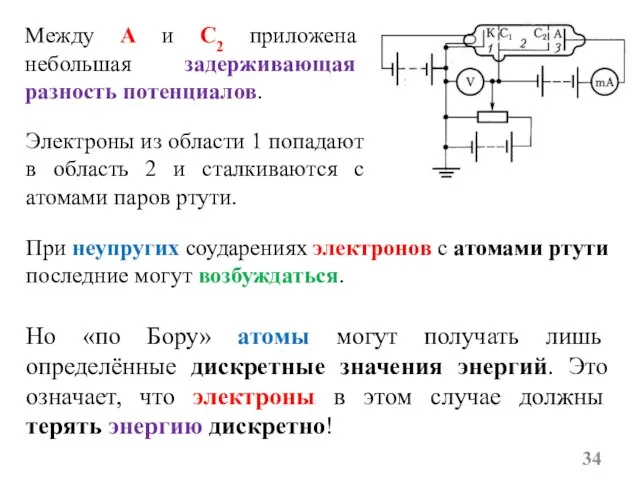
- 34. Электроны из области 1 попадают в область 2 и сталкиваются с атомами паров ртути. Между А
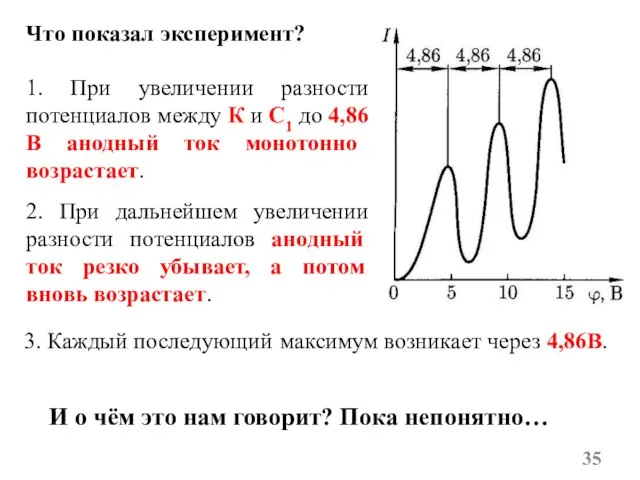
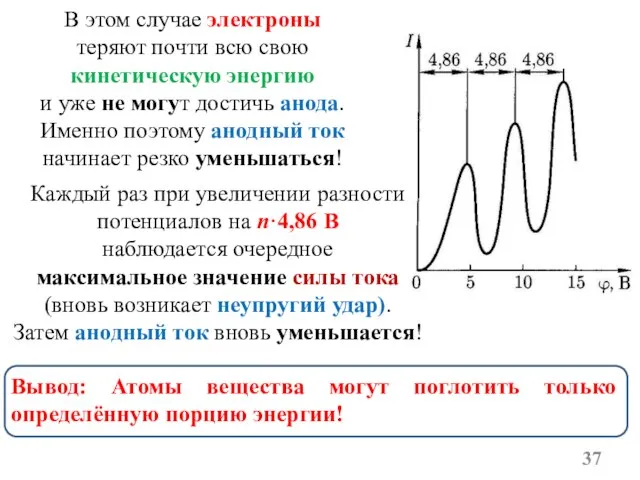
- 35. Что показал эксперимент? 1. При увеличении разности потенциалов между К и C1 до 4,86В анодный ток
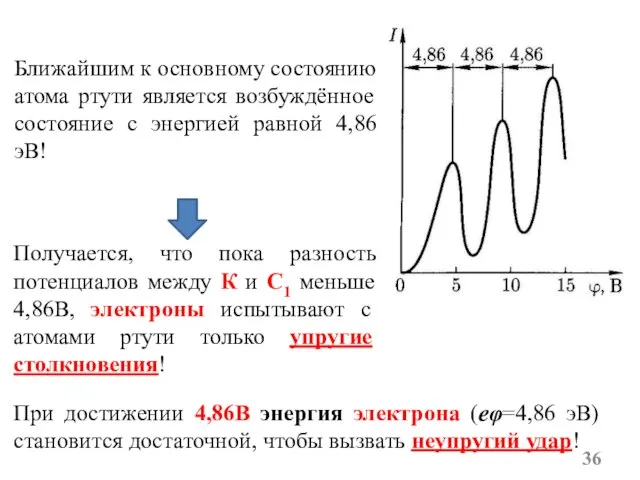
- 36. Ближайшим к основному состоянию атома ртути является возбуждённое состояние с энергией равной 4,86эВ! Получается, что пока
- 37. Каждый раз при увеличении разности потенциалов на n·4,86 В наблюдается очередное максимальное значение силы тока (вновь
- 38. Опыт Франка и Герца показал, что спектр поглощаемой атомом энергии не непрерывен, а дискретен! (минимальная порция
- 39. Рассмотрим вращение электрона по круговой стационарной орбите. Момент импульса электрона должен удовлетворять условию Электрон движется с
- 40. Получим: выражение для радиусов допустимых орбит: выражение для дозволенных дискретных значений энергий электрона в атоме
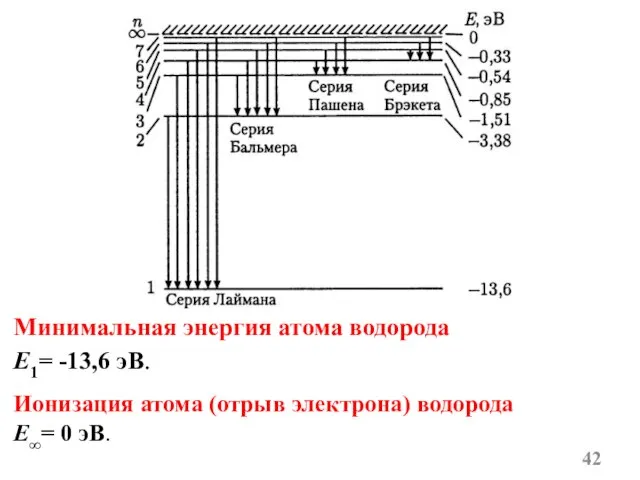
- 41. Главное квантовое число n (целое число) определяет энергетические уровни атома. Основное состояние – энергетическое состояние с
- 42. Минимальная энергия атома водорода E1= -13,6 эВ. Ионизация атома (отрыв электрона) водорода E∞= 0 эВ.
- 43. При переходе атома водорода (Z=1) из стационарного состояния n в стационарное состояние m с меньшей энергией
- 44. Достижения теории Бора Теория Бора практически точно описала все частоты излучения атома водорода, и стал ясен
- 45. Кроме водородоподобного атома, эта теория больше ничего объяснить не сумела. Неудачи теории Бора Вопрос «Почему»? Теория
- 46. Гипотеза де Бройля 1923 год. Луи де Бройль выдвинул гипотезу об универсальности корпускулярного-волнового дуализма. С каждым
- 47. Любой микрочастице сопоставляется волновой процесс, длина волны которого определяется по формуле де Бройля: Эта гипотеза была
- 48. А как быть с макроскопическими телами? Для частицы массой 5г, движущейся со скоростью 1м/с, соответствует волна
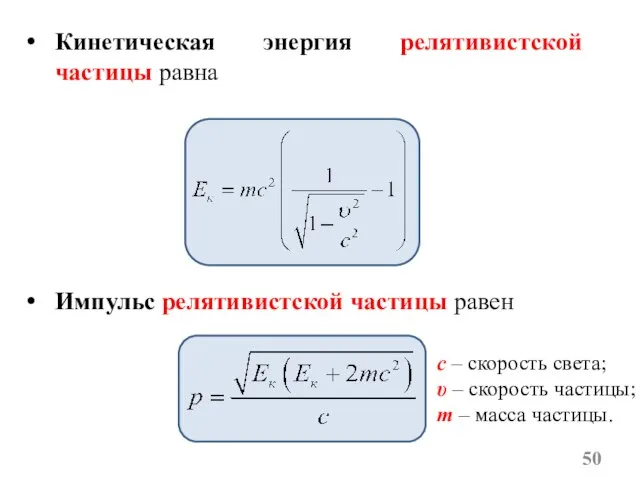
- 49. Любая частица может в разных ситуациях являться либо классической частицей, либо релятивистской. Как определить какая частица
- 50. Импульс релятивистской частицы равен c – скорость света; υ – скорость частицы; m – масса частицы.
- 51. Эти волны не являются физическими материальными волнами, их принято трактовать как волны вероятности. Физический смысл имеет
- 52. Свойства микрочастиц Отличие микрочастицы от макрочастицы заключается в том, что она не обладает одновременно определенными значениями
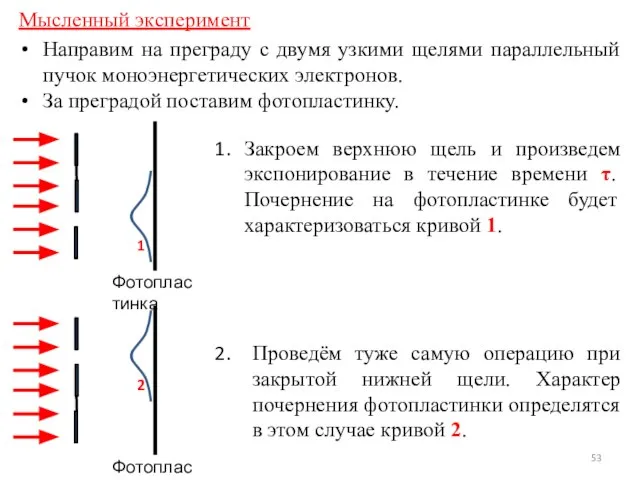
- 53. Направим на преграду с двумя узкими щелями параллельный пучок моноэнергетических электронов. За преградой поставим фотопластинку. Мысленный
- 54. Характер картины свидетельствует о том, что на движение каждого электрона оказывают влияние оба отверстия!!! Такой вывод
- 55. Нельзя приписывать микрочастицам одновременно корпускулярные свойства и волновые! 1927 год. Неопределённость Гейзенберга В классической механике у
- 56. Это означает, что микрочастица с определённым импульсом имеет полностью неопределённую координату и наоборот! Соотношение неопределённостей Гейзенберга:
- 57. Если микрочастица находится в состоянии с точным значением координаты (Δx=0), то в этом состоянии соответствующая проекция
- 58. Перепишем соотношение неопределённостей к следующему виду Чем больше масса частицы, тем меньше неопределённость её координаты и
- 59. Пример 1. Пусть пучок электронов движется вдоль оси x со скоростью v=108м/с, определяемой с точностью до
- 60. Пример 2. Пусть электрон движется в поле ядра атома. Допустим, что неопределённость координаты электрона прядка линейного
- 61. Соотношение неопределённости Гейзенберга для энергии ΔE – неопределённость энергии некоторого квантового состояния системы; Δt – (неопределённость
- 63. Скачать презентацию











































 Швейная машина. История и устройсво
Швейная машина. История и устройсво Инструменты, механизмы и технические устройства
Инструменты, механизмы и технические устройства Аномальність фізичних властивостей води
Аномальність фізичних властивостей води Законы постоянного тока
Законы постоянного тока Презентация на тему Строение вещества
Презентация на тему Строение вещества  Формульный диктант Кинематика, законы Ньютона, сохранения, статика
Формульный диктант Кинематика, законы Ньютона, сохранения, статика Механика. Повторение. Занятие 7
Механика. Повторение. Занятие 7 Машиноведение
Машиноведение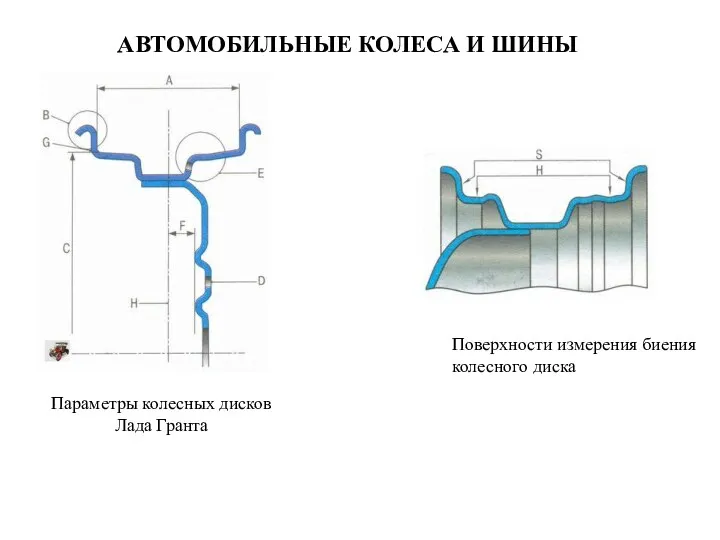 Автомобильные колеса и шины. Поверхности измерения биения колесного диска. Параметры колесных дисков Лада Гранта
Автомобильные колеса и шины. Поверхности измерения биения колесного диска. Параметры колесных дисков Лада Гранта Инновационная концепция электронного корабля
Инновационная концепция электронного корабля Решение задач по теме Тепловые явления. Агрегатные состояния вещества
Решение задач по теме Тепловые явления. Агрегатные состояния вещества Электрическое поле. Лекция № 1
Электрическое поле. Лекция № 1 Волокна большого диаметра. Анализ фазового состава, макро- и микроструктуры полуфабрикатов и готовых изделий из B-Al
Волокна большого диаметра. Анализ фазового состава, макро- и микроструктуры полуфабрикатов и готовых изделий из B-Al Теория деформаций. Практическое занятие
Теория деформаций. Практическое занятие Сцепление. Тесты к теоретическим занятиям
Сцепление. Тесты к теоретическим занятиям Сила трения. Опыт №1. Наблюдение явления трения
Сила трения. Опыт №1. Наблюдение явления трения Презентация на тему КПД тепловых двигателей (8 класс)
Презентация на тему КПД тепловых двигателей (8 класс)  Акустичне явище грім
Акустичне явище грім Механика и элементы специальной теории относительности
Механика и элементы специальной теории относительности Бионика. Аэродинамические прототипы
Бионика. Аэродинамические прототипы давл жидк
давл жидк Электризация. Взаимодействие заряженных тел
Электризация. Взаимодействие заряженных тел Цепь переменного тока с индуктивностью
Цепь переменного тока с индуктивностью Машины и механизмы
Машины и механизмы Общие принципы инженерных расчетов
Общие принципы инженерных расчетов Škoda Octavia. Кузов. Оборудование кузова
Škoda Octavia. Кузов. Оборудование кузова Драйвер двигателя постоянного тока. Вспомогательные функции
Драйвер двигателя постоянного тока. Вспомогательные функции Викторина по физике
Викторина по физике