Вихрь (ротор) векторного поля

Теорема Умова – Пойтинга. Вектор Пойтинга. Теорема подобия. Граничные задачи электродинамики.

Для определения энергии во всём объёме проинтегрируем выражение по объёму V .

характеризует значение и направление перемещения энергии, проходящей в единицу времени через единицу площади, перпендикулярной вектору Пойнтинга

Теорема Умова - Пойнтинга в комплексной форме
поток комплексного вектора Пойнтинга сквозь замкнутую поверхность равен комплексной мощности, выделяемой внутри объёма, ограниченного этой поверхностью.

Сила постоянного тока I .
Напряжение между жилой и оболочкой U . Проводимость материала жилы и оболочки γ .
Мощность сигнала, передаваемого по кабелю,
P = IU .
Рассчитать поток вектора Пойнтинга через поперечное сечение диэлектрика,
заполняющего пространство между жилой и оболочкой.

Нормальная составляющая вектора напряжённости электрического поля Еn в диэлектрике через напряжение U для коаксиального контура определяется
где R1 – радиус жилы; R2 – внутренний радиус оболочки.
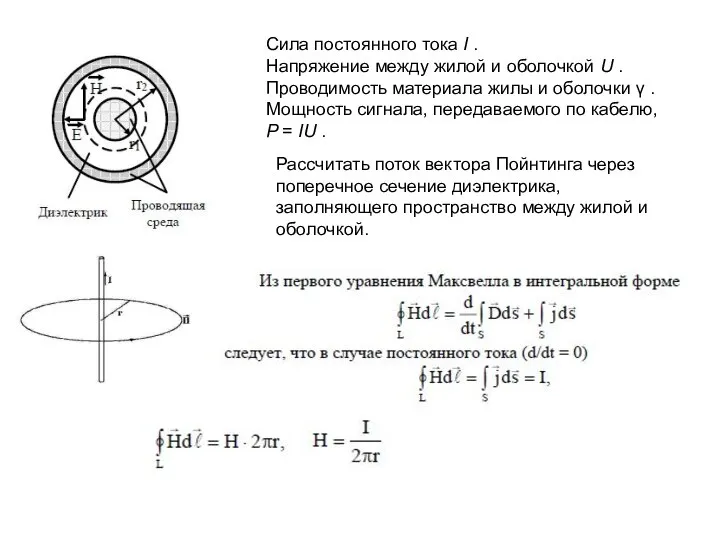
Тогда тангенциальная составляющая вектора Пойнтинга для точек диэлектрика на расстоянии r от оси ( R 1 ≤ r ≤ R 2 ) определяется выражением
Поток вектора Пойнтинга через кольцо диэлектрика с радиусами R1 и R2 :
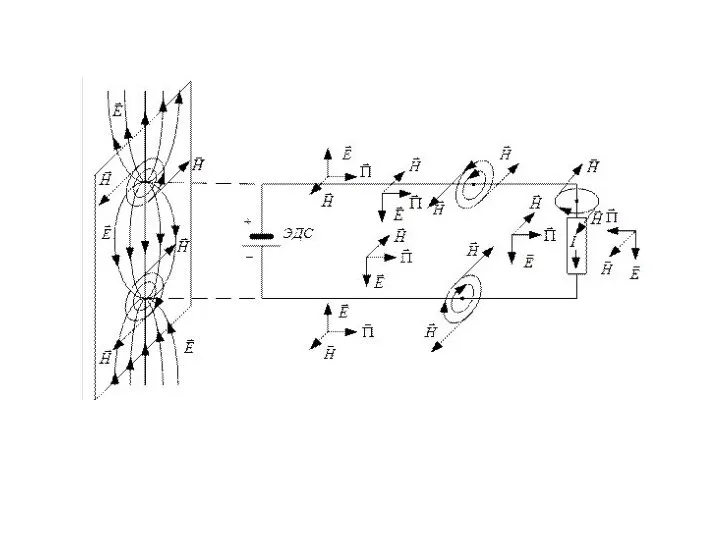
Электромагнитная энергия от места её генерирования к месту потребления передаётся по диэлектрику; провода являются каналами, по которым проходит ток, и организаторами структуры поля в диэлектрике. По жиле и оболочке энергия к приёмнику не передаётся. Провода сами потребляют из диэлектрика энергию на покрытие тепловых потерь.

СРСП РЕФЕРАТ: «Поток вектора Пойнтинга в плоскопараллельном конденсаторе»
Приложить расчет, показать направление потока. (3-4 страницы)

Напряженность электрического поля равномерно заряженной тонкой проволоки бесконечной длины. Найдем зависимость напряженности электрического поля равномерно заряженной тонкой проволоки бесконечной длины от расстояния r до оси проволоки, используя теорему Гаусса. Выделим участок проволоки конечной длины L . Если линейная плотность заряда на проволоке λ, то заряд выделенного участка равен q = λ L .

http://www.math24.ru/