Гидродинамика

Таким образом, по показанию пьезометра определяем статический напор:

Для определения полного напора по оси потока пользуются трубкой Пито. Это трубка очень малого диаметра с загнутым под углом 900 и гладко обработанным концом. Трубка Пито устанавливается по оси трубы или в любой другой точке потока так, чтобы скорость и была направлена на входное отверстие трубки.

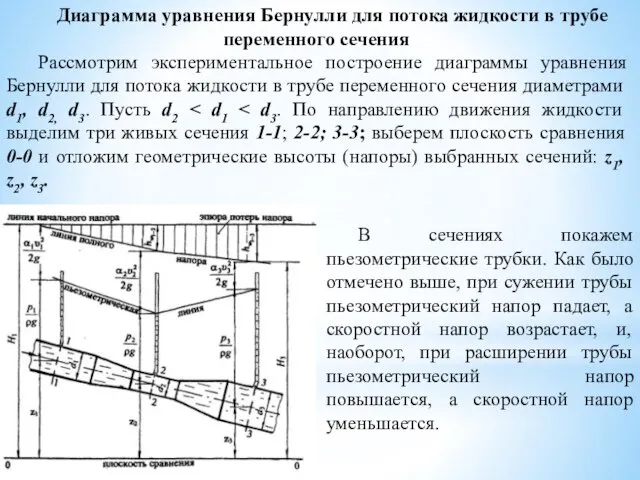
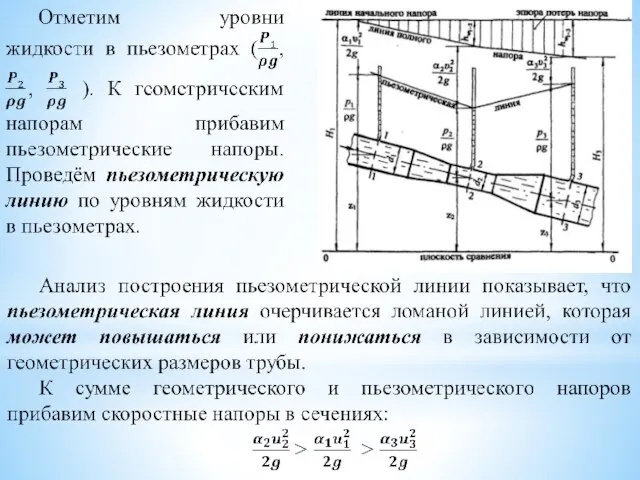
Диаграмма уравнения Бернулли для потока жидкости в трубе переменного сечения
Рассмотрим экспериментальное построение диаграммы уравнения Бернулли для потока жидкости в трубе переменного сечения диаметрами d1, d2, d3. Пусть d2 < d1 < d3. По направлению движения жидкости выделим три живых сечения 1-1; 2-2; 3-3; выберем плоскость сравнения 0-0 и отложим геометрические высоты (напоры) выбранных сечений: z1, z2, z3.
В сечениях покажем пьезометрические трубки. Как было отмечено выше, при сужении трубы пьезометрический напор падает, а скоростной напор возрастает, и, наоборот, при расширении трубы пьезометрический напор повышается, а скоростной напор уменьшается.

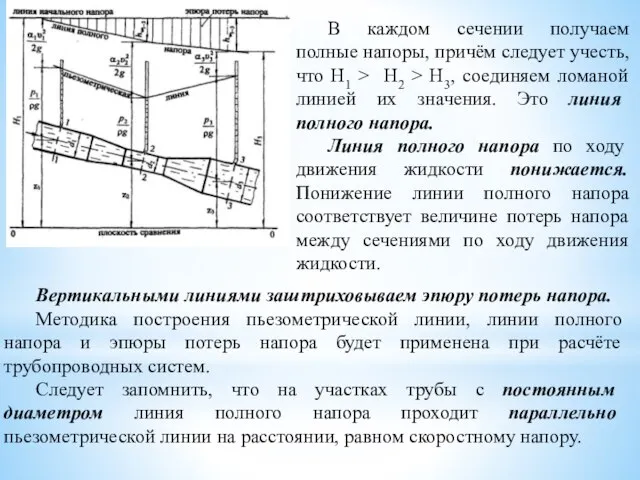
Вертикальными линиями заштриховываем эпюру потерь напора.
Методика построения пьезометрической линии, линии полного напора и эпюры потерь напора будет применена при расчёте трубопроводных систем.
Следует запомнить, что на участках трубы с постоянным диаметром линия полного напора проходит параллельно пьезометрической линии на расстоянии, равном скоростному напору.
В каждом сечении получаем полные напоры, причём следует учесть, что H1 > H2 > H3, соединяем ломаной линией их значения. Это линия полного напора.
Линия полного напора по ходу движения жидкости понижается. Понижение линии полного напора соответствует величине потерь напора между сечениями по ходу движения жидкости.

Методика составления уравнения Бернулли для решения теоретических и инженерных задач
С помощью уравнения Бернулли решаются многие теоретические и практические задачи. Применение уравнения Бернулли предусмотрено для реальной, вязкой жидкости при установившемся движении для тех сечений, где движение не должно быть резко изменяющимся.
На использовании уравнения Бернулли основано создание приборов для измерения скорости и расхода потока жидкости.
При составлении уравнения Бернулли следует пользоваться следующей методикой.
1. Выбираются два сечения, в которых известно наибольшее количество параметров, входящих в уравнение, или их нужно определить. Такими сечениями служат свободная поверхность жидкости или места установки измерительных приборов (манометров, вакуумметров, пьезометров и им подобных). Сечения проводятся горизонтально по свободной поверхности (для практических расчётов скорость на свободной поверхности принимается равной нулю, u = 0) или нормально к направлению движения жидкости, т. е. по живому сечению.

2 Сечения нумеруются по направлению движения жидкости. Это обусловлено тем, что потери напора в гидравлических сопротивлениях увеличиваются по направлению движения жидкости, и дополнительный член уравнения hw, учитывающий эти потери, должен быть со знаком плюс.
3 В уравнении Бернулли рекомендуется учитывать абсолютное давление в выбранных сечениях. Это позволит избежать ошибок при определении давления в сечениях.
4 Выбирается плоскость сравнения 0-0. Как правило, она совмещается с одним из сечений или проводится через его ось, тогда геометрическая высота этого сечения равна нулю (z = 0). Следует помнить, что плоскость сравнения всегда горизонтальная. Отсчёты геометрической высоты сечения z от плоскости сравнения вверх считаются положительными, вниз - отрицательными.
5 Уравнение Бернулли записывается в общем виде. Под уравнением представляются значения параметров. Производится подстановка всех величин в уравнение в буквенном выражении. Уравнение решается относительно неизвестного параметра.

Приборы для измерения скорости и расхода, основанные на уравнении Бернулли
Расходомер Вентури - это труба с плавным переходом от большего диаметра к меньшему, небольшой цилиндрической вставки меньшего диаметра и плавного перехода от меньшего диаметра к большему. В широкой и узкой части расходомера подключены приборы для измерения давления, например пьезометры, по показаниям которых рассчитывается скорость и расход неразрывного потока. Как правило, соотношение диаметров принимается равным: d2:d1 = 1/2; 1/3 и тому подобным.
Для определения скорости и расхода жидкости воспользуемся уравнением Бернулли. Пусть представленный прибор является водомером.

5 Запишем уравнение Бернулли в общем виде:

Из рисунка следует
значит

Анализируя формулу, видим, что расход жидкости является функцией разности показаний пьезометров (h) или показания другого прибора для измерения разности напоров.
Расходомер Вентури используется не только для капельных жидкостей, но и для газообразных. В этом случае в широкой и узкой частях расходомера выводятся штуцера, к которым подсоединяется жидкостный прибор для измерения разности давлений, например U-образный манометр или микроманометр с наклонной трубкой.
Входной коллектор. Входной коллектор используется для определения скорости и расхода во всасывающих воздушных, газовых, вентиляционных, пневмотранспортных и других системах.
Входной коллектор устанавливается на входе в систему и представляет трубу с плавным входом, выполненным по какому-либо криволинейному закону, например по параболе, так, чтобы исключить потери напора на входе в коллектор.

На расстоянии 3-5 диаметров трубы от входа выводится штуцер, к которому подключается жидкостный прибор для измерения давления (U­образный манометр, микроманометр). Рабочей жидкостью в приборе может быть вода, спирт или другая капельная жидкость. По показанию прибора (h) рассчитывается средняя скорость потока газообразной жидкости в трубе и её расход.
Покажем расчёт скорости и расхода газообразной жидкости во всасывающей системе, пользуясь уравнением Бернулли.
1 Выберем два сечения по кромке входного сечения коллектора, где скорость ещё практически отсутствует, и в месте установки измерительного прибора. Сечения проведём нормально к направлению движения жидкости, например воздуха.

Покажем расчёт скорости и расхода газообразной жидкости во всасывающей системе, пользуясь уравнением Бернулли.
2 Пронумеруем сечения 1-1 и 2-2 по напрaвлению движения воздуха.
3 Учтём абсолютное давление в выбранных сечениях. Абсолютное давление в первом сечении р1 = ра. Абсолютное давление во втором сечении будет меньше атмосферного, так как всасывание идёт за счёт создания вакуума. Пользуясь уравнениями гидростатики, составим условие равенства давления относительно плоскости уровня О-О в U-образном манометре, получим абсолютное давление во втором сечении
р2=ра –ρжидкgh.

Подставим скорость v1 в уравнение для h:
Расход без учета потерь напора (теоретический расход)

Подставляя числовые значения

Потери напора по длине при турбулентном режиме
Турбулентное течение жидкости является наиболее распространённым в технике, но представляет в то же время одно из сложных гидравлических процессов. Многочисленные исследования учёных показали, что создать строгую теорию турбулентного режима не представляется возможным, поэтому для теоретических и инженерных расчётов пользуются экспериментальными данными, графическими зависимостями и эмпирическими формулами.
Как отмечено выше, при числах Рейнольдса Re

В результате сложного характера движения частиц жидкости в турбулентном потоке в любой его точке в каждый момент времени мгновенная скорость может принимать новые значения по величине и направлению. Эти колебания во времени мгновенной местной скоро­сти называются пульсацией скорости. Пульсация скорости сопровож­дается пульсацией давления.
Величина скорости беспорядочно колеблется около некоторого осредненного по времени значения U, которое в данном случае оста­ется постоянным.
Для упрощения расчетов вводится понятие «средняя местная ско­рость U». Это фиктивная средняя скорость в данной точке потока за достаточно длинный промежуток времени.
Эта скорость, как показы­вают опыты, несмотря на значительные колебания мгновенных ско­ростей, остается практически постоянной и параллельной оси потока.
Это позволяет применять для турбулентных потоков уравнение Бернулли.

Пример 2: Определить мощность, необходимую для работы центро­бежного насоса, установленного по схеме, изображённой на рисунке. Насос перекачивает жидкость удельного веса γ = 900 кГ/м3 из открытого резервуара А в напорный резервуар В, разность уров­ней в которых Н=20 м. В резервуаре В поддерживается избыточное давление рв=1,2 ати. Производительность насо­са Q = 50 л/сек, его коэффициент полезного действия η = 0,8 потери напора во всасывающем и нагнетательном трубопрово­дах hA-B=8 м.
Решение: Составляем уравнение Бернулли для сечений 1 и 2, совпадаю­щих со свободными поверхностями жидкости в резервуарах А и В. При этом следует учесть, что напор в сечении 2 будет боль­ше, чем напор в сечении 1, на величину напора Нн, развиваемого насосом и сообщаемого им жидкости, и меньше на потерю напора hA-B между этими сечениями. Таким образом, имеем:

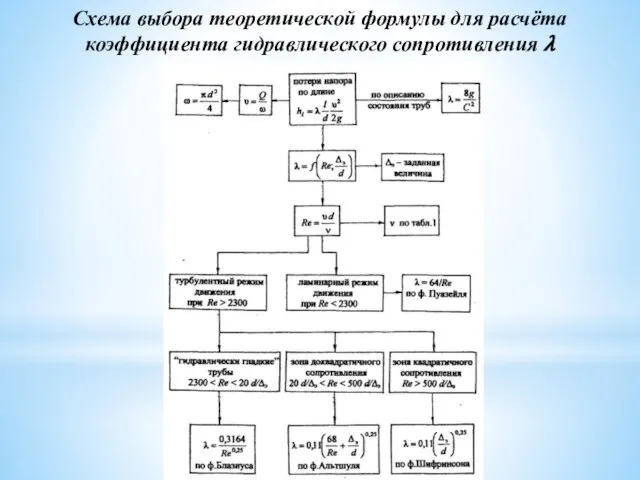
Схема выбора теоретической формулы для расчёта коэффициента гидравлического сопротивления ?

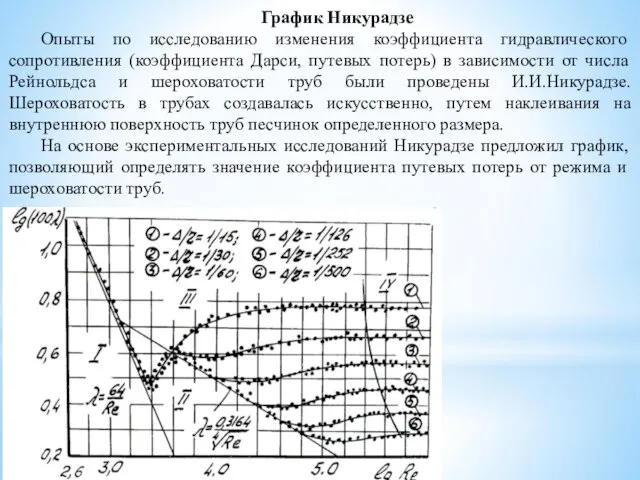
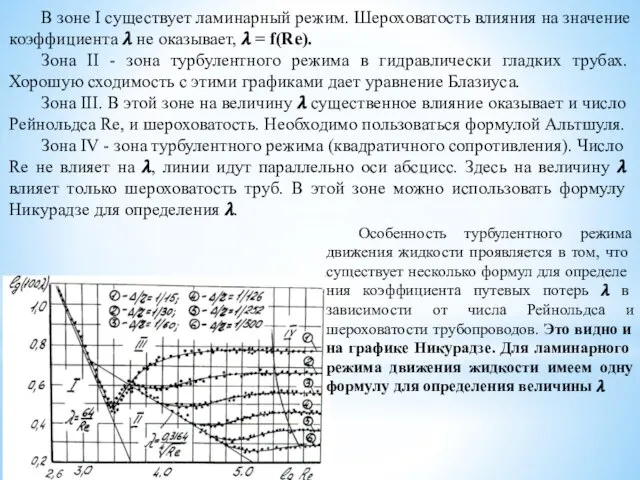
График Никурадзе
Опыты по исследованию изменения коэффициента гидравличе­ского сопротивления (коэффициента Дарси, путевых потерь) в зави­симости от числа Рейнольдса и шероховатости труб были проведены И.И.Никурадзе. Шероховатость в трубах создавалась искусственно, путем наклеивания на внутреннюю поверхность труб песчинок опре­деленного размера.
На основе экспериментальных исследований Никурадзе предло­жил график, позволяющий определять значение коэффици­ента путевых потерь от режима и шероховатости труб.

В зоне I существует ламинарный режим. Шероховатость влияния на значение коэффициента ? не оказывает, ? = f(Re).
Зона II - зона турбулентного режима в гидравлически гладких трубах. Хорошую сходимость с этими графиками дает уравнение Блазиуса.
Зона III. В этой зоне на величину ? существенное влияние оказы­вает и число Рейнольдса Rе, и шероховатость. Необходимо пользо­ваться формулой Альтшуля.
Зона IV - зона турбулентного режима (квадратичного сопротив­ления). Число Rе не влияет на ?, линии идут параллельно оси абс­цисс. Здесь на величину ? влияет только шероховатость труб. В этой зоне можно использовать формулу Никурадзе для определения ?.
Особенность турбулентного режима движения жидкости про­является в том, что существует несколько формул для определе­ния коэффициента путевых потерь ? в зависимости от числа Рейнольдса и шероховатости трубопроводов. Это видно и на гра­фике Никурадзе. Для ламинарного режима движения жидкости имеем одну формулу для определения величины ?