Введение в гидродинамику

Лекции по гидродинамике Часть 1
Гидродинамика изучает законы движения жидкостей и рассматривает приложения этих законов к решению практических инженерных задач

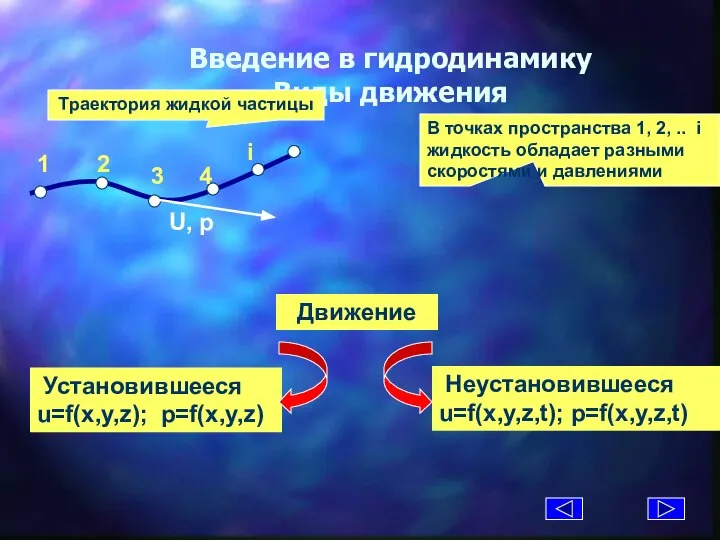
Введение в гидродинамику
Виды движения
Траектория жидкой частицы
В точках пространства 1, 2, .. i жидкость обладает разными скоростями и давлениями
Движение

Элементарная струйка и поток жидкости
Поток жидкости – совокупность элементарных струек, движущихся с разными скоростями
Живое (поперечное) сечение – сечение, перпендикулярное направлению скоростей
S=πd2/4
-площадь сечения
Π=πd
-смоченный периметр

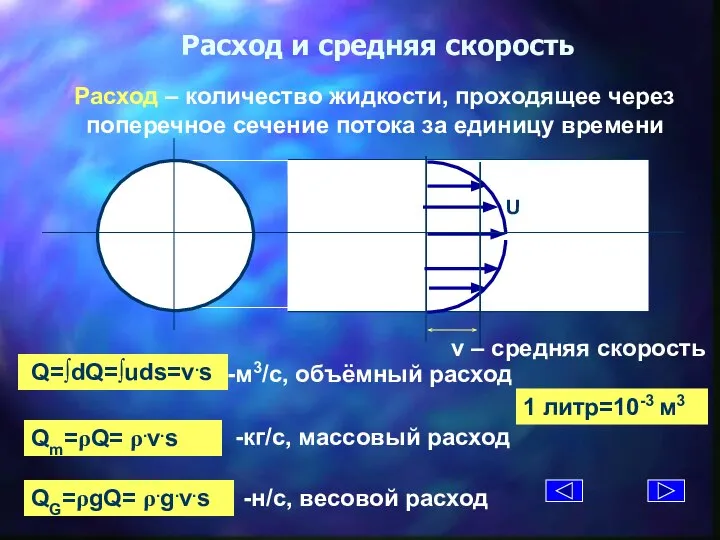
Расход и средняя скорость
Расход – количество жидкости, проходящее через поперечное сечение потока за единицу времени
Q=∫dQ=∫uds=v.s
-м3/с, объёмный расход
Qm=ρQ= ρ.v.s
-кг/c, массовый расход
QG=ρgQ= ρ.g.v.s
-н/c, весовой расход
1 литр=10-3 м3

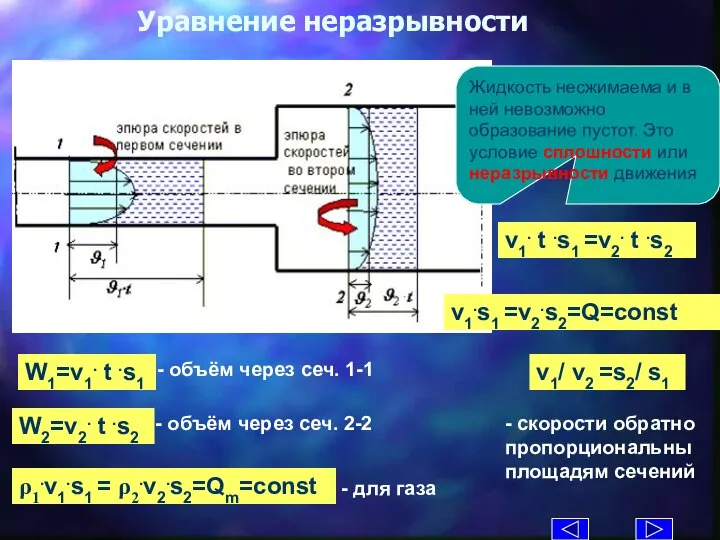
Уравнение неразрывности
W1=v1. t .s1
- объём через сеч. 1-1
v1. t .s1 =v2. t .s2
W2=v2. t .s2
- объём через сеч. 2-2
Жидкость несжимаема и в ней невозможно образование пустот. Это условие сплошности или неразрывности движения
v1.s1 =v2.s2=Q=const
v1/ v2 =s2/ s1
- скорости обратно пропорциональны площадям сечений
ρ1.v1.s1 = ρ2.v2.s2=Qm=const
- для газа

Энергия и работа
Энергия
Энергия – это невостребованная работа, математическая абстракция, формула, по которой можно вычислить максимальную работу
Определяет запас работы, которую может совершить тело, изменяя свое состояние
η = работа / энергия=A / E
- к.п.д. механизма
Работа
Скалярное произведение силы на перемещение под действием этой силы. A=F . s . cos a

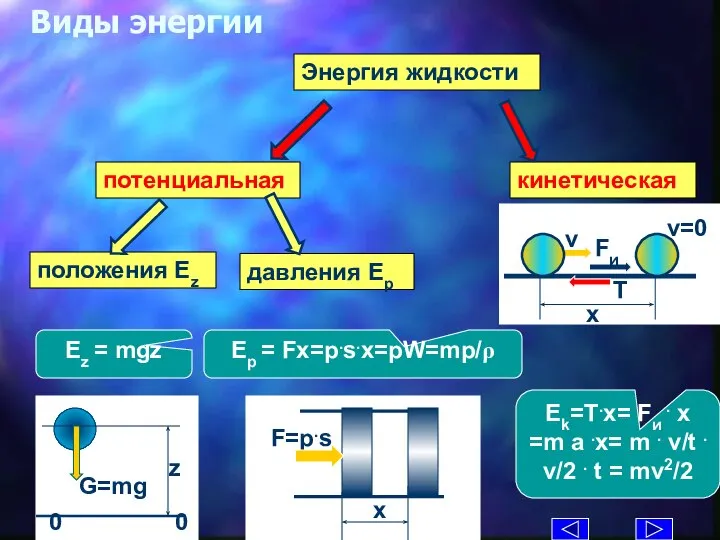
Виды энергии
Энергия жидкости
Ez = mgz
Ep = Fx=p.s.x=pW=mp/ρ
Ek=T.x= Fи . x =m a .x= m . v/t . v/2 . t = mv2/2

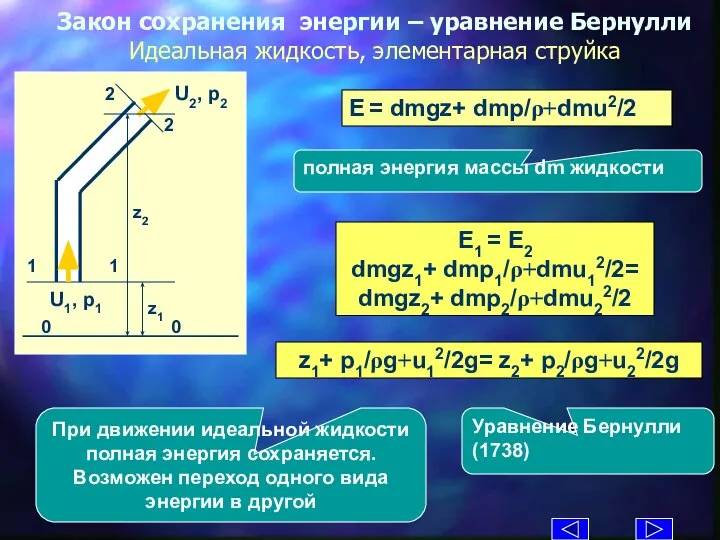
Закон сохранения энергии – уравнение Бернулли
Идеальная жидкость, элементарная струйка
E = dmgz+ dmp/ρ+dmu2/2
полная энергия массы dm жидкости
При движении идеальной жидкости полная энергия сохраняется. Возможен переход одного вида энергии в другой
E1 = E2
dmgz1+ dmp1/ρ+dmu12/2=
dmgz2+ dmp2/ρ+dmu22/2
z1+ p1/ρg+u12/2g= z2+ p2/ρg+u22/2g
Уравнение Бернулли (1738)

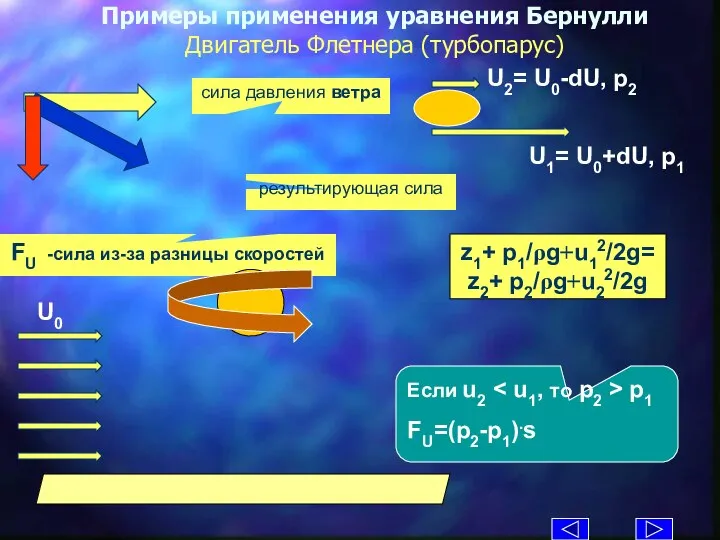
Примеры применения уравнения Бернулли
Двигатель Флетнера (турбопарус)
z1+ p1/ρg+u12/2g= z2+ p2/ρg+u22/2g
Если u2 < u1, то р2 > p1
FU=(p2-p1).s
сила давления ветра
FU -сила из-за разницы скоростей
результирующая сила

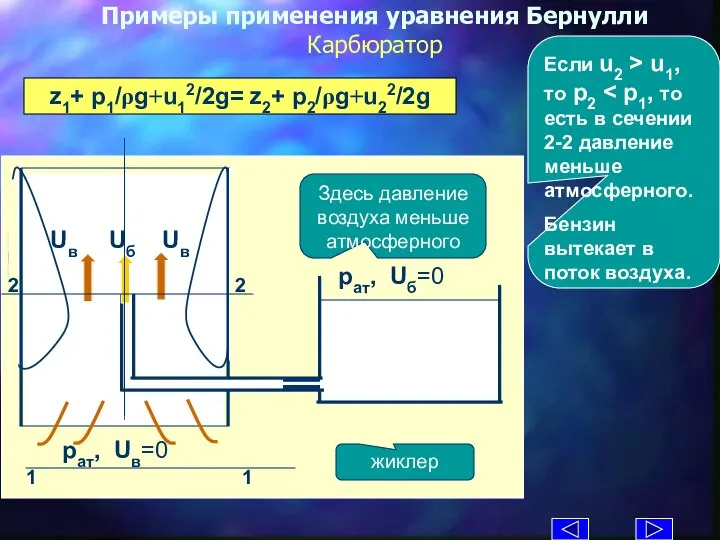
Примеры применения уравнения Бернулли
Карбюратор
z1+ p1/ρg+u12/2g= z2+ p2/ρg+u22/2g
жиклер
Здесь давление воздуха меньше атмосферного
Если u2 > u1, то р2 < p1, то есть в сечении 2-2 давление меньше атмосферного.
Бензин вытекает в поток воздуха.

Кинетическая энергия потока жидкости
Ek = ∫dmu2/2=αmv2/2
Кинетическая энергия массы m потока жидкости – сумма энергий отдельных струек
Коэффициент Кориолиса α - отношение действительной кинетической энергии к энергии, определяемой по средней скорости
Чем больше неравномерность скоростей u, тем больше α. Для ламинарного режима α=2, для турбулентного α=1,1−1,2 (на практике принимается 1).

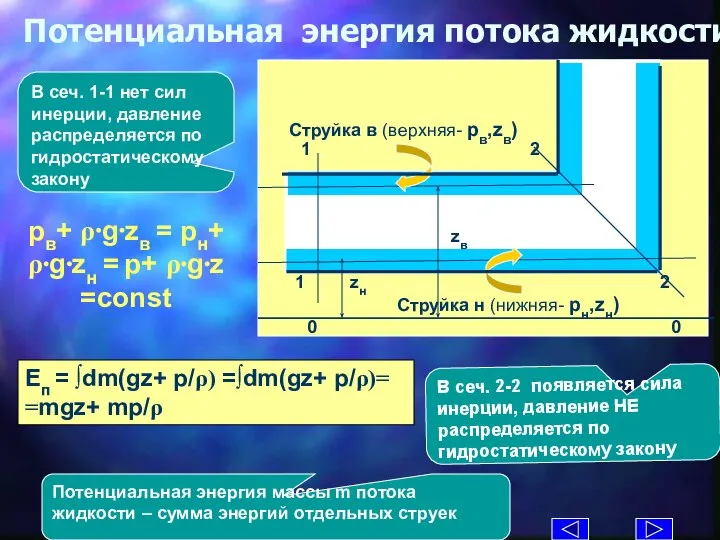
Потенциальная энергия потока жидкости
Eп = ∫dm(gz+ p/ρ) =∫dm(gz+ p/ρ)= =mgz+ mp/ρ
Потенциальная энергия массы m потока жидкости – сумма энергий отдельных струек
pв+ ρ⋅g⋅zв = pн+ ρ⋅g⋅zн = p+ ρ⋅g⋅z =const
В сеч. 1-1 нет сил инерции, давление распределяется по гидростатическому закону
В сеч. 2-2 появляется сила инерции, давление НЕ распределяется по гидростатическому закону

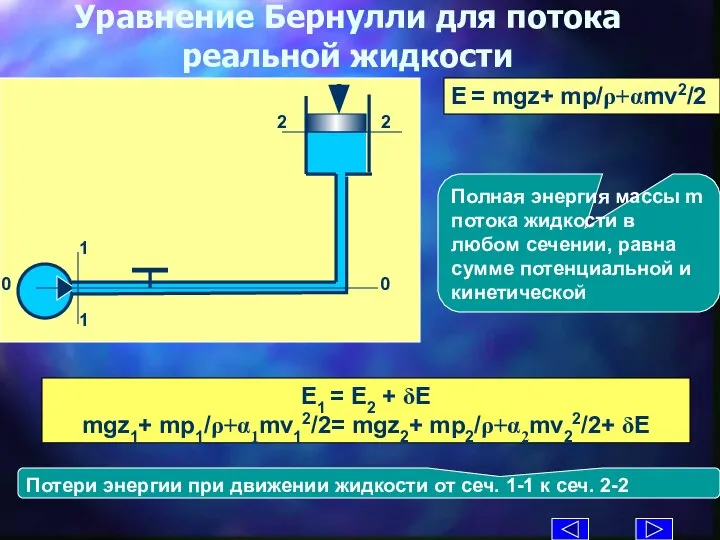
Уравнение Бернулли для потока реальной жидкости
E = mgz+ mp/ρ+αmv2/2
E1 = E2 + δE
mgz1+ mp1/ρ+α1mv12/2= mgz2+ mp2/ρ+α2mv22/2+ δE
Потери энергии при движении жидкости от сеч. 1-1 к сеч. 2-2
Полная энергия массы m потока жидкости в любом сечении, равна сумме потенциальной и кинетической

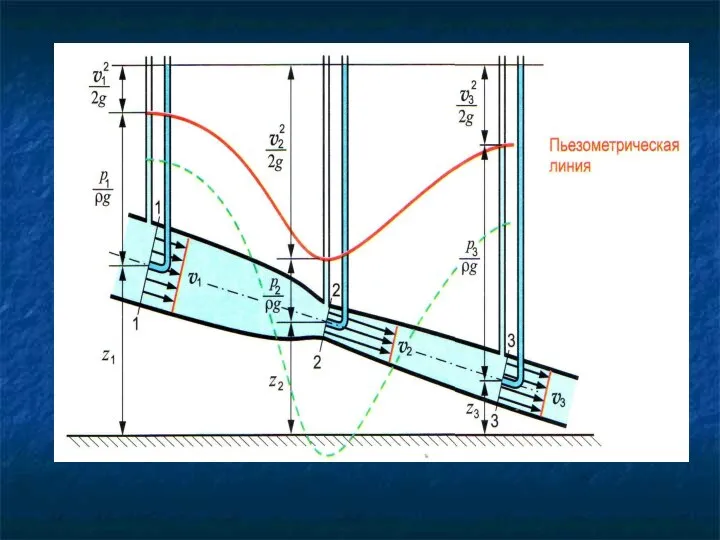
E/G =E/mg = z+ p/ρg+αv2/2g=H
УДЕЛЬНАЯ - энергия, отнесенная к количеству вещества (объёмному, или массовому, или весовому)
E/W =E/(m/ρ) = ρgz+ p+αρv2/2
E = mgz+ mp/ρ+αmv2/2
Полная энергия, джоули (Н*м)
Удельная энергия

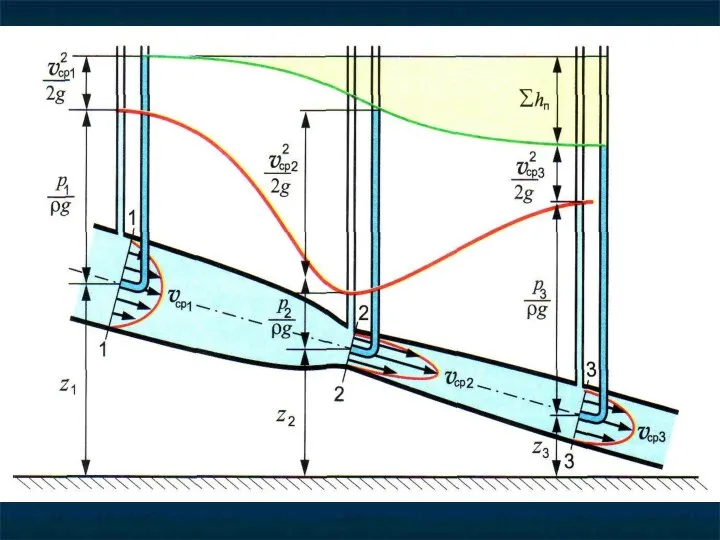
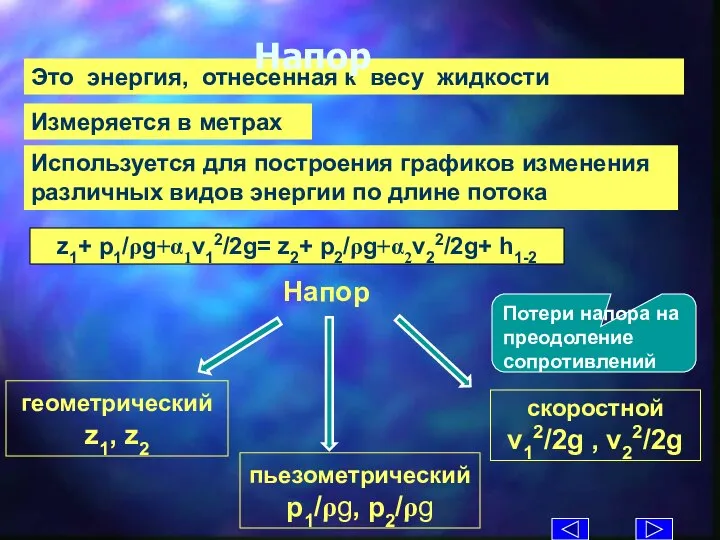
z1+ p1/ρg+α1v12/2g= z2+ p2/ρg+α2v22/2g+ h1-2
Это энергия, отнесенная к весу жидкости
Напор
Измеряется в метрах
Используется для построения графиков изменения различных видов энергии по длине потока
Напор
Потери напора на преодоление сопротивлений

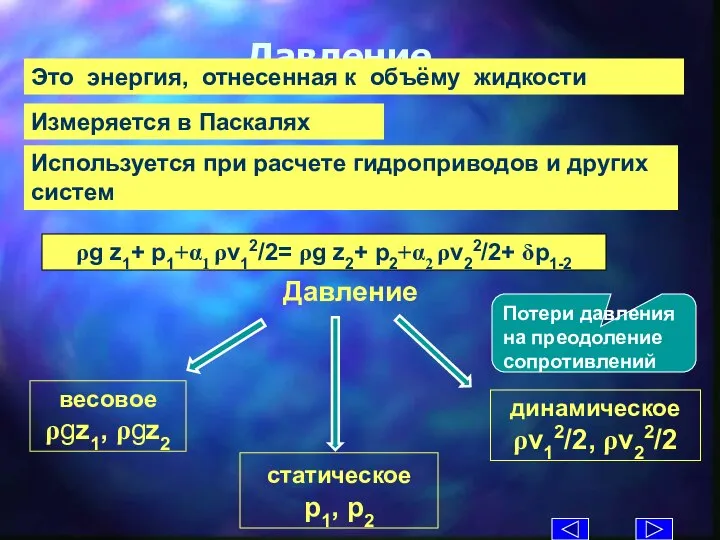
ρg z1+ p1+α1 ρv12/2= ρg z2+ p2+α2 ρv22/2+ δp1-2
Давление
Это энергия, отнесенная к объёму жидкости
Измеряется в Паскалях
Используется при расчете гидроприводов и других систем
Давление
Потери давления на преодоление сопротивлений

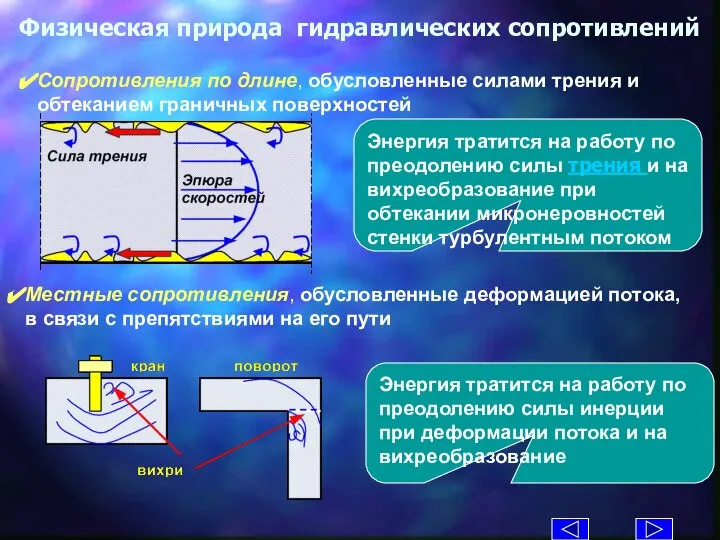
Физическая природа гидравлических сопротивлений
Местные сопротивления, обусловленные деформацией потока, в связи с препятствиями на его пути
Сопротивления по длине, обусловленные силами трения и обтеканием граничных поверхностей
Энергия тратится на работу по преодолению силы трения и на вихреобразование при обтекании микронеровностей стенки турбулентным потоком
Энергия тратится на работу по преодолению силы инерции при деформации потока и на вихреобразование

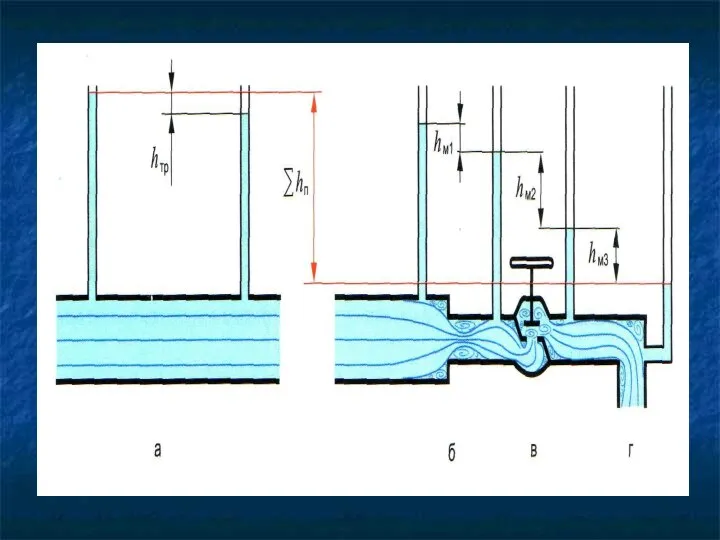
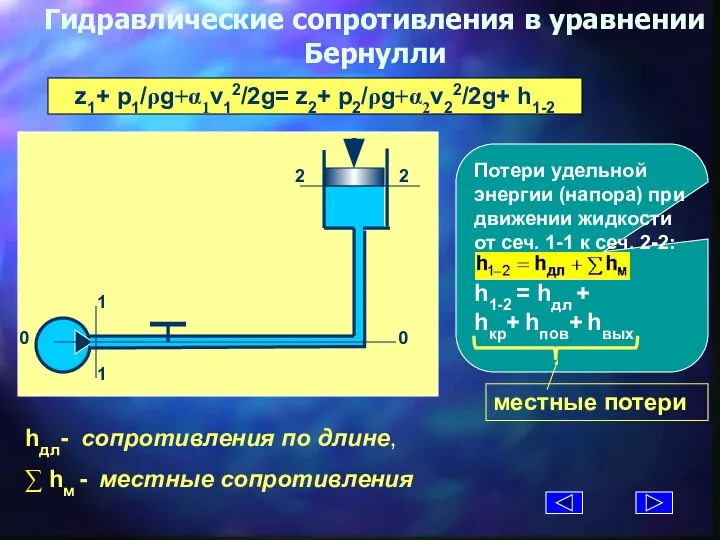
Гидравлические сопротивления в уравнении Бернулли
hдл- cопротивления по длине,
∑ hм - местные сопротивления
z1+ p1/ρg+α1v12/2g= z2+ p2/ρg+α2v22/2g+ h1-2

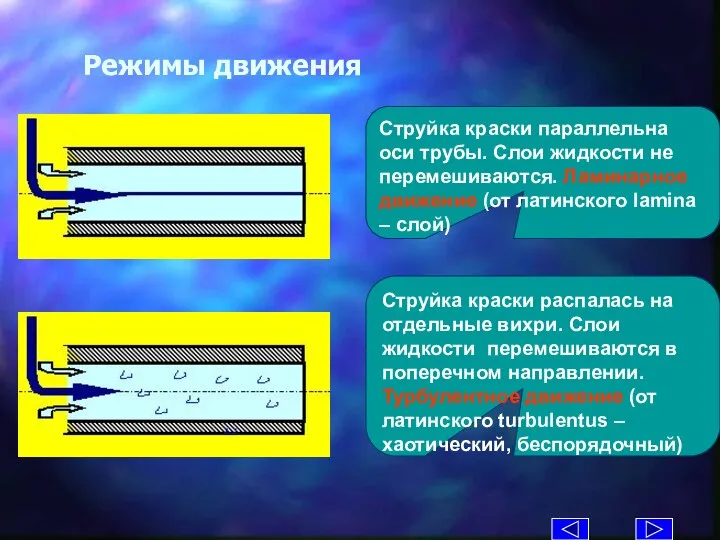
Режимы движения
Струйка краски параллельна оси трубы. Слои жидкости не перемешиваются. Ламинарное движение (от латинского lamina – слой)
Струйка краски распалась на отдельные вихри. Слои жидкости перемешиваются в поперечном направлении. Турбулентное движение (от латинского turbulentus – хаотический, беспорядочный)

Число Рейнольдса Re
Число (критерий) Рейнольдса). Re-мера отношения силы инерции к силе трения
- динамический коэффициент вязкости
- кинематический коэффициент вязкости
При увеличении скорости растут силы инерции. Силы трения при этом больше сил инерции и до некоторых пор выпрямляют траектории струек
При некоторой скорости vкр:
Сила инерции Fи > силы трения Fтр, поток становится турбулентным

Критическое число Рейнольдса Reкр
Число Рейнольдса, при котором ламинарный режим сменяется турбулентным
Reкр зависит от формы сечения канала
Reкр =2300
Reкр =1600

Гидравлический диаметр
Характерный линейный размер сечения.
S - площадь сечения; П - смоченный периметр

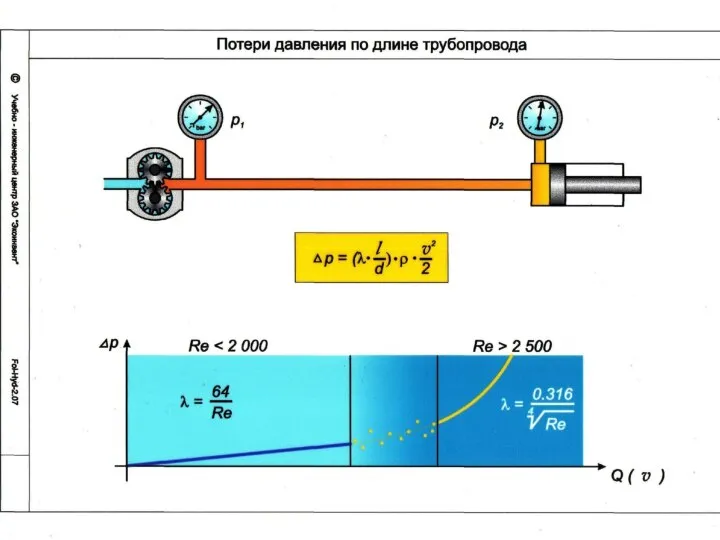
Потери по длине.
Формула Дарси-Вейсбаха
Формула Дарси-Вейсбаха
λ - коэффициент гидравлического трения, зависит от режима движения и состояния поверхности трубопровода
l, d – длина и диаметр трубопровода
v – средняя скорость движения

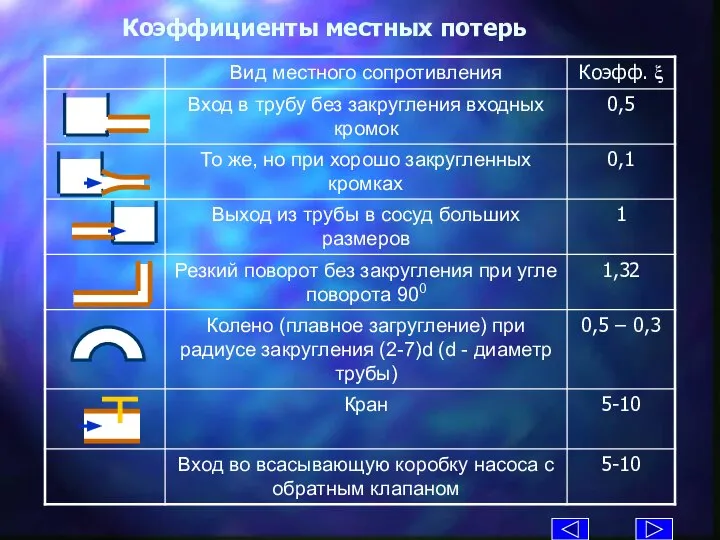
Местные потери. Формула Вейсбаха
Формула Вейсбаха
ξ - коэффициент местного сопротивления, зависит от его вида и конструктивного выполнения
ξ– приводится в справочной литературе
v – средняя скорость движения

Коэффициенты местных потерь

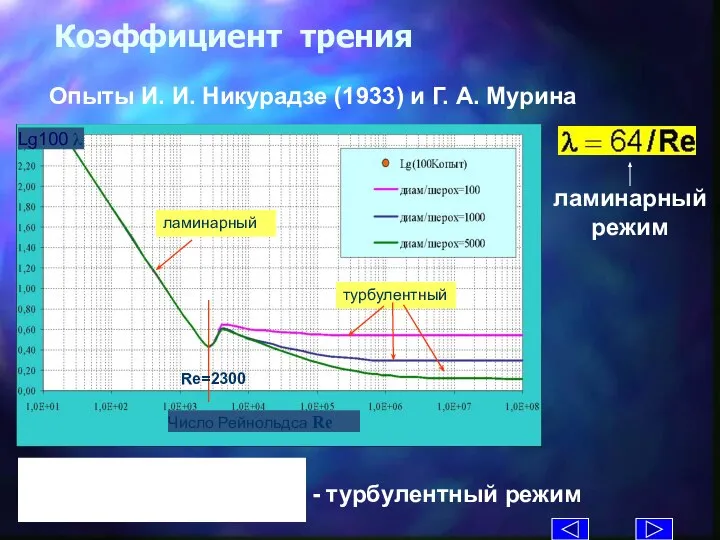
Lg100 λ
Коэффициент трения
Опыты И. И. Никурадзе (1933) и Г. А. Мурина
Число Рейнольдса Re

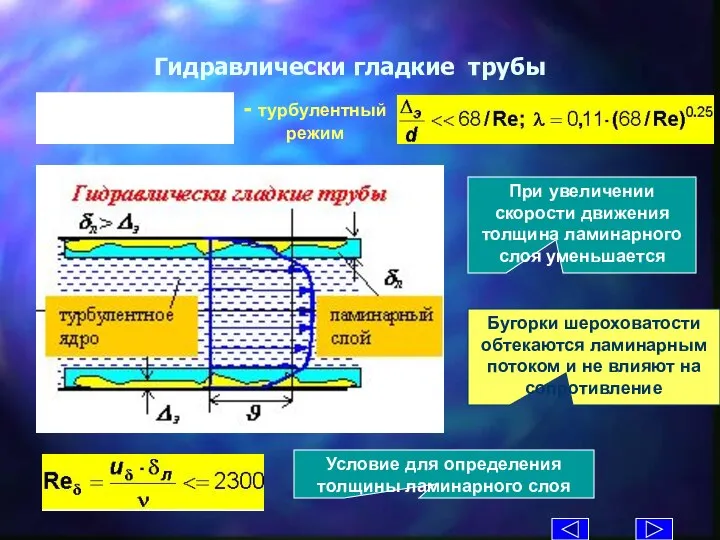
Гидравлически гладкие трубы
При увеличении скорости движения толщина ламинарного слоя уменьшается
Условие для определения толщины ламинарного слоя
Бугорки шероховатости обтекаются ламинарным потоком и не влияют на сопротивление

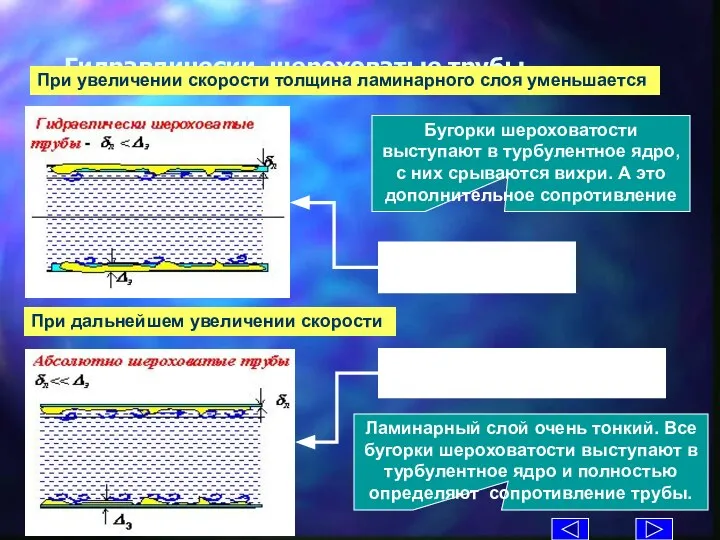
Гидравлически шероховатые трубы
Бугорки шероховатости выступают в турбулентное ядро, с них срываются вихри. А это дополнительное сопротивление
Ламинарный слой очень тонкий. Все бугорки шероховатости выступают в турбулентное ядро и полностью определяют сопротивление трубы.
При увеличении скорости толщина ламинарного слоя уменьшается
При дальнейшем увеличении скорости

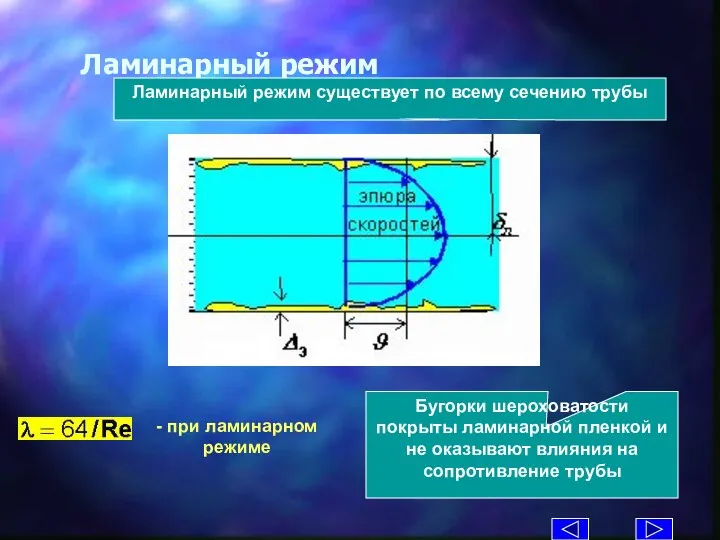
Ламинарный режим
Бугорки шероховатости покрыты ламинарной пленкой и не оказывают влияния на сопротивление трубы
Ламинарный режим существует по всему сечению трубы

Рекомендации для расчетов
- при ламинарном режиме
- при турбулентном режиме
При проведении расчетов то слагаемое, которое несущественно, дает незначительный вклад в величину коэффициента трения

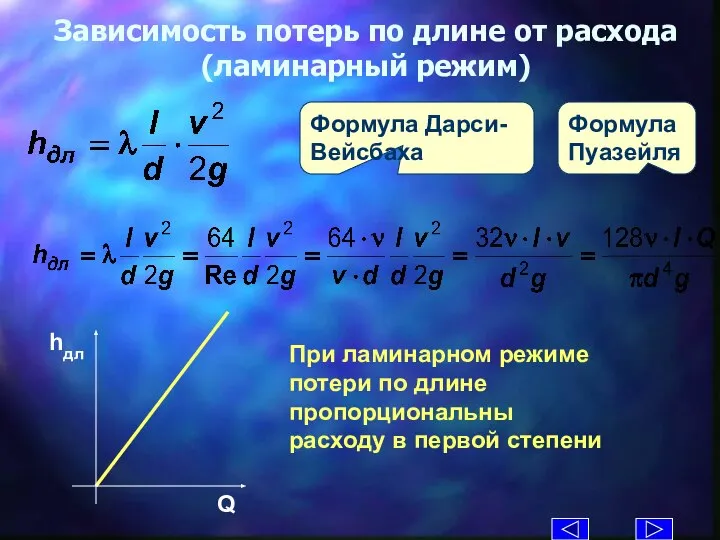
Формула Дарси-Вейсбаха
Зависимость потерь по длине от расхода (ламинарный режим)
Формула Пуазейля
При ламинарном режиме потери по длине пропорциональны расходу в первой степени