Содержание
- 2. ЛЕКЦИЯ 2 ВОЛНЫ *
- 3. Волны Волной называется распространение колебаний в пространстве Виды волн: 1- Механические ( упругие, звуковые)- распространение механических
- 4. 1. Механические волны * Источник механических волн – тело, совершающее колебательное движение, находясь в упругой среде.
- 5. Любой малый элемент твердого тела обладает массой и упругостью. В простейшей одномерной модели твердое тело можно
- 6. Частички среды совершают такие же колебания что и источник, но в другой фазе. Волна переносит энергию,
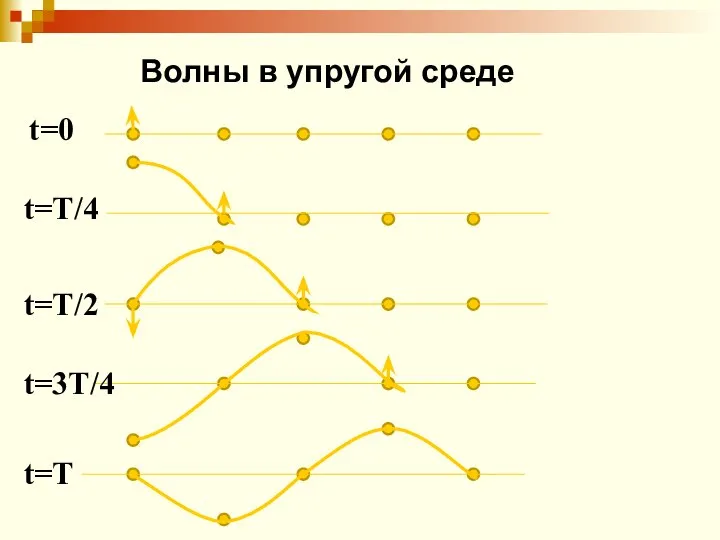
- 7. Волны в упругой среде t=0 t=T/4 t=T/2 t=3T/4 t=T
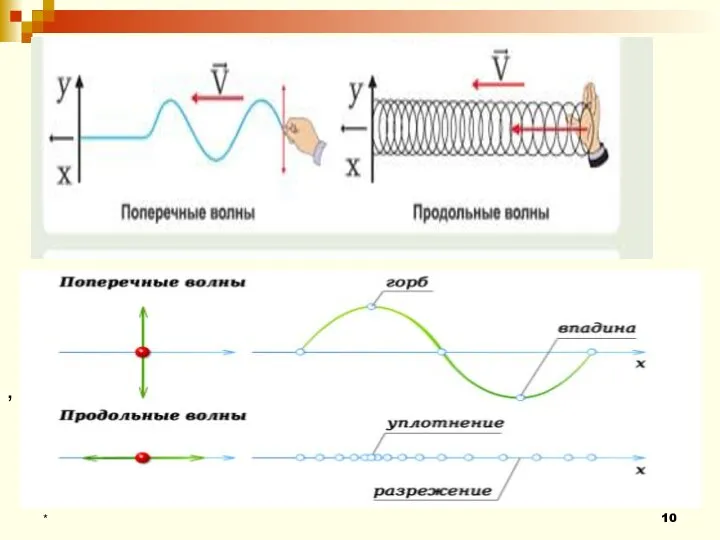
- 8. Волны можно классифицировать по разным признакам: 1. По направлению колебаний частиц среды. Поперечные волны – волны,
- 9. Продольные волны – частички среды колеблются вдоль направления распространения волны. Распространяются в твердых, жидких и газообразных
- 10. , *
- 11. В жидкостях или газах деформация сопровождается уплотнением или разрежением. Продольные механические волны могут распространяться в любых
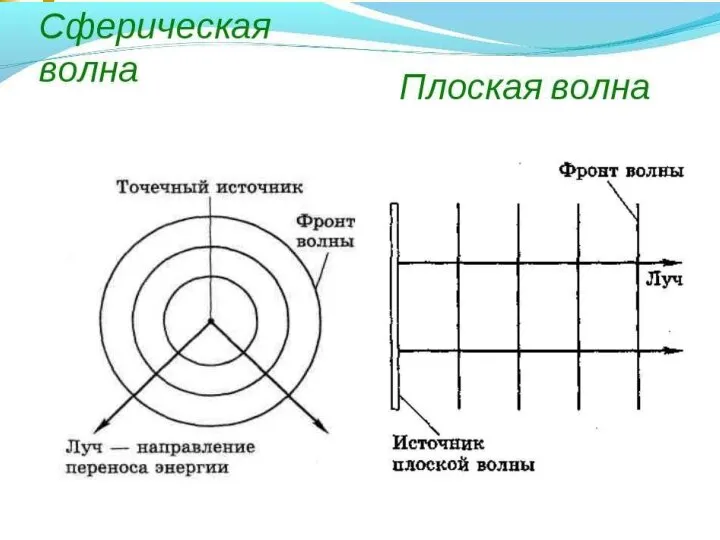
- 12. * 2. По форме волновой поверхности - сферические и плоские, цилиндрические и пр. На большом расстоянии
- 13. *
- 14. *
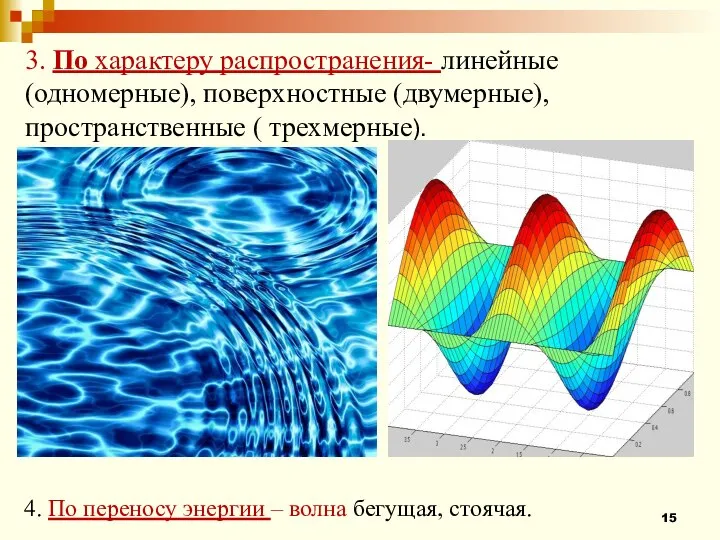
- 15. 3. По характеру распространения- линейные (одномерные), поверхностные (двумерные), пространственные ( трехмерные). 4. По переносу энергии –
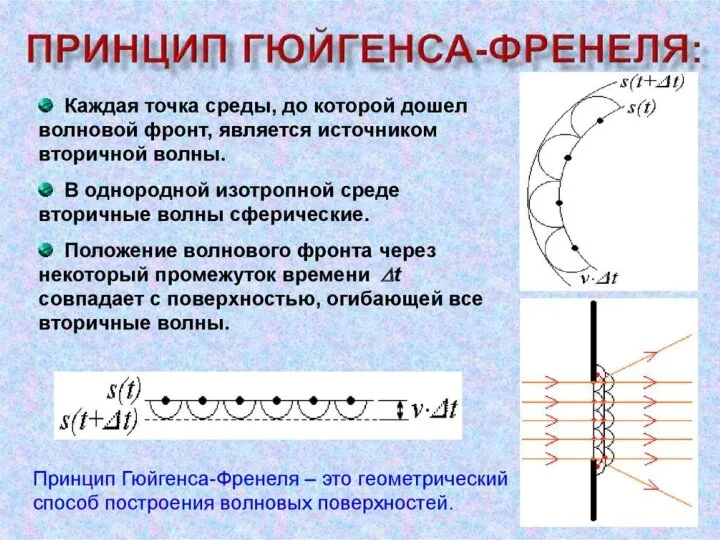
- 16. Общие сведения о волнах Несмотря на различную природу, механические и электромагнитные волны, как и колебания, подчиняются
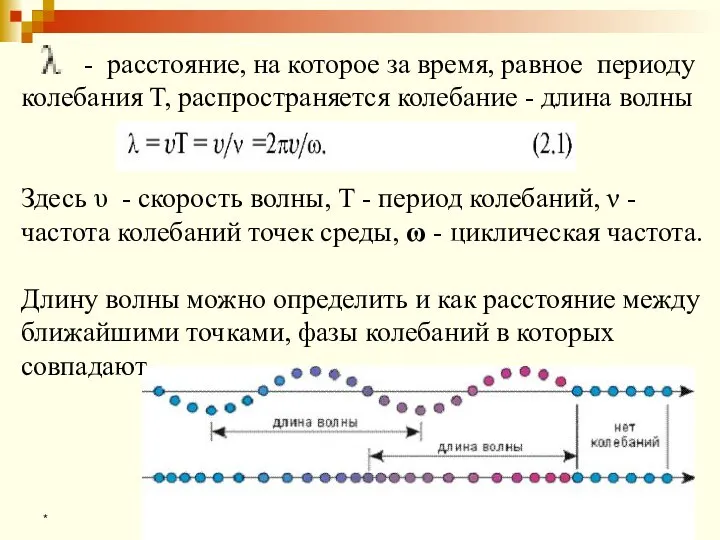
- 17. * - расстояние, на которое за время, равное периоду колебания Т, распространяется колебание - длина волны
- 18. Для характеристики волн, кроме длины волны , вводится циклическое волновое число k. Циклическое волновое число показывает,
- 19. БЕГУЩАЯ ВОЛНА * Пусть волна распространяется в направлении х в непоглощающей среде Ψ0 = A sin(ωt
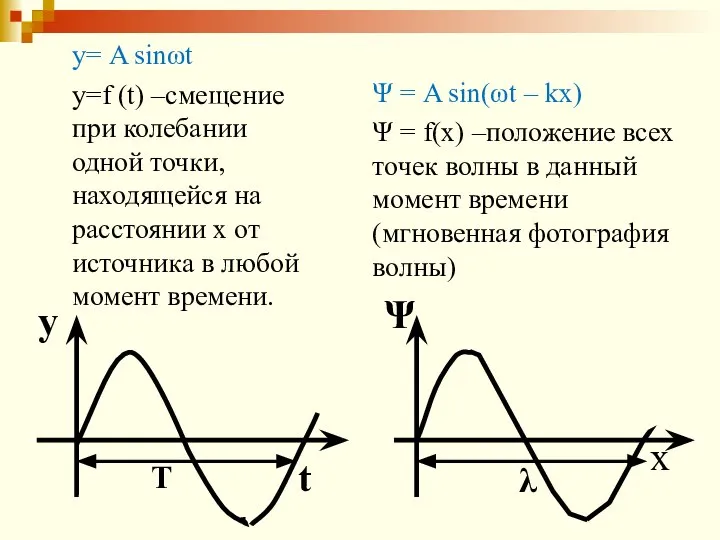
- 20. у= A sinωt у=f (t) –смещение при колебании одной точки, находящейся на расстоянии х от источника
- 21. Ψ – смещение точки, учасвующей в волновом процессе, от положения равновесия; φ= (ωt – kх)- фаза
- 22. * Для волны с данной λ при переходе из среды в среду сохраняется ω, Т, ν,
- 23. ВОЛНОВОЕ УРАВНЕНИЕ * Распространение волн в однородной среде в общем случае описывается волновым уравнением – дифференциальным
- 24. Фазовая скорость – это скорость распространения фазы волны. d Ψ / dt = υ * –
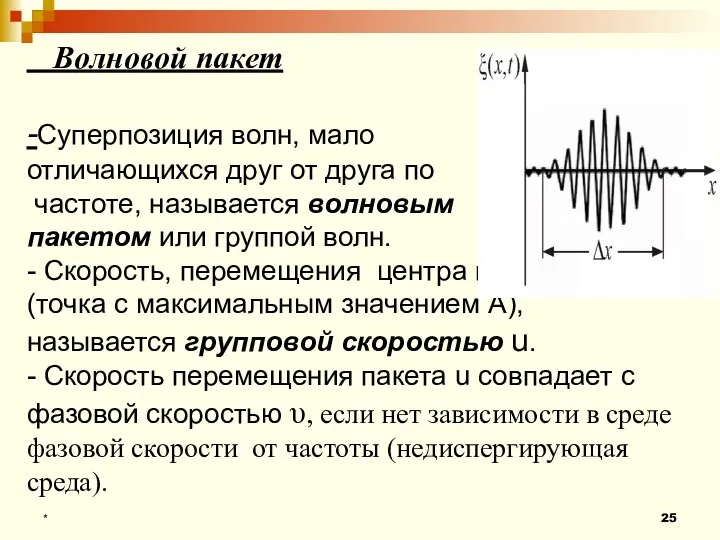
- 25. Волновой пакет -Суперпозиция волн, мало отличающихся друг от друга по частоте, называется волновым пакетом или группой
- 26. * За скорость распространения волнового пакета принимают скорость максимума амплитуды, т.е. центра пакета: υ =ω/k- фазовая
- 27. ЭНЕРГЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ВОЛН 1. Поток энергии – количество энергии, переносимое волной за единицу времени через некоторую
- 28. потока энергии – энергия, переносимая волной через единичную площадку за единицу времени 4. Интенсивность волны –
- 29. * Энергия волны Упругая среда, в которой распространяются механические волны, обладает кинетической энергией колеблющихся частиц Wk
- 30. * Относительная деформация ε =dΨ/dx=Аkcos(ωt - kх), где Е- модуль Юнга, Е= υ2ρ Wп =Еε2/2 dWп
- 31. * Максимумы потенциальной энергии приходятся на те же области, где максимальна кинетическая энергия. Это особенность бегущих
- 32. Стоячая волна Если рассматривать бегущую волну, то в направлении ее распространения переносится энергия колебательного движения. В
- 33. Интерференция волн. Стоячие волны Интерференцией называется явление наложения когерентных волн, при котором происходит перераспределение энергии колебаний
- 34. * Важным случаем интерференции волн является наложение двух плоских бегущих волн одинаковой частоты, распространяющихся в противоположных
- 35. * В точках, координаты которых удовлетворяют условию А ст=2А амплитуда колебаний достигает максимального значения. Эти точки
- 36. * В точках, координаты которых удовлетворяют условию амплитуда колебаний обращается в нуль (А ст=0) . Эти
- 37. * . Все точки, заключенные между двумя соседними узлами, колеблются синфазно (т.е. в одинаковой фазе). ∆φ
- 38. Собственные колебания сплошной ограниченной среды Ограниченная среда- ( струна с закрепленными концами, стержень, труба с воздухом)-
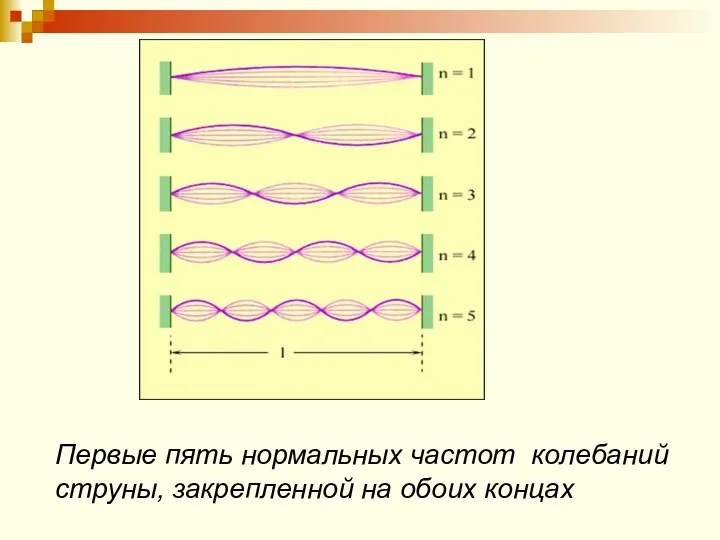
- 39. Колебания струны * В закрепленной с обоих концов натянутой струне при возбуждении поперечных колебаний устанавливаются стоячие
- 40. Этим длинам волны соответствуют частоты, которые Называются собственными частотами струны Собственные частоты являются кратными частоте ,
- 41. Спектр собственных частот колебаний струны Уравнение стоячей волны в струне с закрепленными концами На концах струны
- 42. Первые пять нормальных частот колебаний струны, закрепленной на обоих концах
- 43. Энергия стоячей волны * Формула объемной плотности кинетической энергии волны для стоячей волны имеет вид а
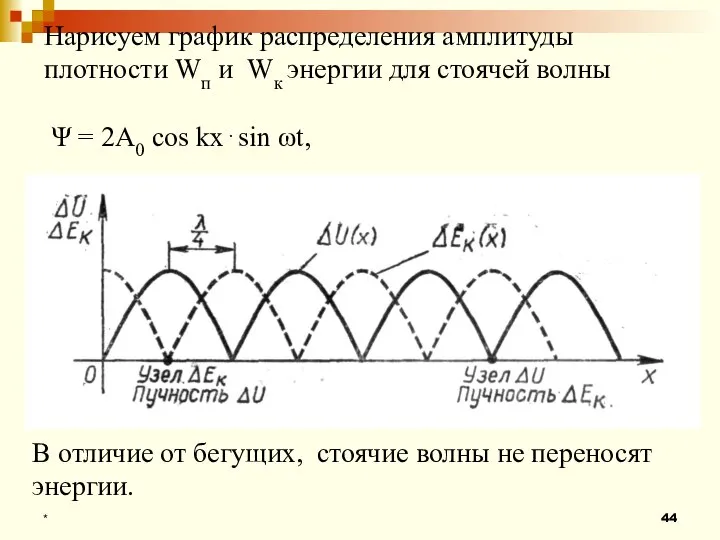
- 44. Нарисуем график распределения амплитуды плотности Wп и Wк энергии для стоячей волны Ψ = 2А0 cos
- 45. * В моменты когда Wк =0, Wп достигает максимального значения, т.е. Wп и Wк сдвинуты на
- 46. * Дважды за период Wк движущихся частиц переходит и Wп деформированных участков среды. Таким образом, стоячая
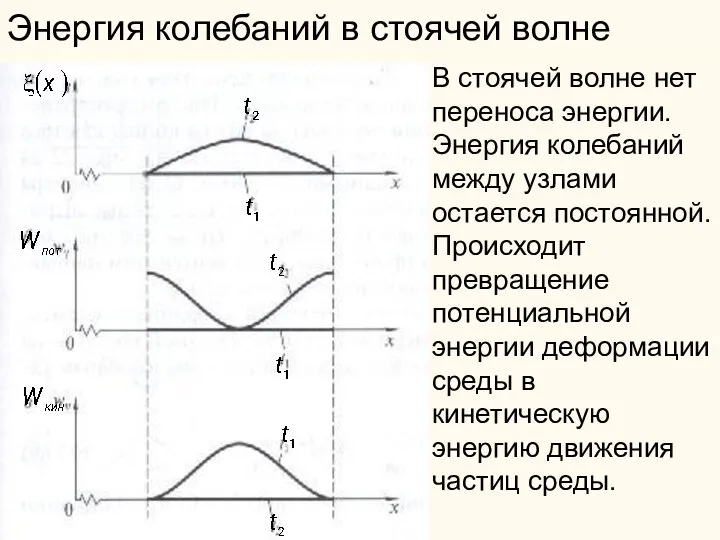
- 47. Энергия колебаний в стоячей волне В стоячей волне нет переноса энергии. Энергия колебаний между узлами остается
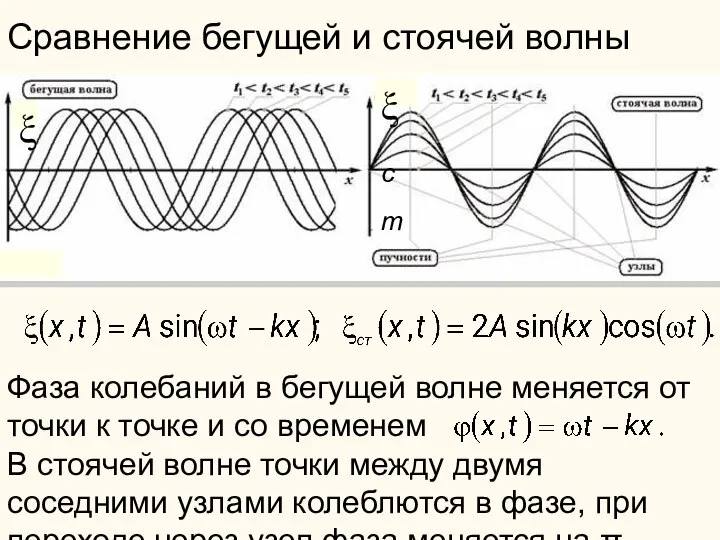
- 48. Сравнение бегущей и стоячей волны Фаза колебаний в бегущей волне меняется от точки к точке и
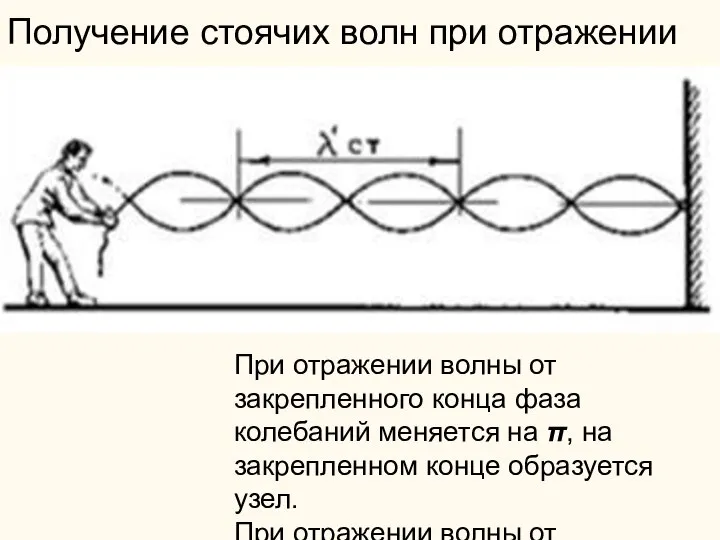
- 49. Получение стоячих волн при отражении При отражении волны от закрепленного конца фаза колебаний меняется на π,
- 50. 2.Электромагнитная волна * Условие возникновения э/м волны – наличие источника изменяющегося со временем э/м поля. Переменное
- 51. Пусть среда, в которой распространяются электромагнитные волны, однородная, нейтральная, непроводящая. *
- 52. *
- 53. Свойства электромагнитных волн. 1. Скорость распространения электромагнитных волн • Здесь ε и μ – диэлектрическая и
- 54. • среда влияет на распространение электромагнитных волн, они преломляются, отражаются, поглощаются. 2. Электромагнитная волна – поперечная,
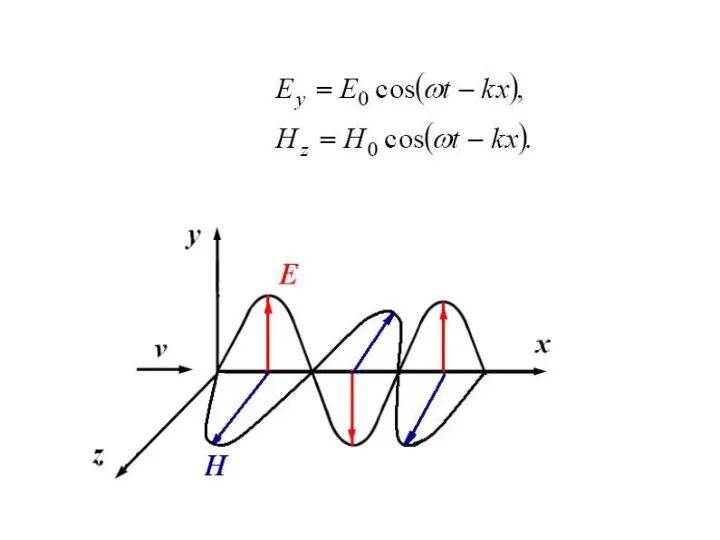
- 55. 4. Вектора Е и Н колеблются в одной фазе – одновременно обращаются в нуль и одновременно
- 56. *
- 57. * 6. Электромагнитная волна переносит энергию (электромагнитную волну можно обнаружить) 7. Электромагнитная волна оказывает на тело
- 58. Объемная плотность энергии э/м волны * - показывает какая энергия была бы сосредоточена в единице объема
- 59. Плотность потока энергии * равна объемной плотности энергии умноженной на скорость волны: j = S =ωv
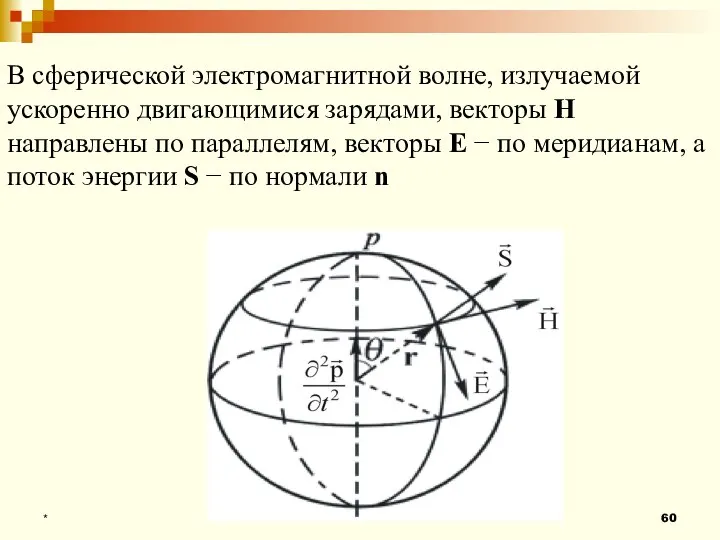
- 60. * В сферической электромагнитной волне, излучаемой ускоренно двигающимися зарядами, векторы Н направлены по параллелям, векторы Е
- 61. Электромагнитная масса и импульс * Электромагнитному полю присущи масса и электромагнитный импульс. p = mυ E
- 62. Излучение диполя * • Простейшая излучающая система –электрический диполь, дипольный момент pl которого изменяется с течением
- 63. *
- 64. Шкала электромагнитных волн * • В зависимости от частоты (или длины волны ), а так же
- 65. Радиоволны *
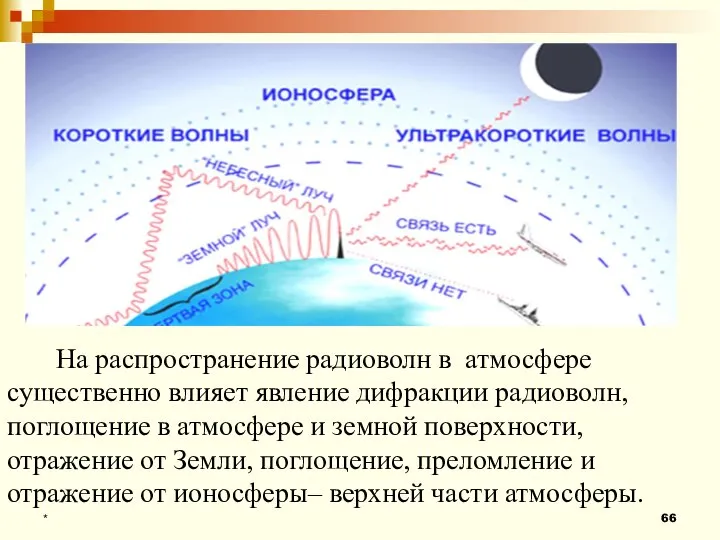
- 66. * На распространение радиоволн в атмосфере существенно влияет явление дифракции радиоволн, поглощение в атмосфере и земной
- 67. * Радиоволны (λ > 1 мм). Источниками радиоволн служат колебания зарядов в проводах, антеннах, колебательных контурах.
- 68. * • Дециметровые волны (10 см • Сантиметровые волны (1 см • Миллиметровые волны (1 мм
- 69. * . Радиосвязь–передача какой‐либо информации с помощью радиоволн. В радиовещании осуществляется передача речи, музыки, телеграфных сигналов.
- 70. * Средние и короткие волны радиоволны отражаются от слоѐв ионосферы, следовательно, возможна дальняя радиосвязь, могут обогнуть
- 71. Оптическое излучение: (СВЕТ) • инфракрасное излучение –электромагнитное излучение, испускаемое нагретыми телами, λ=1мм –770 нм. • видимое
- 72. * Ультрафиолетовое излучение (10 нм В небольших дозах ультрафиолетовое излучение полезно для человека: оно повышает иммунитет,
- 73. * Видимый свет (380 нм Излучение в этом промежутке длин волн воспринимается человеческим глазом. Диапазон видимого
- 74. * Инфракрасное излучение (780 нм Испускается молекулами и атомами нагретых тел. Инфракрасное излучение называется ещё тепловым
- 75. Рентгеновское излучение от 50 до 0,001 нм * –электромагнитное излучение, которое возникает при взаимодействии элементарных частиц
- 76. * Рентгеновское излучение (5 пм Возникает в результате торможения быстрых электронов у анода и стенок газоразрядных
- 77. Гамма‐излучение (гамма лучи) менее 0,01 нм. * Испускается возбуждѐнными атомными ядрами при радиоактивных превращениях и ядерных
- 79. Скачать презентацию



























































 Электромагнитные волны и их свойства
Электромагнитные волны и их свойства Законы геометрической оптики
Законы геометрической оптики Давление твердых тел. Способы уменьшения и увеличения давления
Давление твердых тел. Способы уменьшения и увеличения давления Complex numbers
Complex numbers Что изучает физика? Вводный урок в 7 классе
Что изучает физика? Вводный урок в 7 классе Колебания. Малые гармонические колебания
Колебания. Малые гармонические колебания Плотность. Расчет массы и объема тела по его плотности
Плотность. Расчет массы и объема тела по его плотности Игра К вершинам физики
Игра К вершинам физики Относительность движения
Относительность движения Презентация на тему Возможно ли создать электричество дома
Презентация на тему Возможно ли создать электричество дома  Презентация на тему газовые законы
Презентация на тему газовые законы  Закон всемирного тяготения. Исаак Ньютон
Закон всемирного тяготения. Исаак Ньютон Изобретение радио Поповым
Изобретение радио Поповым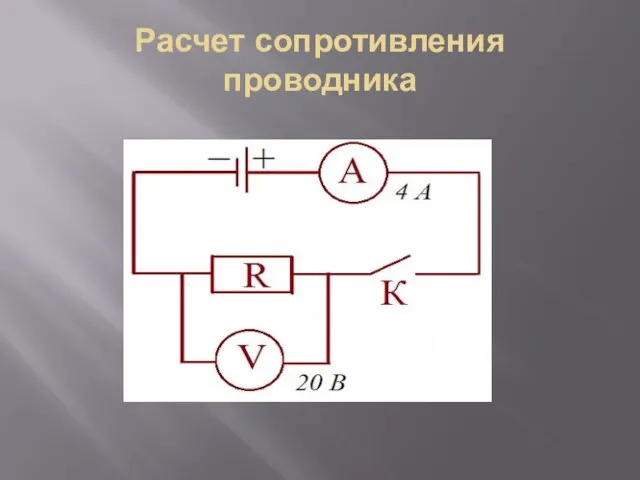 Расчет сопротивления проводника
Расчет сопротивления проводника Автоколебания. Транзистор. Генератор незатухающих колебаний
Автоколебания. Транзистор. Генератор незатухающих колебаний Решение задач на вычисление массы продукта реакции по известной массе исходного вещества, содержащего примеси
Решение задач на вычисление массы продукта реакции по известной массе исходного вещества, содержащего примеси Предыстория радиотехники. Лекция 3
Предыстория радиотехники. Лекция 3 Точечные дефекты
Точечные дефекты Закон Ома. Розв’язування задач
Закон Ома. Розв’язування задач Сила Архимеда – выталкивающая сила
Сила Архимеда – выталкивающая сила Подготовка к ОГЭ, физика 8 класс
Подготовка к ОГЭ, физика 8 класс Тепловые процессы
Тепловые процессы Решение задач по теме Основы термодинамики
Решение задач по теме Основы термодинамики Организация доступной среды на воздушном транспорте
Организация доступной среды на воздушном транспорте Разработка систем аварийной посадки квадрокоптера
Разработка систем аварийной посадки квадрокоптера Наклонная плоскость
Наклонная плоскость Презентация на тему Модели строения газа, жидкости и твердого тела
Презентация на тему Модели строения газа, жидкости и твердого тела  Аксиомы статики
Аксиомы статики