Содержание
- 2. Напряженность и потенциал электростатического поля в проводнике В проводниках имеются электрически заряженные частицы – носители заряда
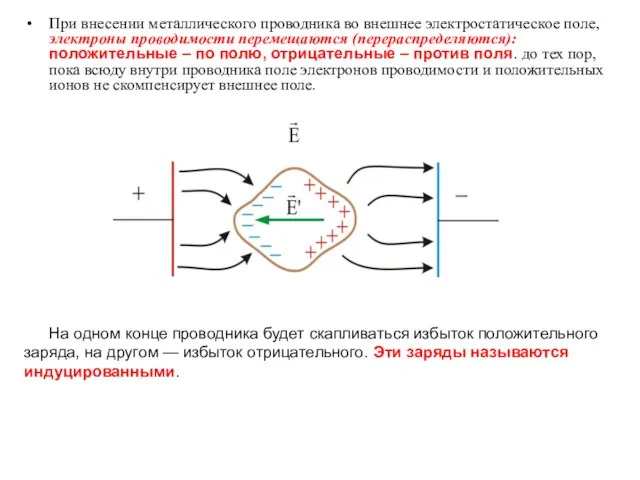
- 3. При внесении металлического проводника во внешнее электростатическое поле, электроны проводимости перемещаются (перераспределяются): положительные – по полю,
- 4. В установившимся состоянии в проводнике, помещенном в электростатическое поле мы имеем: Появление у заряженной поверхности на
- 5. Действительно, в любой точке внутри проводника, следовательно, φ = const. Поверхность проводника тоже эквипотенциальна: (для любой
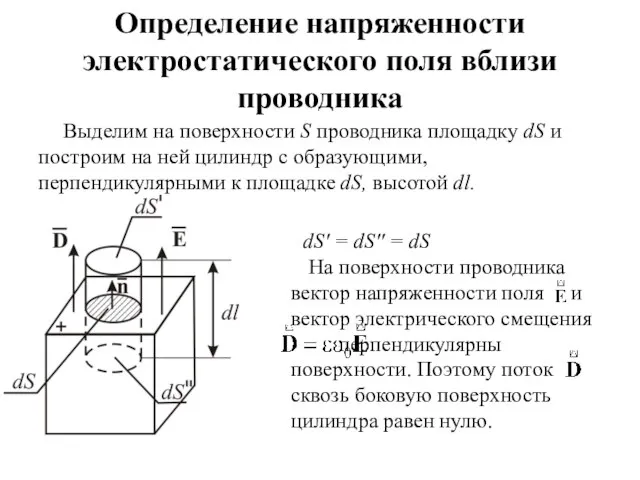
- 6. Определение напряженности электростатического поля вблизи проводника Выделим на поверхности S проводника площадку dS и построим на
- 7. Поток вектора электрического смещения через dS'' тоже равен нулю, так как dS'' лежит внутри проводника, где
- 8. В состоянии равновесия внутри проводника заряды отсутствуют, и создание внутри него полости не повлияет на конфигурацию
- 9. Конденсаторы Электрическая емкость. При сообщении проводнику заряда, на его поверхности появляется потенциал φ. Но если этот
- 10. Один фарад – это емкость такого проводника, потенциал которого изменяется на один вольт при сообщении ему
- 11. Электроемкость уединенного проводника зависит от его геометрических размеров, формы и диэлектрических свойств окружающей среды и не
- 12. Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на
- 13. Плоский конденсатор Плоский конденсатор состоит из двух параллельных пластин, площадью S каждая и находящихся на расстоянии
- 14. Из предыдущего слайда (путем замены знаков) имеем: Тогда: - емкость плоского конденсатора. Сферический конденсатор Сферический конденсатор
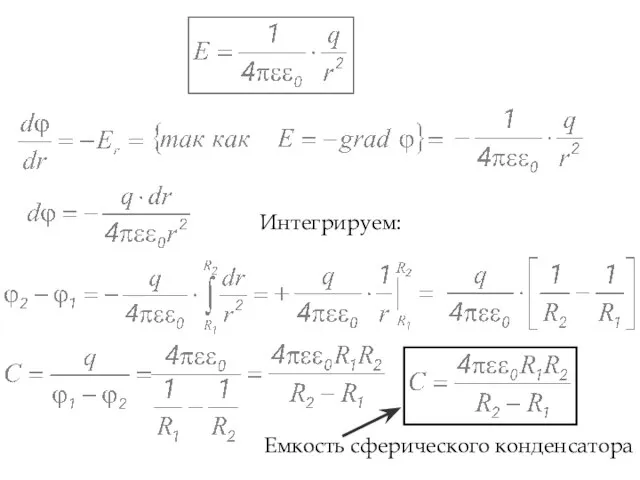
- 15. Интегрируем: Емкость сферического конденсатора
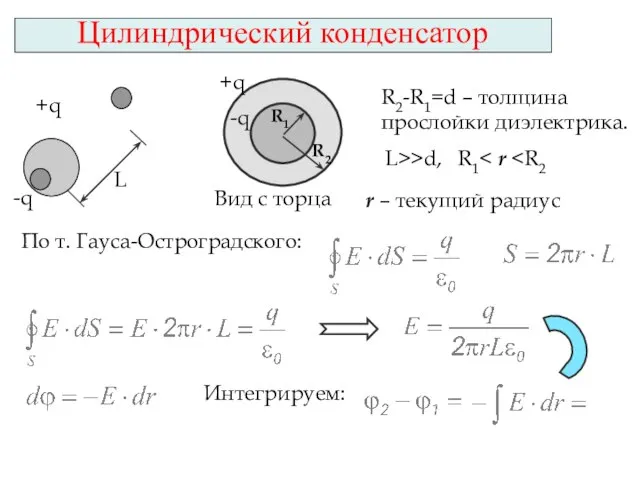
- 16. Цилиндрический конденсатор L +q -q +q -q R1 R2 Вид с торца R2-R1=d – толщина прослойки
- 17. Емкость цилиндрического конденсатора.
- 19. Последовательное и параллельное соединение конденсаторов Параллельное соединение: Для получения большей емкости конденсаторы соединяют параллельно. С1 С2
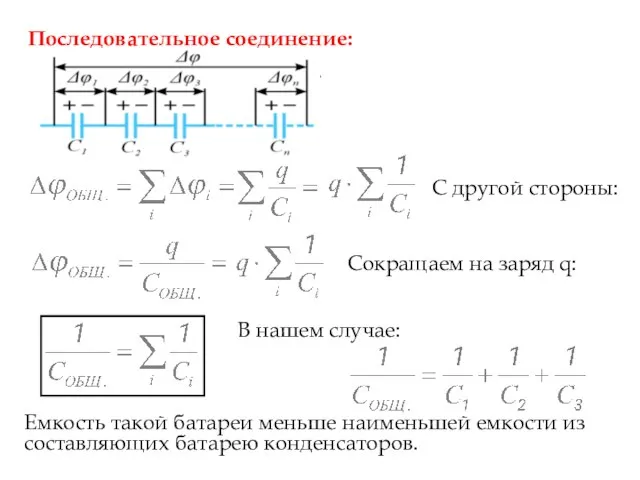
- 20. Последовательное соединение: С2 С3 С1 Δϕ1 Δϕ2 Δϕ3 С другой стороны: Сокращаем на заряд q: В
- 21. Энергия электрического поля Сообщение проводнику электрического заряда связано с совершением работы по преодолению кулоновских сил отталкивания
- 22. Для заряженного конденсатора : Учитывая, что конденсатор - это система из двух проводников, у которых q1=+q,
- 24. Скачать презентацию
















 Модель надёжности ветропарка с учётом погодных условий
Модель надёжности ветропарка с учётом погодных условий Презентация на тему Молекулы. Диффузия. Взаимодействие молекул
Презентация на тему Молекулы. Диффузия. Взаимодействие молекул  Абсолютно твердое тело. Сила. Задачи статики
Абсолютно твердое тело. Сила. Задачи статики Механические колебания
Механические колебания Простые механизмы. Момент силы. Золотое правило механики
Простые механизмы. Момент силы. Золотое правило механики Перенос графена на произвольную подложку
Перенос графена на произвольную подложку ДИНАМИКА в задачах (1)
ДИНАМИКА в задачах (1) Определение формул органических веществ. Необходимые теоретические сведения
Определение формул органических веществ. Необходимые теоретические сведения Электростатика
Электростатика Фотометрия Бугера, Ламберта, Бера
Фотометрия Бугера, Ламберта, Бера Измерение температуры
Измерение температуры Мощность. Единицы мощности
Мощность. Единицы мощности Температура.. Внутренняя энергия
Температура.. Внутренняя энергия ТО и ТР коробок передач
ТО и ТР коробок передач Магнитное поле. Сила Ампера
Магнитное поле. Сила Ампера Механика. Теория относительности А. Эйнштейна. Постулат постоянства скорости света
Механика. Теория относительности А. Эйнштейна. Постулат постоянства скорости света Трансформаторы
Трансформаторы طاقة الرياح
طاقة الرياح Работа газа и пара при расширении. Двигатели внутреннего сгорания
Работа газа и пара при расширении. Двигатели внутреннего сгорания Использование энергии Солнца на Земле
Использование энергии Солнца на Земле Вольтамперометрия. Вольтамперограмма
Вольтамперометрия. Вольтамперограмма Беседа Понятие об источниках тока
Беседа Понятие об источниках тока Расчёт пути и времени движения
Расчёт пути и времени движения Производная в физике и технике
Производная в физике и технике Машины и оборудование, инженерные системы и энергосберегающие технологии в городском хозяйстве и сфере услуг
Машины и оборудование, инженерные системы и энергосберегающие технологии в городском хозяйстве и сфере услуг Skaņa
Skaņa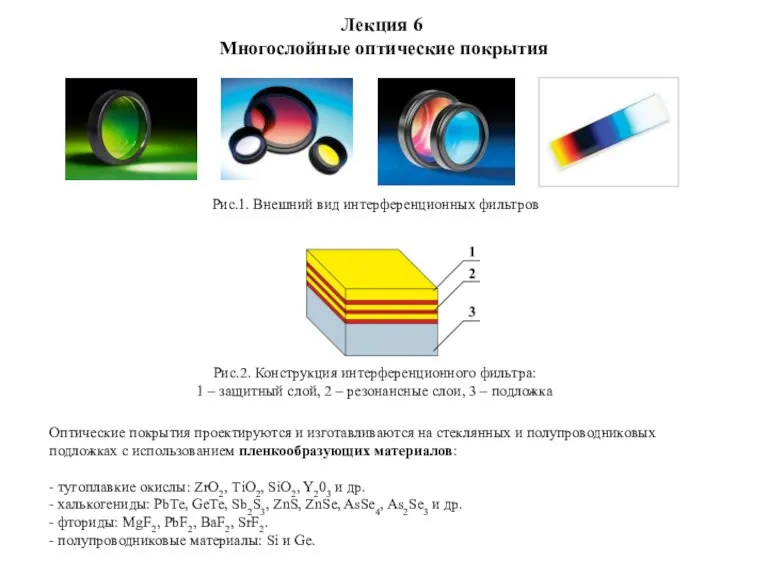 Многослойные оптические покрытия
Многослойные оптические покрытия Абсолютные и относительные величины
Абсолютные и относительные величины