Содержание
- 2. Л И Т Е Р А Т У Р А А. А. Детлаф, Б.М. Яворский Курс
- 4. М Е Х А Н И К А Классическая – v Релятивистская – v ~ c;
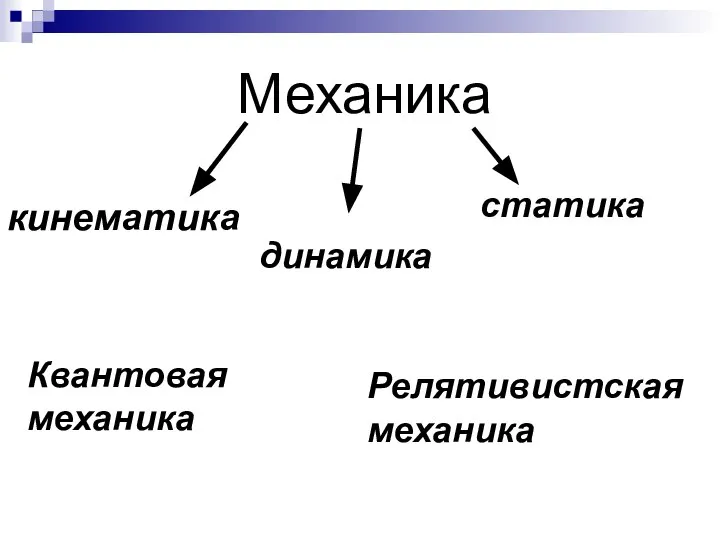
- 5. Механика кинематика динамика статика Квантовая механика Релятивистская механика Механика
- 6. Глава 1. Кинематика §1 Определения Совокупность тела отсчета, системы координат и синхронизованных между собой часов образуют
- 7. Основные понятия: система отсчета ( С О ), система координат ( СК ), материальная точка (
- 8. Физические модели Абсолютно твердым телом называется такое тело, расстояние между любыми двумя точками которого не изменяется
- 9. Различают движения Прямолинейное, криволинейное – по типу траектории. Равномерное , неравномерное – по виду кинематических уравнений.
- 10. Вращательным движением твердого тела называется такое при котором любая точка этого тела двигалась бы по окружности
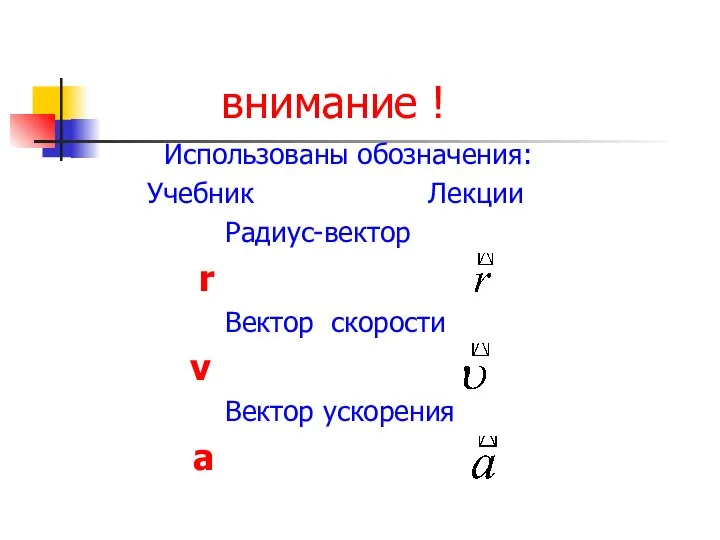
- 11. внимание ! Использованы обозначения: Учебник Лекции Радиус-вектор r Вектор скорости v Вектор ускорения а
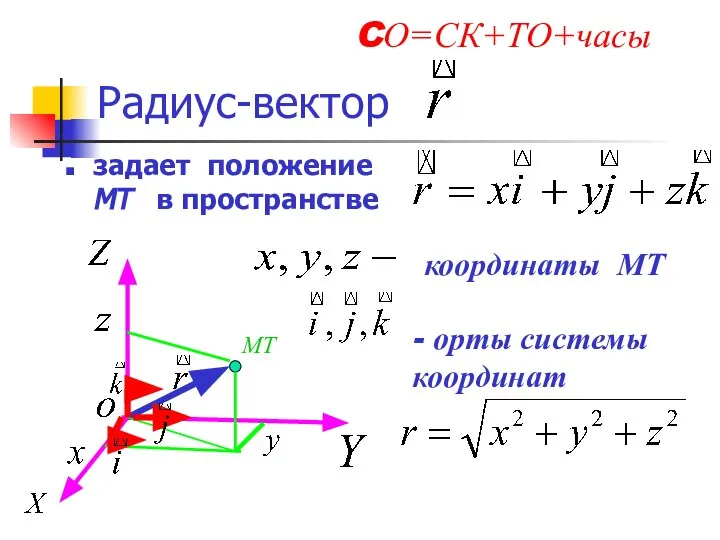
- 12. Радиус-вектор задает положение МТ в пространстве МТ - орты системы координат координаты МТ CО=СК+ТО+часы
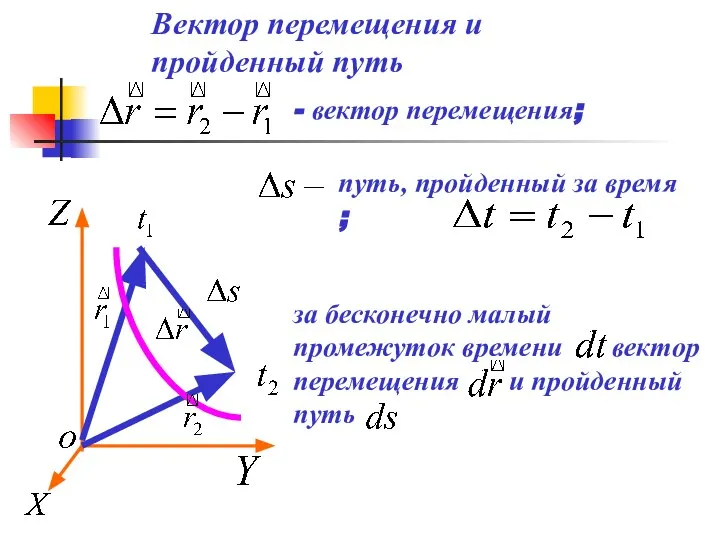
- 13. Вектор перемещения и пройденный путь - вектор перемещения; путь, пройденный за время ; за бесконечно малый
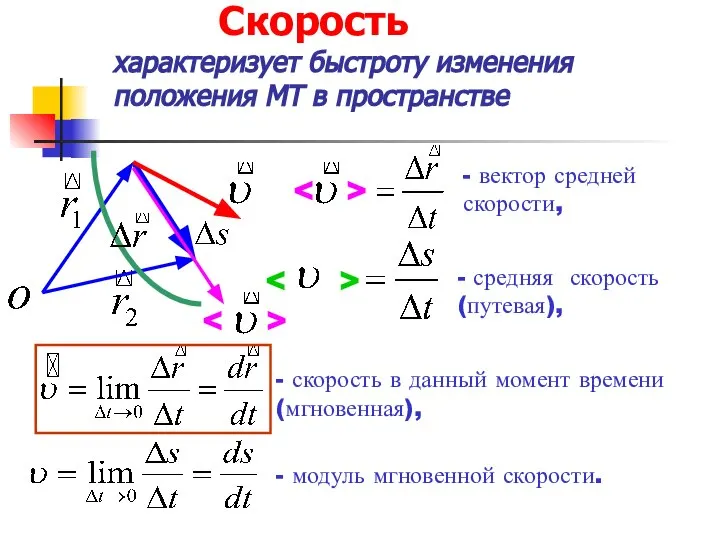
- 14. Cкорость характеризует быстроту изменения положения МТ в пространстве - скорость в данный момент времени (мгновенная), -
- 15. Скорость и ее проекции связаны соотношениями: (движение в плоскости ХОУ) y x - проекция вектора скорости
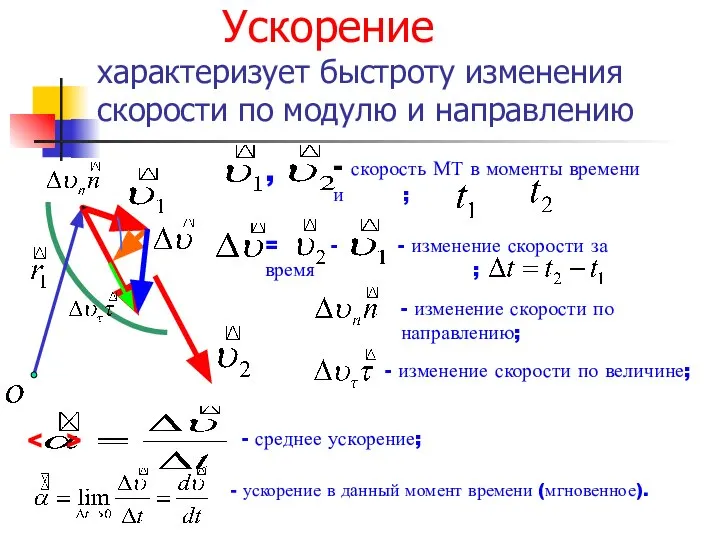
- 16. Ускорение характеризует быстроту изменения скорости по модулю и направлению , - скорость МТ в моменты времени
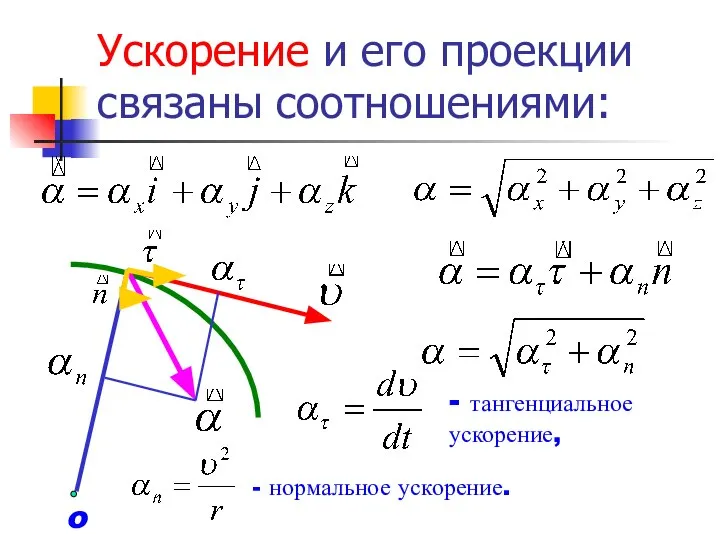
- 17. Ускорение и его проекции связаны соотношениями: - тангенциальное ускорение, - нормальное ускорение. o
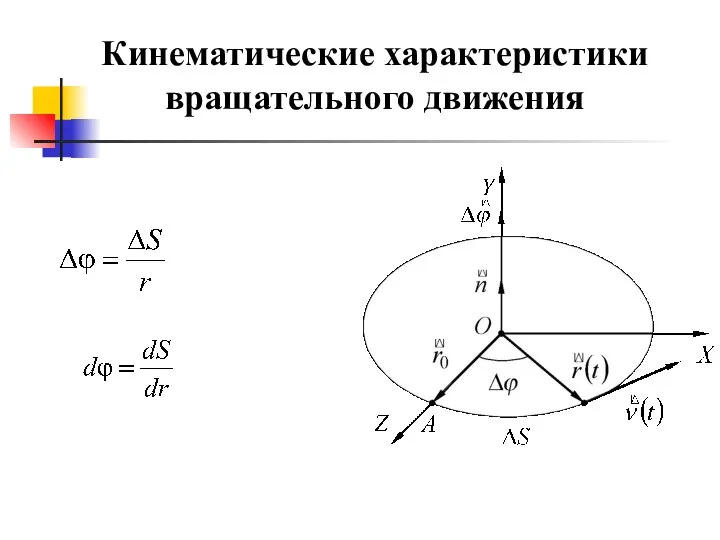
- 18. Кинематические характеристики вращательного движения
- 19. Вектор угловой скорости характеризует быстроту вращения точки и тела 3. Угловая скорость Мгновенная угловая скорость равна
- 20. 4. Угловое ускорение Мгновенное угловое ускорение равно первой производной от угловой скорости или второй производной от
- 21. Связь между линейными и угловыми характеристиками
- 22. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ДВИЖЕНИЯ Выражают зависимость от времени радиуса-вектора или координат :
- 23. Материальная точка: 1) тело, очень малых размеров; 2) тело, массой которого можно пренебречь в условиях данной
- 24. Вектор перемещения МТ: 1) вектор, соединяющий начальную и конечную точки траектории; 2) вектор, соединяющий начало координат
- 25. Модуль вектора перемещения и пройденный путь совпадают: 1) при свободном падении; 2) при криволинейном движении; 3)
- 26. Средняя скорость перемещения определяется по формуле: v = s / t; 2) = ∆ r /
- 27. Движение называют равномерным и прямолинейным, если 1) v = const; 2) v = const; 3) a
- 29. Скачать презентацию


















 Двигатель Стирлинга
Двигатель Стирлинга Методы исследования в биомеханике
Методы исследования в биомеханике Духовно-нравственное воспитание на уроках физики
Духовно-нравственное воспитание на уроках физики Биосенсоры
Биосенсоры Использование теплового действия электрического тока в устройстве теплиц и инкубаторов
Использование теплового действия электрического тока в устройстве теплиц и инкубаторов Презентация по физике _Ускорение. 9 класс_
Презентация по физике _Ускорение. 9 класс_ Состав и характеристика атомного ядра
Состав и характеристика атомного ядра Закон сохранения механической энергии
Закон сохранения механической энергии Электромагнитные волны
Электромагнитные волны Дефектация деталей
Дефектация деталей Основы теории цифровой модуляции и детектирования
Основы теории цифровой модуляции и детектирования Презентация на тему Механическое движение (7 класс)
Презентация на тему Механическое движение (7 класс)  Статические характеристики элементов автоматики
Статические характеристики элементов автоматики Давление жидкости и газа. Закон Паскаля
Давление жидкости и газа. Закон Паскаля Физика древесины
Физика древесины Майкл Фарадей (1791-1867)
Майкл Фарадей (1791-1867)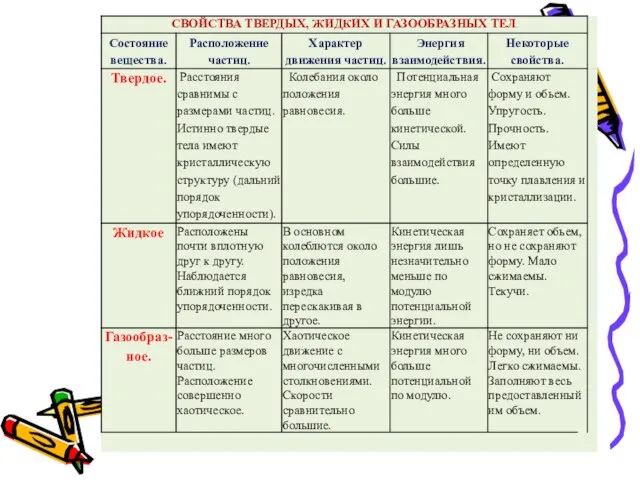 Свойства твердых, жидких и газообразных тел. Таблица
Свойства твердых, жидких и газообразных тел. Таблица Электрические явления
Электрические явления Явление тяготения. Сила тяжести
Явление тяготения. Сила тяжести Характеристики электрического поля. Конденсаторы
Характеристики электрического поля. Конденсаторы САD/CAE/CAM проектирование детали коленчатый вал
САD/CAE/CAM проектирование детали коленчатый вал Опорно-поворотное устройство и поворотный механизм
Опорно-поворотное устройство и поворотный механизм Сила трения
Сила трения Развитие теоретических принципов лазерной техники. Вклад А.М. Прохорова и Н.Г. Басова
Развитие теоретических принципов лазерной техники. Вклад А.М. Прохорова и Н.Г. Басова Частотные методы синтеза
Частотные методы синтеза Шаблон презентации по микро- и нанодиагностике
Шаблон презентации по микро- и нанодиагностике Tema_4_Para_sil_i_moment_sil_otnositelno_tochki_Ploskaya_sistema_proizvolno_raspolozhennykh_sil
Tema_4_Para_sil_i_moment_sil_otnositelno_tochki_Ploskaya_sistema_proizvolno_raspolozhennykh_sil Ошибки при синхронииации. Beamforming. Перераспределение частот
Ошибки при синхронииации. Beamforming. Перераспределение частот