Кинематика. Операции с векторами

Физика изучает наиболее общие законы формирования
и развития окружающей нас материи в ее наиболее примитивных формах,
которые принято называть неживой природой.
Поэтому можно утверждать, что физика является фундаментом всех естественных наук.

“Пусть будет стыдно тому, кто бездумно пользуется чудесами науки и техники, смысля в них не более того, что смыслит в ботанике корова, с удовольствием щиплющая траву.”
(А. Эйнштейн, 1903 г.)

МАТЕМАТИЧЕСКОЕ ВВЕДЕНИЕ
Операции с векторами

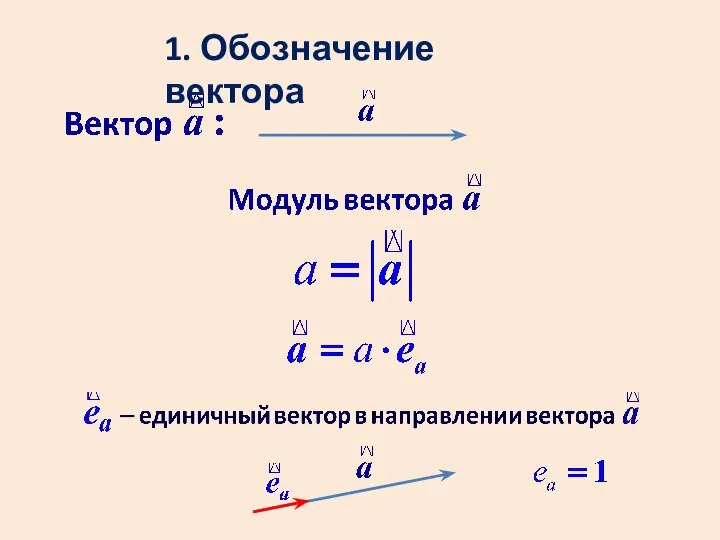
1. Обозначение вектора

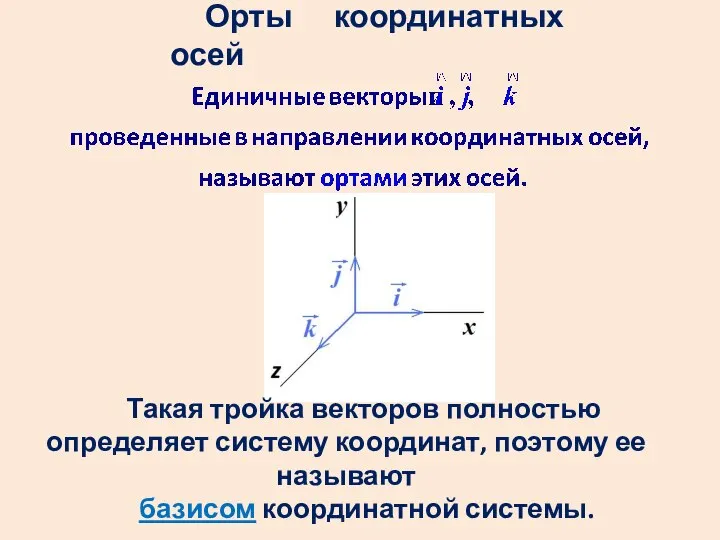
Орты координатных осей
Такая тройка векторов полностью определяет систему координат, поэтому ее называют базисом координатной системы.

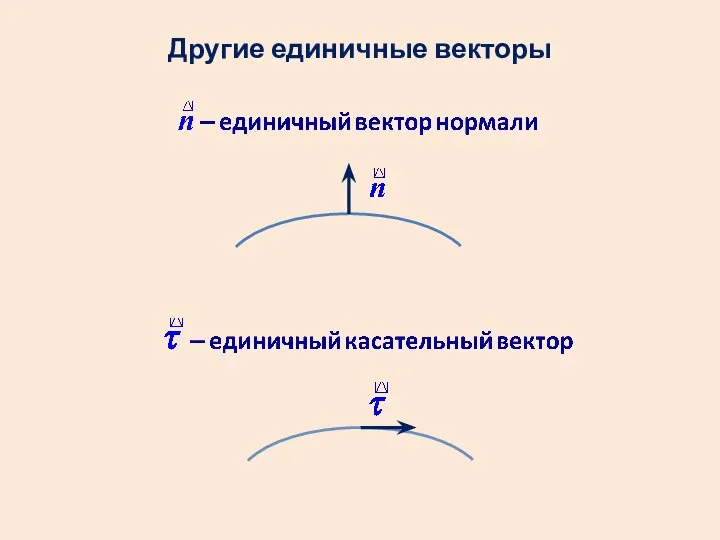
Другие единичные векторы

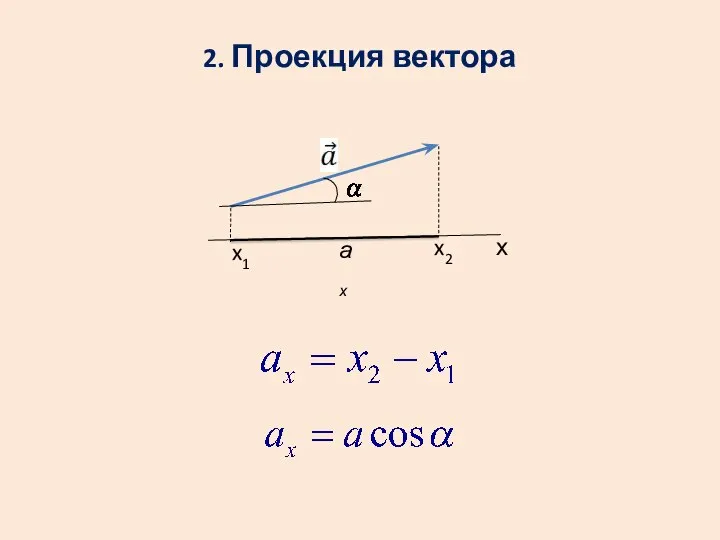
2. Проекция вектора
х
ах
x2
x1

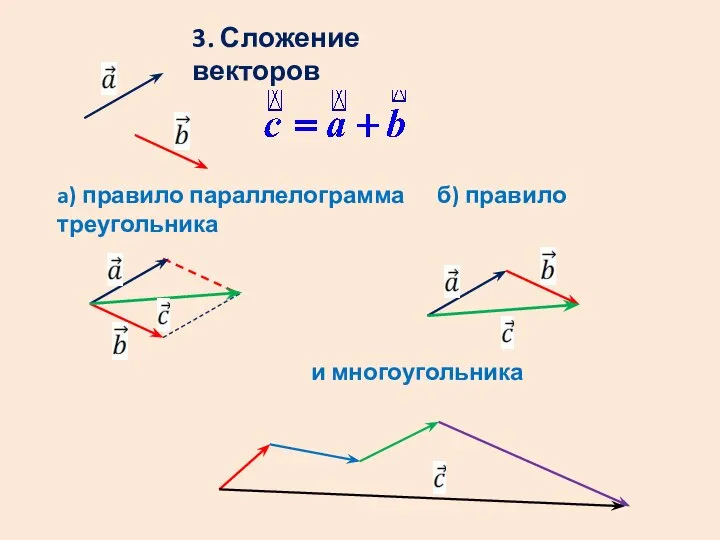
3. Сложение векторов
a) правило параллелограмма б) правило треугольника
и многоугольника

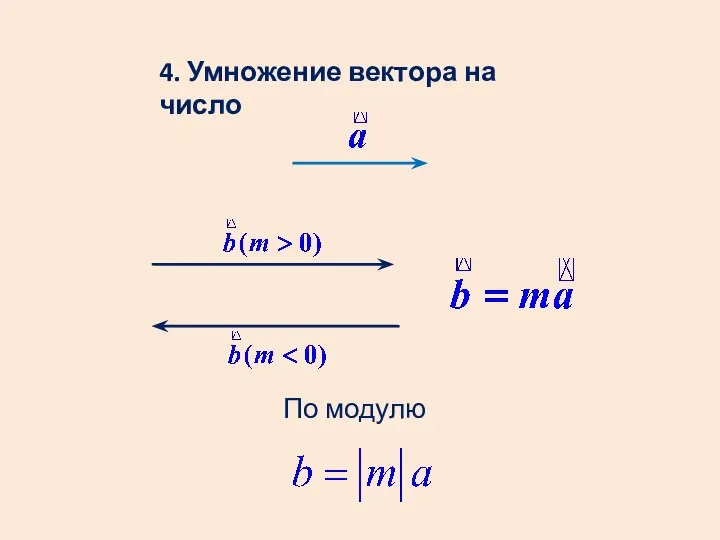
4. Умножение вектора на число
По модулю

5. Разложение вектора через проекции
х
y
z

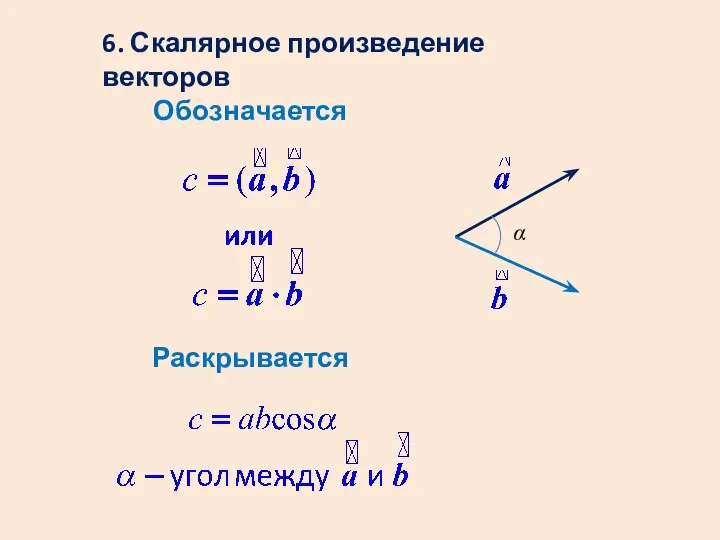
6. Скалярное произведение векторов
Обозначается
Раскрывается
α

Примеры

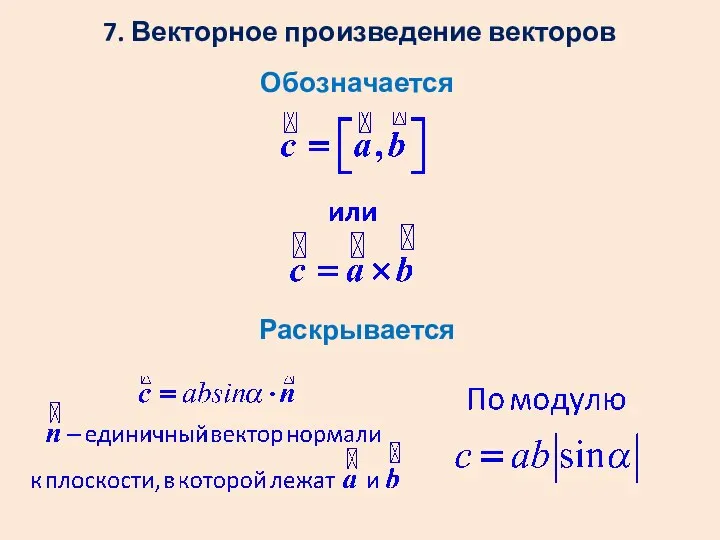
7. Векторное произведение векторов
Обозначается
Раскрывается

Вектор направлен по нормали к плоскости, в которой лежат векторы . Он перпендикулярен обоим векторам-сомножителям.

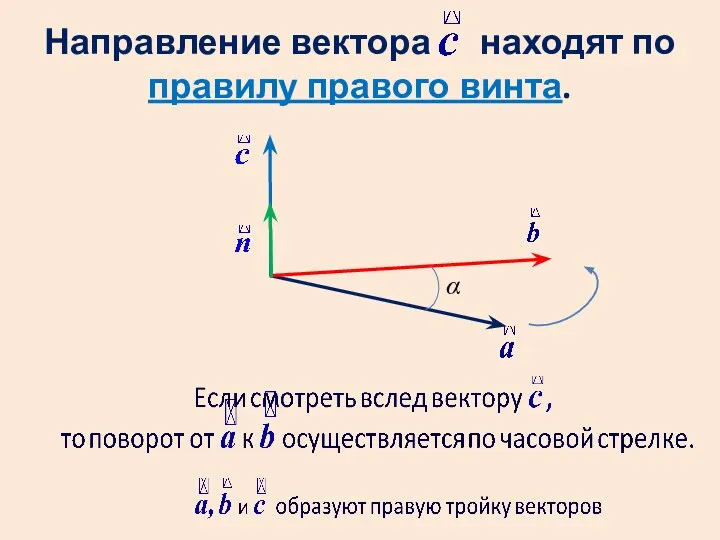
Направление вектора находят по правилу правого винта.
α

Примеры

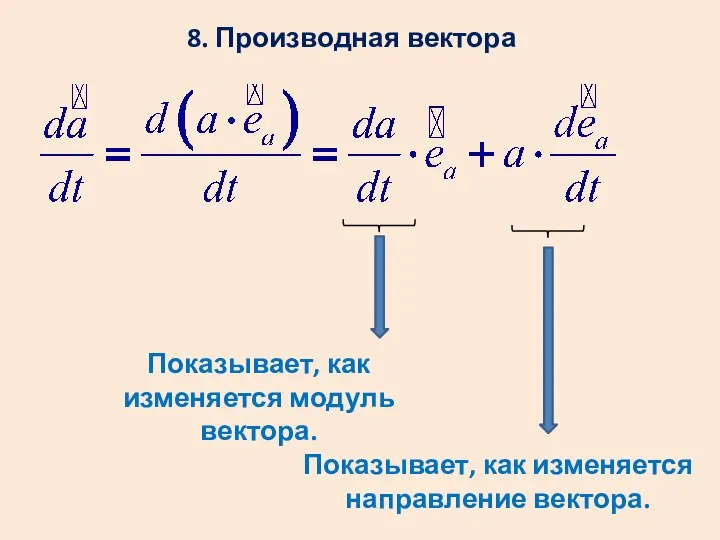
8. Производная вектора
Показывает, как изменяется модуль вектора.
Показывает, как изменяется направление вектора.

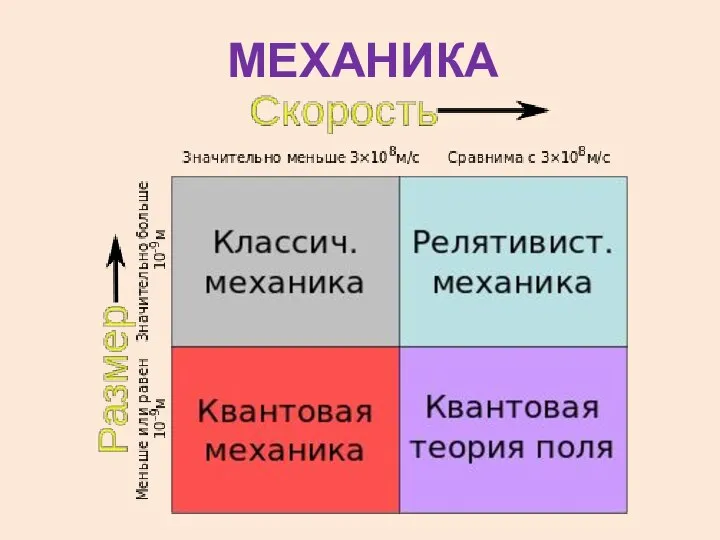
МЕХАНИКА

Механика изучает движение тел.
Механическое движение – изменение положения тела относительно других тел.
Для описания движения необходима система отсчёта: тело отсчёта, система координат, часы.

За тело отсчета принимают такое тело, которое в данной задаче можно условно считать неподвижным.
Тело отсчета

Основная задача механики-
– зная положение и скорость тела в начальный момент времени, определить положение и скорость тела в произвольный момент времени.

Реальные физические явления очень сложны и, как правило, возможно лишь приближенное их описание.
Для этого пользуются упрощающими моделями.

Материальная точка –
– тело, размерами и формой которого в данной задаче можно пренебречь.
(Массой – нельзя!)
Абсолютно твердое тело –
– такое тело, деформацией которого можно пренебречь.

ВИДЫ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Поступательное движение – все точки тела движутся одинаково. Любая прямая, связанная с телом, параллельна самой себе.
Достаточно описать движение одной точки.
Вращательное движение – точки тела движутся по окружностям, центры которых лежат на неподвижной прямой, называемой осью вращения.

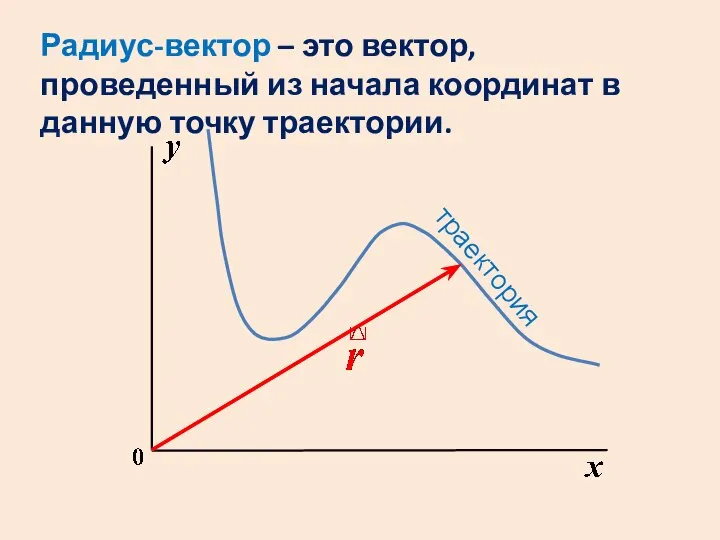
Траектория – линия, по которой движется материальная точка.
Положение точки на траектории можно задать либо с помощью координат х, y, z, либо с помощью радиус–вектора .
Кинематика материальной точки

траектория
Радиус-вектор – это вектор, проведенный из начала координат в данную точку траектории.

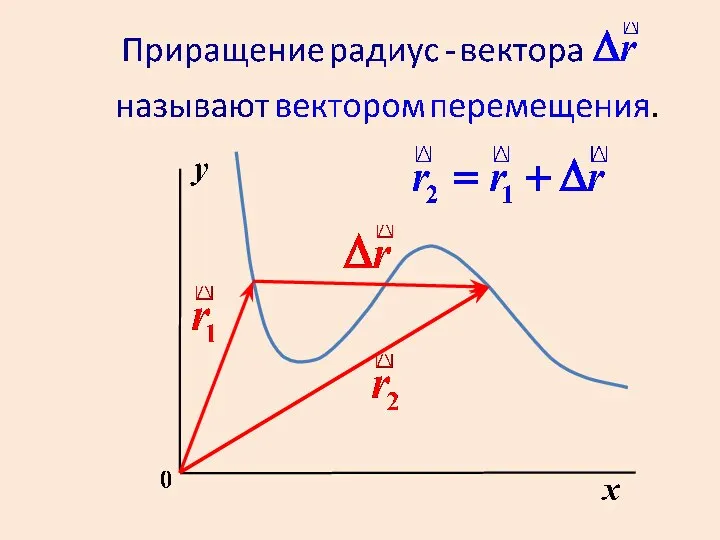
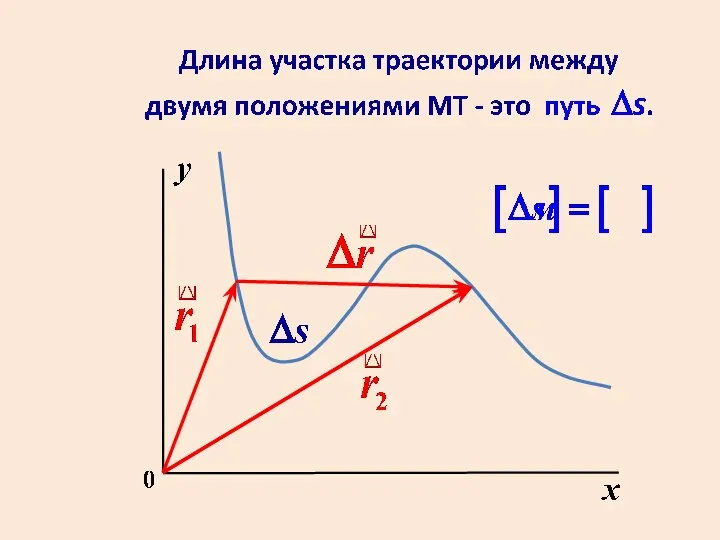
Путь и модуль вектора перемещения равны только в случае однонаправленного прямолинейного движения. Во всех других случаях путь больше.
Обе величины равны также при бесконечно малом перемещении.

СКОРОСТЬ
Скорость – это величина, характеризующая быстроту изменения радиус-вектора материальной точки со временем.

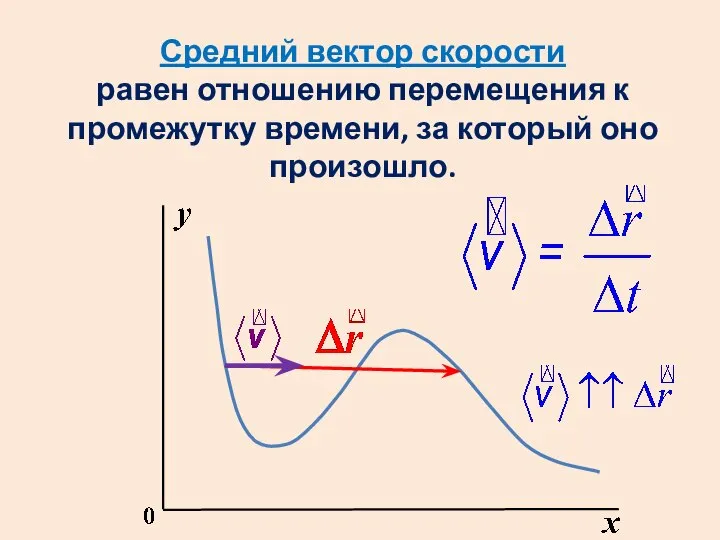
Средний вектор скорости
равен отношению перемещения к промежутку времени, за который оно произошло.

Средняя путевая скорость
(средний модуль скорости) равна отношению пути к промежутку времени, за который этот путь пройден.

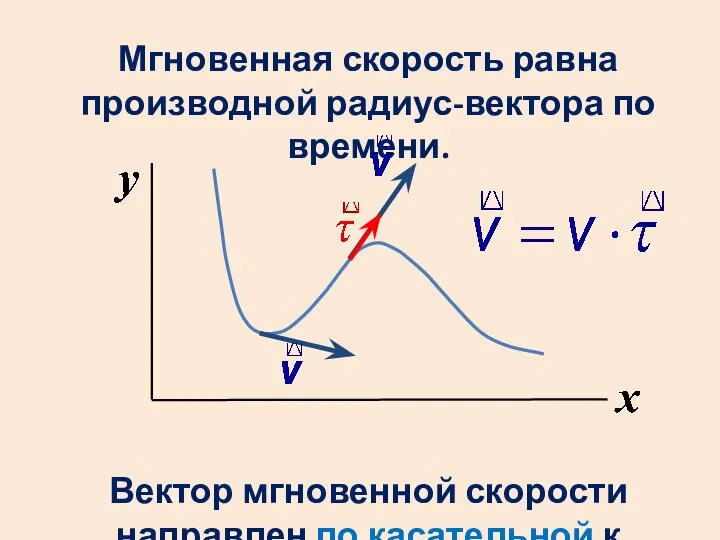
Мгновенная скорость – это скорость в данный момент времени. Ее находят как предел средней скорости при Δt→0.

Мгновенная скорость равна производной радиус-вектора по времени.
Вектор мгновенной скорости направлен по касательной к траектории.

Модуль мгновенной скорости
находят как производную пути по времени.

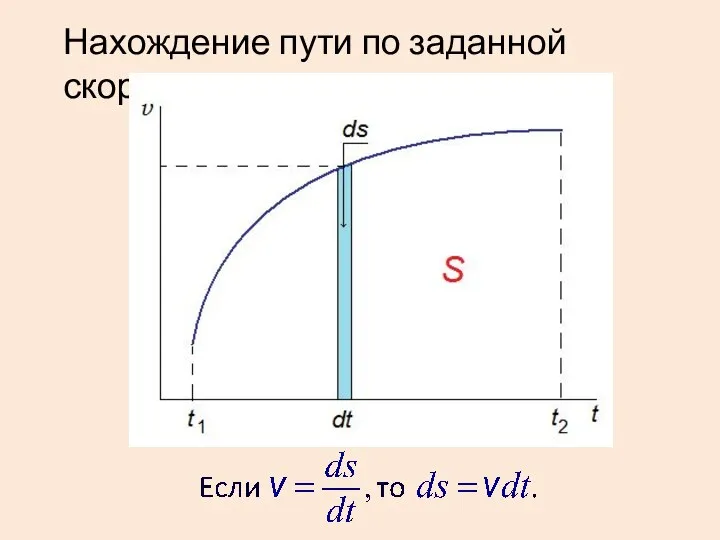
Нахождение пути по заданной скорости