Содержание
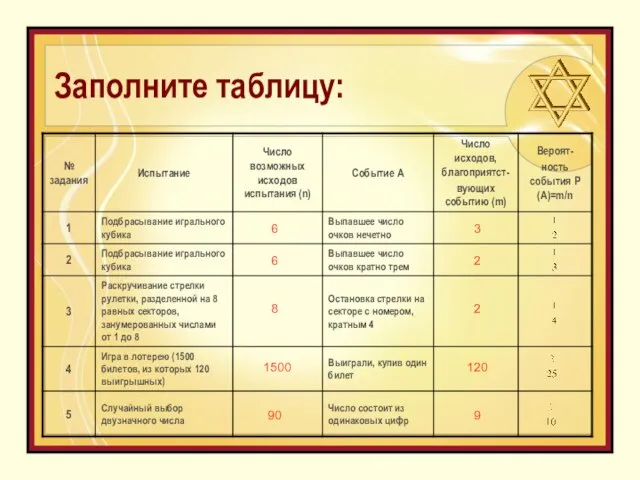
- 2. Заполните таблицу: 6 6 8 1500 90 3 2 2 120 9
- 3. Практикум по решению задач. Таня забыла последнюю цифру номера телефона знакомой девочки и набрала ее наугад.
- 4. Практикум по решению задач. На четырех карточках написаны буквы О, Т, К, Р. Карточки перевернули и
- 5. На четырех карточках написаны цифры 1, 2, 3, 4. Карточки перевернули и перемешали. Затем открыли наугад
- 6. На четырех карточках написаны цифры 1, 2, 3, 4. Карточки перевернули и перемешали. Затем открыли наугад
- 7. б) Событие В={ из трех карточек образовано число 312 и 321}, На четырех карточках написаны цифры
- 8. в)Событие С={из трех карточек образовано число, первая цифра которого 2}. Если первая цифра фиксирована, то на
- 9. Практикум по решению задач. В ящике лежат 1 белый и три черных шара. Наугад вынимаются 2
- 10. Практикум по решению задач. Cлучайным образом одновременно выбираются две буквы из 33 букв русского алфавита. Найдите
- 11. Практикум по решению задач. Cлучайным образом одновременно выбираются две буквы из 33 букв русского алфавита. Найдите
- 12. Практикум по решению задач. Cлучайным образом одновременно выбираются две буквы из 33 букв русского алфавита. Найдите
- 13. Практикум по решению задач. Cлучайным образом одновременно выбираются две буквы из 33 букв русского алфавита. Найдите
- 15. Скачать презентацию











 Теория пластин
Теория пластин Работа и мощность электрического тока
Работа и мощность электрического тока Скорость движения
Скорость движения Узгоджувальні пристрої. Лекція 2
Узгоджувальні пристрої. Лекція 2 Второе начало термодинамики. Принцип действия тепловой машины и ее КПД. Лекция 6
Второе начало термодинамики. Принцип действия тепловой машины и ее КПД. Лекция 6 Электрический ток
Электрический ток Энергетические установки в космосе
Энергетические установки в космосе Квантовая радиофизика
Квантовая радиофизика Презентация на тему Внутренняя энергия. Количество теплоты
Презентация на тему Внутренняя энергия. Количество теплоты  Система пуска двигателя
Система пуска двигателя Силы. Действие силы
Силы. Действие силы Презентация на тему Приливы, отливы, их использование 9 класс
Презентация на тему Приливы, отливы, их использование 9 класс  Допуски и посадки
Допуски и посадки Освещение. Свет и тень
Освещение. Свет и тень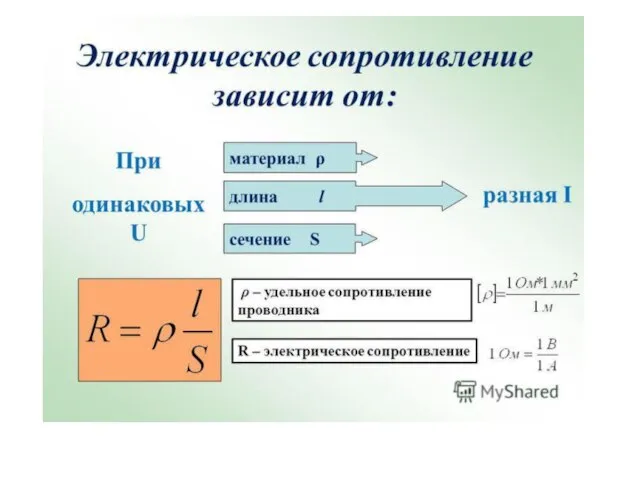 Электрическое сопротивление
Электрическое сопротивление Применение первого начала термодинамики к изопроцессам
Применение первого начала термодинамики к изопроцессам Дви́гатель вну́треннего сгора́ния (ДВС)
Дви́гатель вну́треннего сгора́ния (ДВС) Энергия топлива. Удельная теплота сгорания
Энергия топлива. Удельная теплота сгорания Цифровые измерительные приборы. Мультиметр
Цифровые измерительные приборы. Мультиметр Цепи переменного тока с последовательным соединением элементов
Цепи переменного тока с последовательным соединением элементов Основные Законы Природы
Основные Законы Природы Живой свет свечи
Живой свет свечи Преломление света. Физический смысл показателя преломления. Электромагнитные явления
Преломление света. Физический смысл показателя преломления. Электромагнитные явления Лед и соль!
Лед и соль! Дробилка безрешетная
Дробилка безрешетная Презентация на тему Перемещение при прямолинейном равноускоренном движении (9 класс)
Презентация на тему Перемещение при прямолинейном равноускоренном движении (9 класс)  Уравнение движения
Уравнение движения Изобретения, подсказанные природой
Изобретения, подсказанные природой