Содержание
- 2. Энергия гармонического осциллятора Свободные колебания любого осциллятора в отсутствие трения будут гармоническими, если действующая в нем
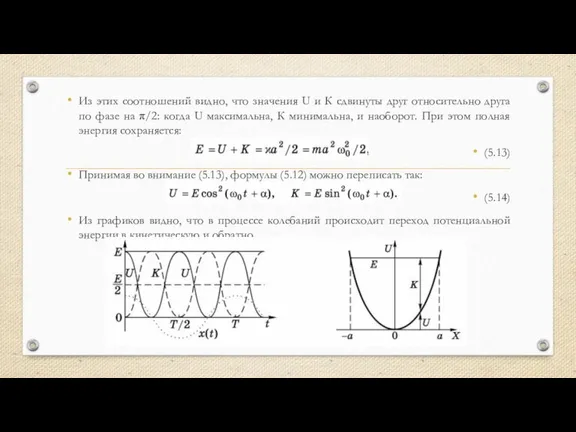
- 3. Из этих соотношений видно, что значения U и К сдвинуты друг относительно друга по фазе на
- 4. Сложение колебаний одного направления Можно изобразить колебания графически с помощью вектора-амплитуды а, вращающегося с угловой скоростью
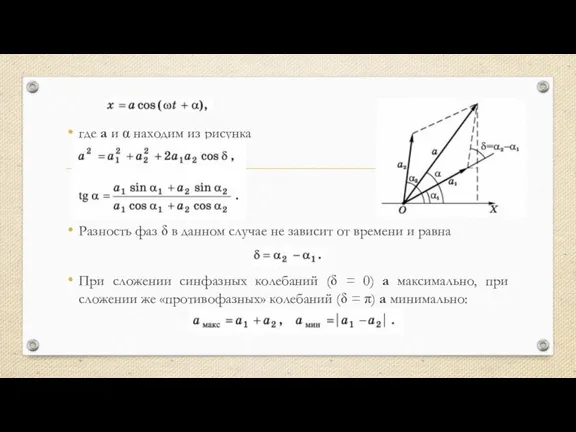
- 5. где а и α находим из рисунка Разность фаз δ в данном случае не зависит от
- 6. 2) Случай, когда | ω1 = ω2 | Амплитуда колебаний описывается той же формулой, что в
- 7. Сложение взаимно перпендикулярных колебаний Рассмотрим случай, когда частоты складываемых колебаний одинаковы. Пусть координаты х и у
- 8. Фигуры Лиссажу Если частоты взаимно перпендикулярных колебаний не одинаковы и относятся как целые числа, то траектории
- 9. Уравнение затухающих колебаний
- 11. Характеристики затухания
- 12. Уравнение вынужденных колебаний Чтобы возбудить в системе незатухающие колебания, необходимо компенсировать потери энергии, обусловленные силами сопротивления
- 14. Скачать презентацию









 Дисперсия света
Дисперсия света Пневматика
Пневматика Механика. Основы СТО
Механика. Основы СТО Интерпретация спектральной классификации. (Тема 18)
Интерпретация спектральной классификации. (Тема 18) Изменение импульса механической системы
Изменение импульса механической системы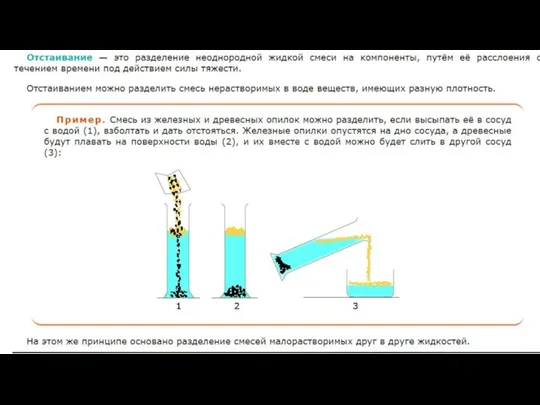 Разделение смесей
Разделение смесей Внутренняя энергия
Внутренняя энергия Магнитные материалы. Гистерезис. Применение ферромагнитных материалов
Магнитные материалы. Гистерезис. Применение ферромагнитных материалов Фотографии для иллюстрации закономерностей оптики
Фотографии для иллюстрации закономерностей оптики Презентация на тему Диффузия в газах жидкостях и твердых телах (7 класс)
Презентация на тему Диффузия в газах жидкостях и твердых телах (7 класс)  Определение эффекта Томпсона
Определение эффекта Томпсона Отражение света
Отражение света Суд над атомом. Мультимедийный урок
Суд над атомом. Мультимедийный урок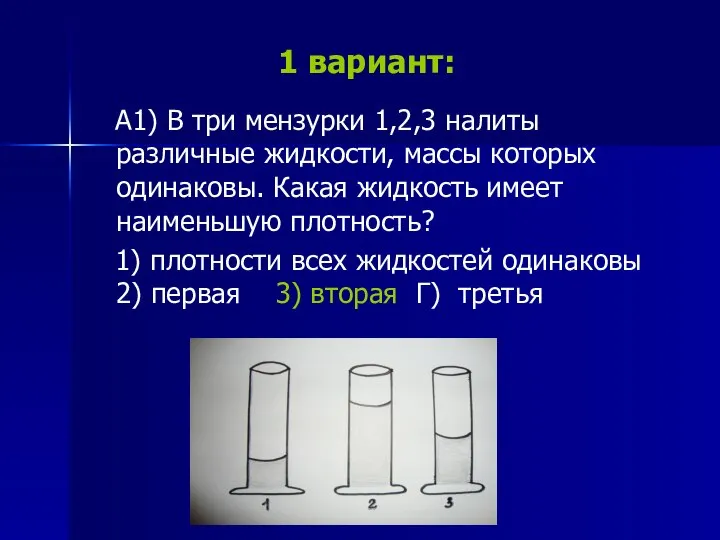 Задачи на плотность
Задачи на плотность Магнитное взаимодействие Изучение свойств магнита Учитель И.А. Попова
Магнитное взаимодействие Изучение свойств магнита Учитель И.А. Попова Сила трения. Трение в природе и технике. Явление трения
Сила трения. Трение в природе и технике. Явление трения Вибрация подшипников качения
Вибрация подшипников качения Занимательные опыты по физике
Занимательные опыты по физике Тест по теме Электрический ток
Тест по теме Электрический ток Строение жидкостей, аморфных тел и жидких кристаллов. Лекция 6
Строение жидкостей, аморфных тел и жидких кристаллов. Лекция 6 Методы измерения потерь в оптических волокнах
Методы измерения потерь в оптических волокнах Явление тяготения. Сила тяжести
Явление тяготения. Сила тяжести Простые механизмы: Рычаг
Простые механизмы: Рычаг Точность механической обработки и погрешности изготовления деталей
Точность механической обработки и погрешности изготовления деталей Давление жидкости и газа. Закон Паскаля
Давление жидкости и газа. Закон Паскаля Состояние вещества. Тест
Состояние вещества. Тест Ферромагнетики. Относительная магнитная проницаемость вещества
Ферромагнетики. Относительная магнитная проницаемость вещества Управляемость. Тема 6
Управляемость. Тема 6