Слайд 2200
ВОПРОСЫ
23. Гармонические колебания. Характеристики гармонических колебаний. Векторная диаграмма.
24. Сложение колебаний одного направления

и частоты. Биения. Сложение взаимно перпендикулярных колебаний.
25. Уравнение динамики незатухающих колебаний. Пружинный маятник.
Слайд 3200
23. Гармонические колебания. Характеристики гармонических колебаний. Графическое представление гармонических колебаний. Векторная диаграмма.

Фазовая плоскость.
Слайд 4200
Колебания – процессы отличающиеся той или иной степенью повторяемости.

Слайд 5200
Дифференциальное уравнение гармонических колебаний:
Закон кинематики гармонических колебаний – колебаний, которые совершаются по

закону синуса или косинуса (решение дифференциального уравнения):
Слайд 6200
x – смещение или колеблющаяся величина,
A – амплитуда колебаний – максимальное смещение

или максимальное значение колеблющейся величины,
(ω0t + α) – величина, стоящая под знаком косинуса или синуса – фаза колебаний,
Слайд 7200
ω0 – собственная частота, она же циклическая частота – количество колебаний

за 2π секунды,
α – начальная фаза (для момента времени t = 0),
T – период, время, за которое фаза получает приращение 2π или время одного колебания (цикла),
Слайд 8200
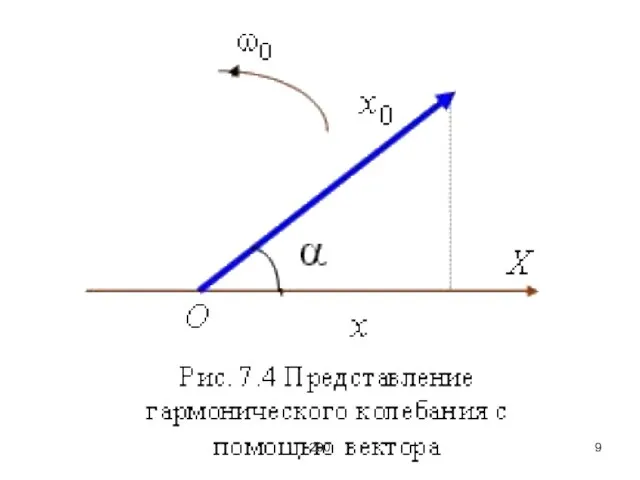
Векторная диаграмма
(векторное изображение колебаний)
Возьмём ось X. Из точки О отложим вектор a

под углом α к оси. Если привести этот вектор во вращение с угловой скоростью ω0, то проекция конца вектора будет перемещаться по оси X в пределах от –a до +a, по закону x = a cos(ω0t + α).
Слайд 10200
Фазовая плоскость
На фазовой плоскости для координат используют значения колеблющейся величины (ось абсцисс

– X) и её скорость (ось ординат – Y).
Слайд 11200
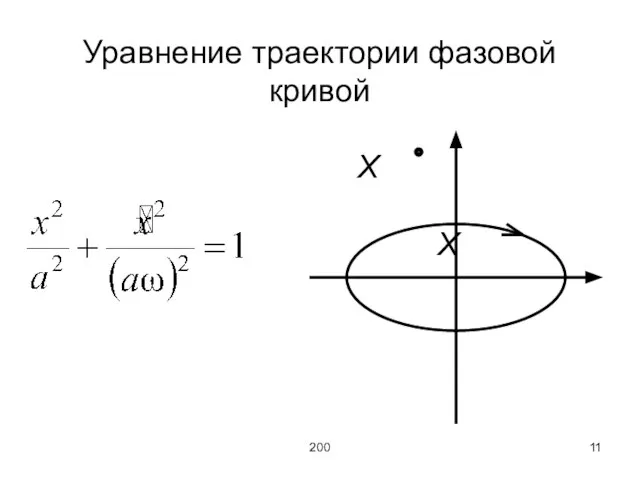
Уравнение траектории фазовой кривой
X
X
Слайд 13200
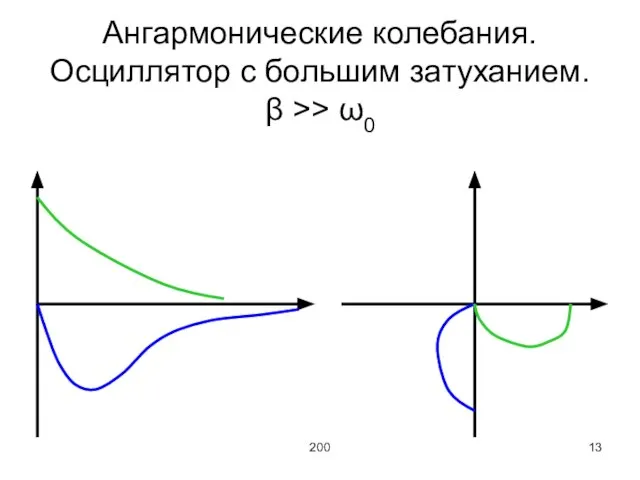
Ангармонические колебания.
Осциллятор с большим затуханием.
β >> ω0
Слайд 14200
Предельный случай β = ω0
Этот случай в технике важен тем, что при

таком соотношении параметров в случае внешнего воздействия система может вернуться в исходное состояние. (Из-за силы трения система может не вернуться в исходное положение)
Слайд 16200
24. Сложение колебаний одного направления и частоты. Биения. Сложение взаимно перпендикулярных колебаний.

Частные случаи.
Слайд 17200
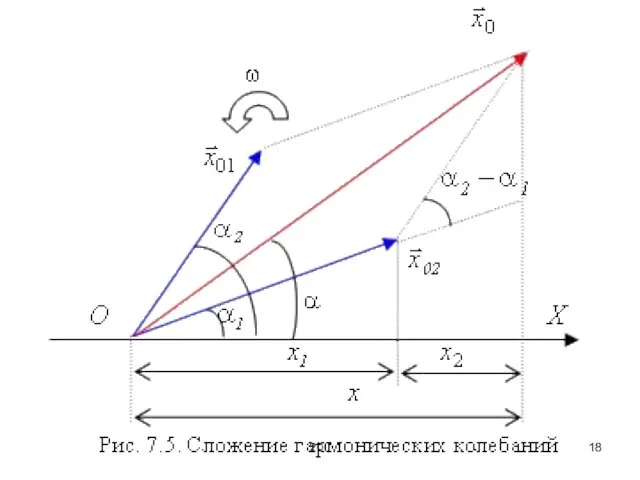
Рассмотрим сложение двух гармонических колебаний
x1 = a1 cos(ω0t + φ1), x2

= a2 cos(ω0t + φ2).
В соответствии с теоремой косинусов и рисунком запишем амплитуду результирующего колебания
a2 = a12 + a22 + 2a1a2cos(φ2 – φ1).
Слайд 19200
Фаза результирующего колебания вычисляется следующим образом

Слайд 20200
Если φ2 ≠ φ1 то говорим о векторном сложении векторов,
Если φ2

= φ1 то говорим о скалярном сложении векторов:
x = x1 + x2 = (a1 + a2) cos(ω0t + φ).
Слайд 22200
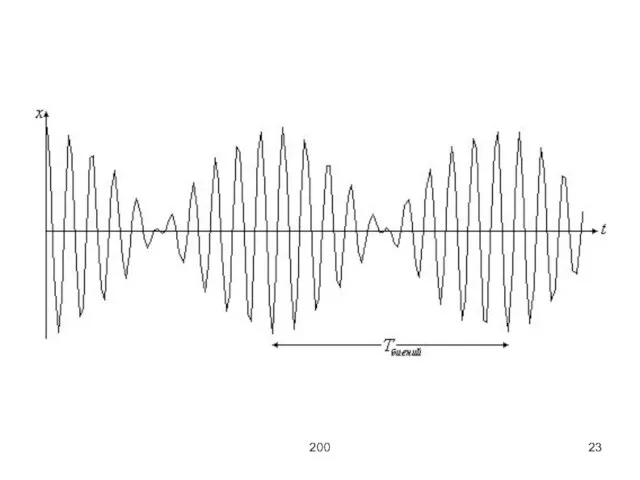
Биения – колебания с пульсирующей амплитудой, которые получаются в результате сложения двух

колебаний, обладающими незначительно отличающимися частотами.
Слайд 24200
Складываемые колебания
x1 = a cos(ωt), x2 = a cos((ω + Δω)t),
Результирующее

колебание
x=x1+x2=2acos(Δωt/2)cos((ω+Δω/2)t)≈ ≈ 2a cos(Δωt/2) cos(ωt).
Амплитуда результирующего колебания и период пульсаций
Слайд 25200
Сложение взаимно перпендикулярных колебаний
Запишем уравнения колебаний в следующей форме:
x = a

cos(ωt), y = b cos(ωt + α).
Это параметрическая форма записи.
Слайд 26200
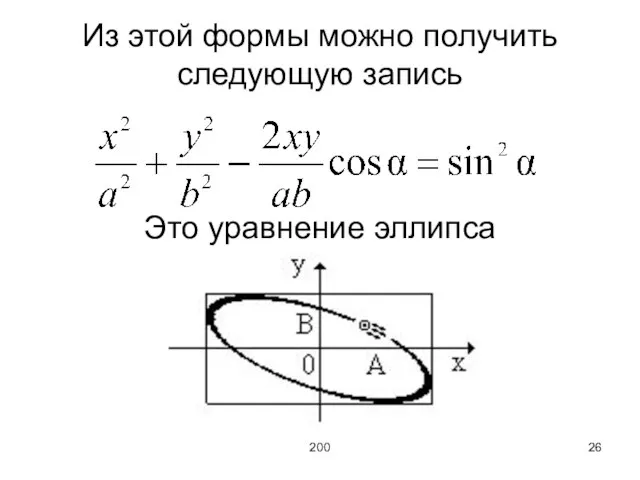
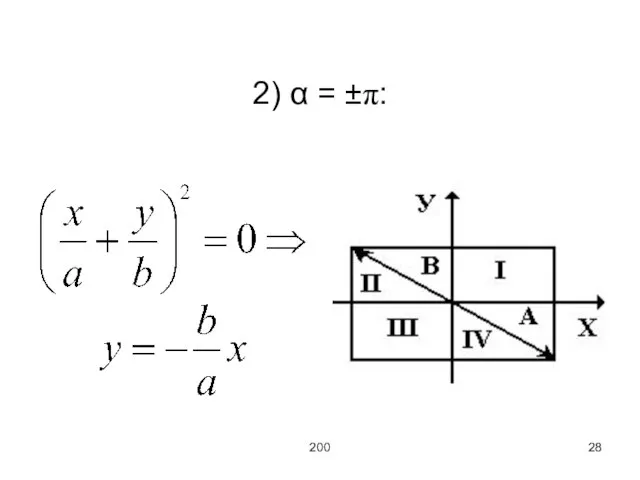
Из этой формы можно получить следующую запись
Это уравнение эллипса
Слайд 27200
В зависимости от фазы α получаем тот или иной вид колебаний. Рассмотрим
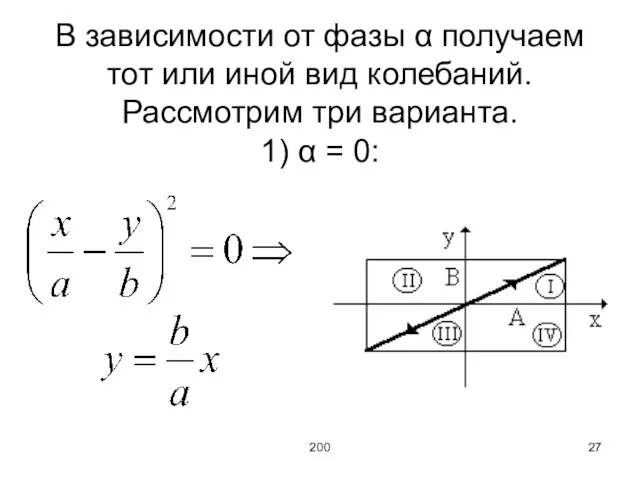
три варианта.
1) α = 0:
Слайд 29200
1) α = ±π/2:
Если a = b, то получаем окружность:
х2 +

у2 = R2.
Слайд 30200
Если α = + π/2, то точка на траектории будет двигаться по
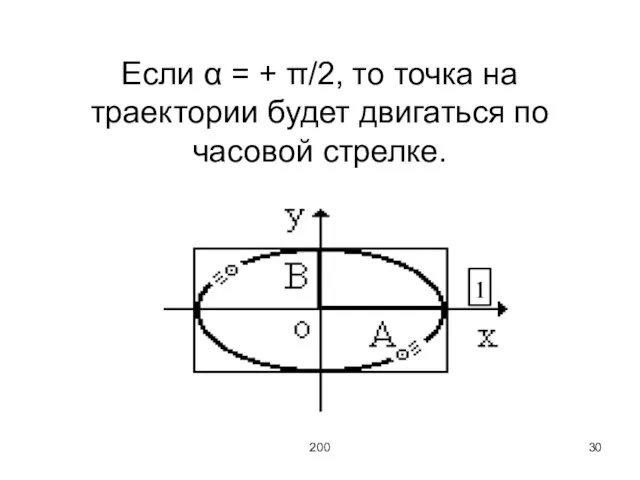
часовой стрелке.
Слайд 31200
Если α = − π/2, то точка на траектории будет двигаться против
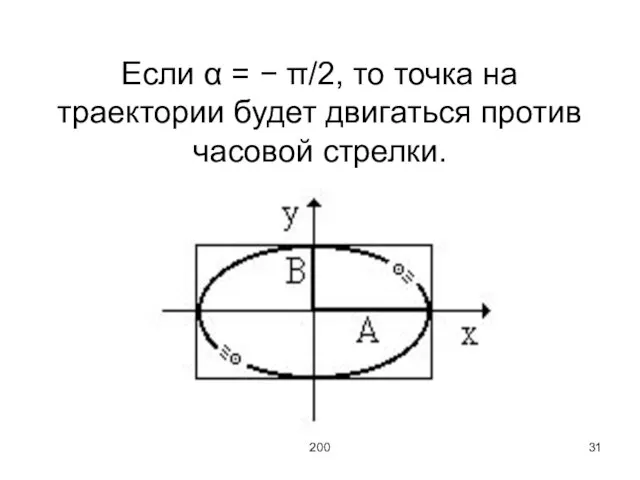
часовой стрелки.
Слайд 32200
При сложении взаимно перпендикулярных колебаний с различными амплитудами и частотами ωx ≠

ωy и неодинаковыми начальными фазами возникают сложные результирующие колебания, которые называют фигурами Лиссажу.
Слайд 33200
Если соотношение частот
и разность фаз складываемых колебаний α = π/2, наблюдается
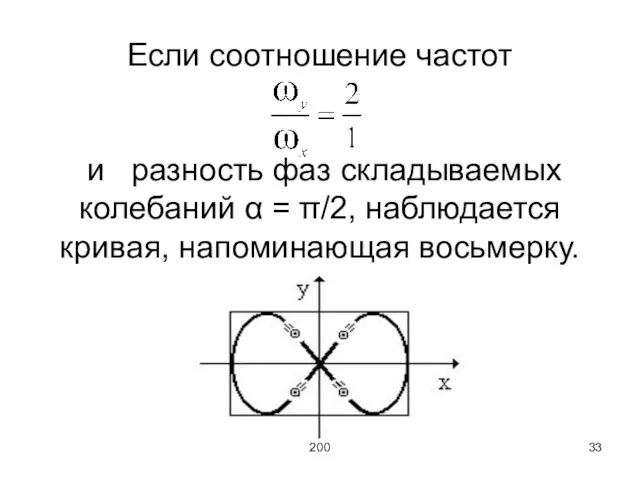
кривая, напоминающая восьмерку.
Слайд 34200
При отношении круговых частот
и разности фаз складываемых колебаний α = π/2

наблюдается более сложная кривая.
Слайд 35200
Замечание 1: Число касаний фигуры Лиссажу со сторонами прямоугольника, образованного амплитудами, равно

величине отношения частот.
Слайд 36200
Замечание 2: Если частоты складываемых колебаний кратны nω и mω, тогда уравнения

взаимно перпендикулярных колебаний запишутся в виде
Слайд 37200
Траектория результирующего колебания будет замкнутой, её форма зависит от амплитуд a и

b, круговых частот nω и mω и значений начальных фаз α1 и α2.
Слайд 38200
Комплексные числа
Представление колебаний в комплексной форме
Комплексное число
z = x + iy,
x, y

– вещественные числа,
i2 = – 1 – мнимая единица.
Слайд 40200
x = Re z – вещественная часть,
y = Im z – мнимая

часть,
z* = x – iy – комплексно сопряжённое числу z = x + iy,
– модуль,
φ = arctg(y/x) – аргумент.
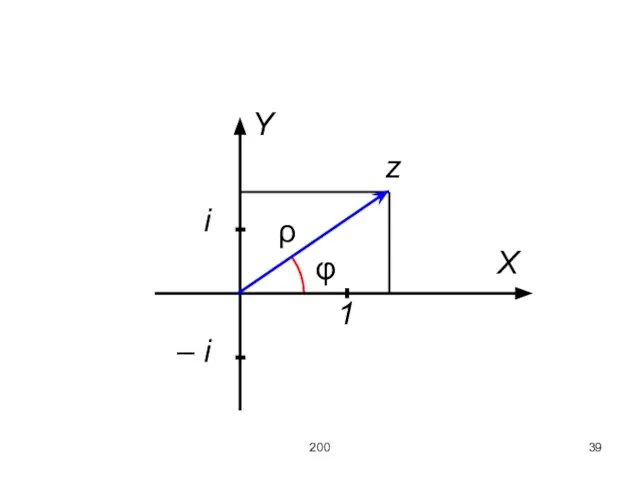
Слайд 41200
x = ρ cos φ,
y = ρ sin φ,
отсюда
z = ρ(cos φ

+ i sin φ),
Формула Эйлера:
– комплексная форма,
Слайд 44200
25. Уравнение динамики незатухающих колебаний. Пружинный, физический и математический маятники.

Слайд 45200
Рассмотрим систему, с одной степенью свободы. Потенциальная энергия системы будет функцией одной

переменной x: U = U(x). Система обладает положением устойчивого равновесия в точке
x = 0. В этом положении функция U(x) имеет минимум. Будем отсчитывать координату и потенциальную энергию от этого положения равновесия U(0) = 0.
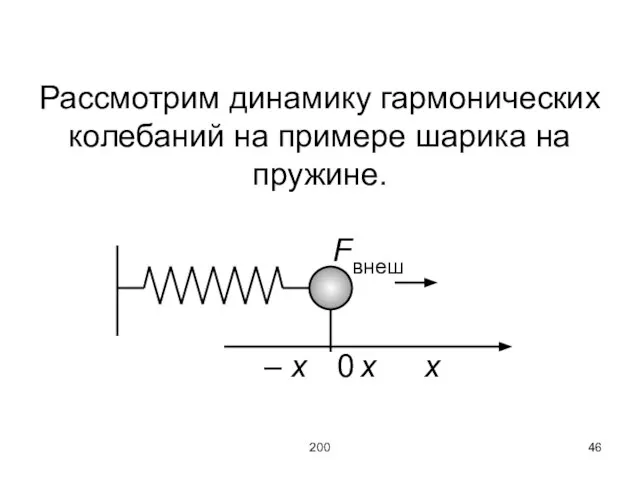
Слайд 46200
Рассмотрим динамику гармонических колебаний на примере шарика на пружине.
Fвнеш
– x 0 x x
Слайд 47200
Потенциальная энергия пружины
Сила действующая на пружину
Если сила по своей природе не является

упругой, но соответствует данному выражению, то её называют квазиупругой.
Слайд 48200
Запишем 2-й закон Ньютона для данной системы

Слайд 49200
Получим это же выражение из энергетических соотношений. Запишем полную механическую энергию системы

и продифференцируем:
Слайд 50200
В отсутствие сил трения движение под действием квазиупругой силы описывается дифференциальным уравнением
Такие

колебания называются свободными незатухающими.
Слайд 51200
Решение уравнения
имеет вид
Это закон гармонических колебаний – колебаний, которые совершаются по закону

синуса или косинуса.
Слайд 52200
Гармонический осциллятор –физическая система, поведение которой подчиняется уравнениям (динамическому и кинематическому):

Слайд 53200
Вообще, можно говорить о модели гармонического осциллятора. Рассмотри несколько примеров гармонических осцилляторов.

Слайд 54200
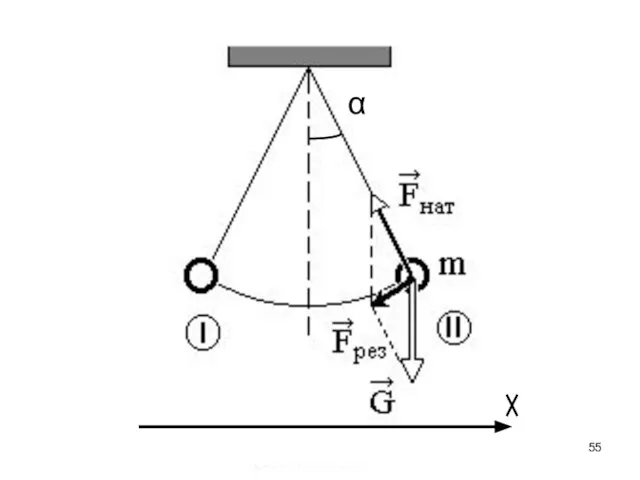
Математический маятник – материальная точка массы m на нерастяжимой нити длины ℓ.
Действующие

силы на точку
Слайд 56200
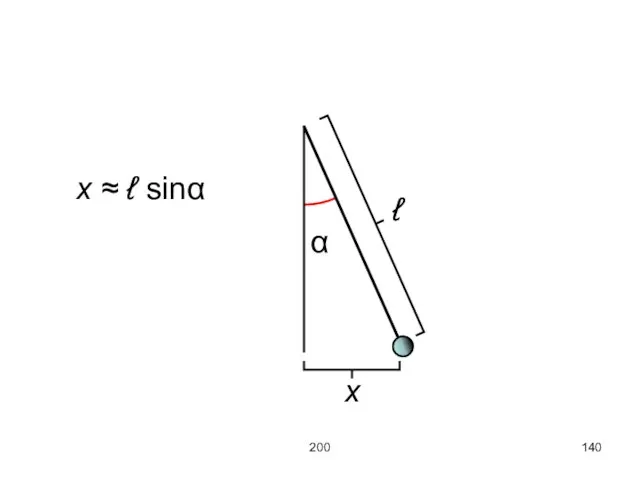
Запишем проекцию на касательную
воспользуемся следующими формулами (угол α очень мал)
x/ - расстояние,

пройденное точкой по дуге. В итоге получаем уравнение
Слайд 57200
Можно переписать это уравнение не для угла отклонения α, а для смещения

x вдоль оси X. Используем формулы
В итоге получаем уравнение
Слайд 58200
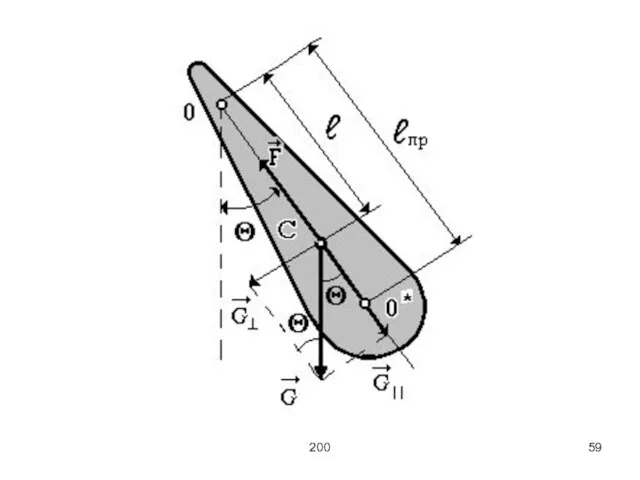
Физический маятник – реальная колебательная система. Физический маятник – некоторое тело, совершающее

колебания относительно оси, непроходящей через центр масс.
Запишем 2-й закон Ньютона для вращательного движения
Слайд 60200
В случае малых колебаний получаем закон гармонического осциллятора
здесь m – масса тела,

ℓ – расстояние от точки подвеса до центра масс, J – момент инерции относительно точки подвеса (оси качания), M – момент сил, действующий на тело.
Слайд 61200
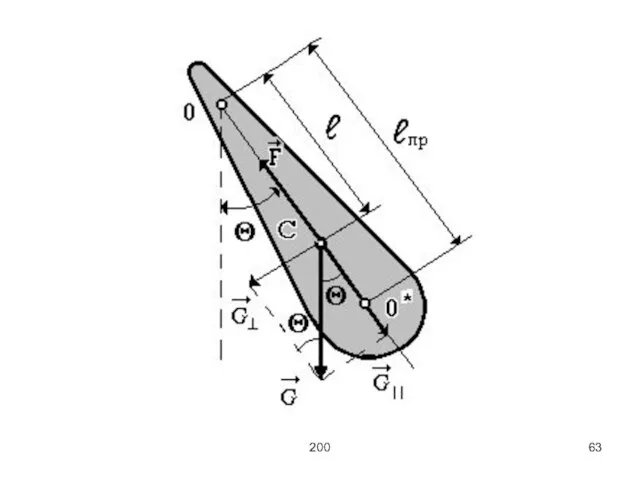
Приведенной длиной физического маятника называют длину такого математического маятника, когда периоды их

колебаний совпадают
(Тфиз = Тматем):
Слайд 62200
Приведенная длина физического маятника
расстояние между точками 0 и 0* и есть

приведенная длина
физического маятника. Сами точки 0 и 0* взаимозаменяемы, т. е. при замене точки 0 на 0* и обратно период колебаний физического маятника сохраняется неизменным.
Слайд 64200
Согласно теореме Штейнера момент инерции можно представить следующим способом:
I0 – момент инерции

тела относительно оси, проходящей через центр масс.
Если ℓ = ℓ0 (ℓ0 – радиус инерции), то период колебаний такого маятника будет минимальным.
Слайд 65200
Колебательный контур (электрические колебания)
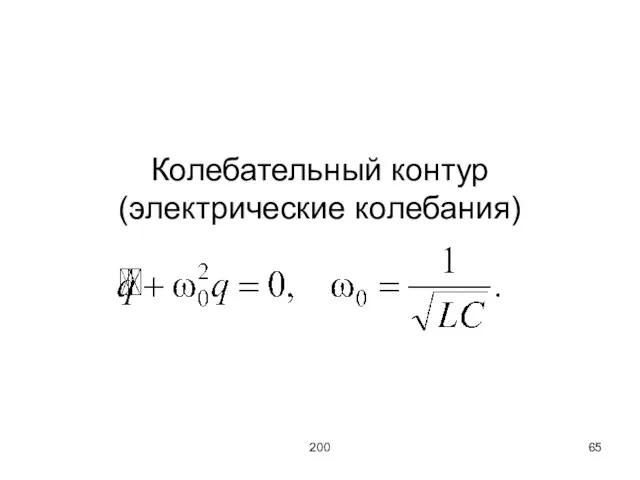
Слайд 66200
В отсутствии потерь энергии (нет диссипативных сил) выполняется закон сохранения механической энергии

– полная механическая энергия складывается из кинетической энергии грузика массой m (при прохождении положения равновесия эта энергия максимальна) и из потенциальной энергии (максимальна в крайних положениях).
Слайд 67200
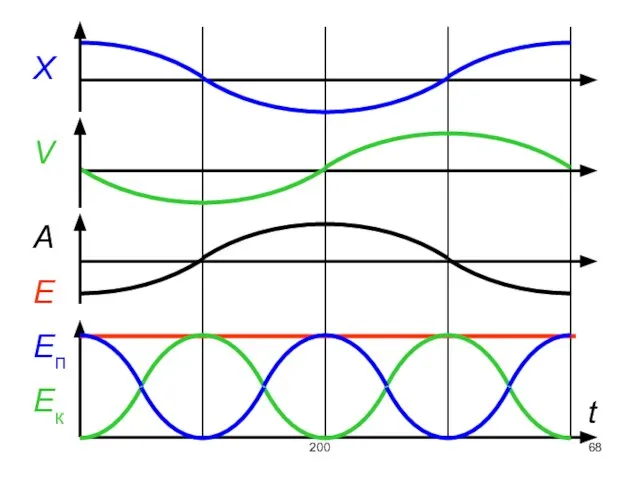
Запишем выражения для координаты, скорости, ускорения и суммарной механической энергии на примере

пружинного маятника:
Слайд 70200
ЛЕКЦИЯ № 8
Затухающие колебания.
Вынужденные колебания.

Слайд 71200
ВОПРОСЫ
26. Затухающие колебания. Время релаксации. Логарифмический декремент колебаний, добротность.
27. Вынужденные колебания. Амплитуда

и фаза вынужденных колебаний. Резонанс.
28. Связанные колебания. Нормальные координаты и нормальные моды колебаний.
Слайд 72200
26. Затухающие колебания. Время релаксации. Логарифмический декремент колебаний, добротность. Апериодические процессы.

Слайд 73200
В случае наличия сил сопротивления (трение) колебания описываются дифференциальным уравнением
β –

коэффициент затухания,
r – коэффициент сопротивления,
F = –rx – сила сопротивления.
Слайд 74200
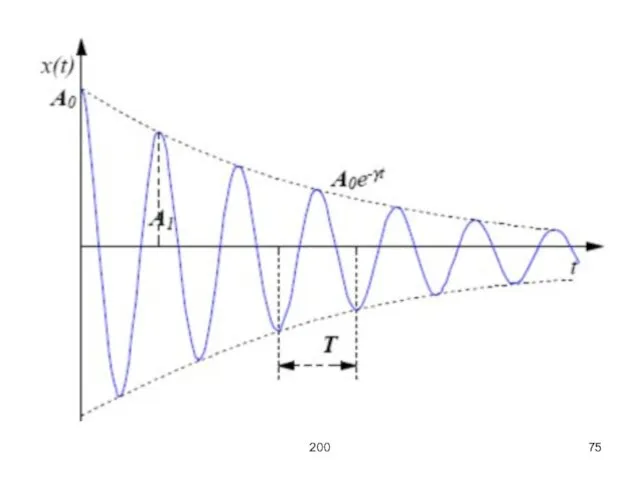
Рассмотрим случай с малым затуханием (β << ω0), в этом случае решение

уравнения имеет вид
здесь – частота затухающих колебаний, амплитуда колебаний уменьшается по экспоненте .
Слайд 76200
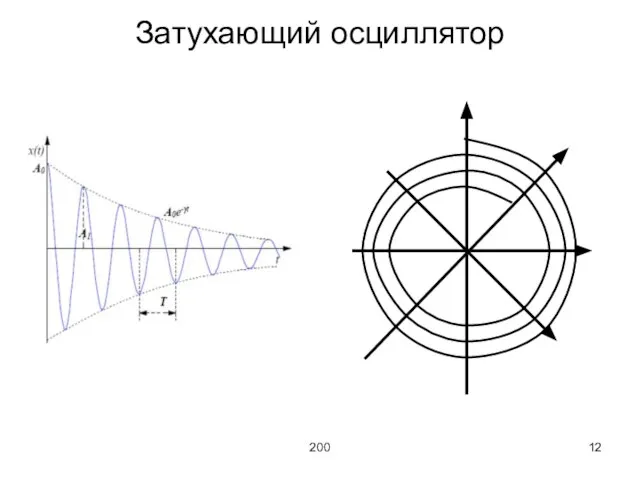
Рассмотрим характеристики затухающего колебания

Слайд 77200
Сравним значения амплитуды в моменты времени,
отличающиеся на t/:
если t/ = 1/β, то

t/ называется постоянной времени осциллятора – время, за которое амплитуда колебаний уменьшается в «е» раз.
Слайд 78200
Сравним значения амплитуды колебаний в моменты времени (t) и
(t + T):
d –

логарифмический декремент затухания. Он показывает, на сколько изменяется амплитуда колебаний за 1 период.
Слайд 79200
Например, N – число колебаний функции x(t) после которых амплитуда уменьшается в

«е» раз, тогда:
Если d = 0,01, то за N = 100 колебаний амплитуда уменьшается в «е» раз.
Слайд 80200
Добротность – это отношение средней энергии колебаний за некоторый период (E0) к

потерям энергии (ΔE) за этот же период со множителем 2π.
Слайд 81200
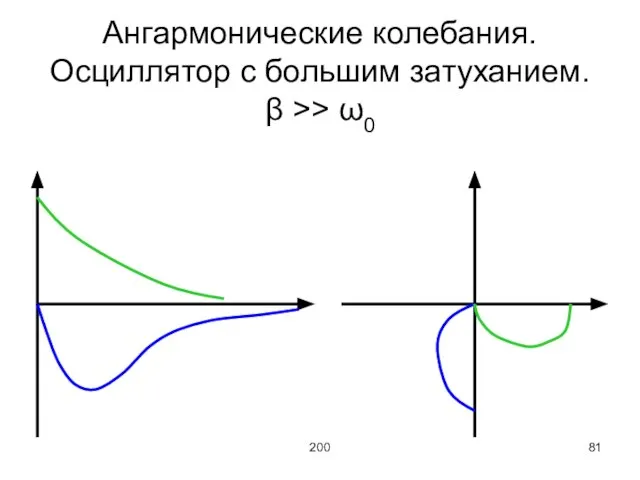
Ангармонические колебания.
Осциллятор с большим затуханием.
β >> ω0
Слайд 82200
Предельный случай β = ω0
Этот случай в технике важен тем, что при

таком соотношении параметров в случае внешнего воздействия система может вернуться в исходное состояние. (Из-за силы трения система может не вернуться в исходное положение)
Слайд 84200
27. Вынужденные колебания. Амплитуда и фаза вынужденных колебаний. Резонанс.

Слайд 85200
Если на систему действует внешняя вынуждающая сила, изменяющаяся по гармоническому закону
F =

F0cosωt, то колебание описывается уравнением
– приведённая сила.
Слайд 86200
это линейное дифференциальное неоднородное уравнение с постоянными коэффициентами. Из математики известно, что

его решением является решение общего однородного уравнения и частного решения собственно неоднородного уравнения.
Слайд 87200
Линейное дифференциальное однородное уравнение с постоянными коэффициентами второго порядка:
и его решение:

Слайд 88200
Частное решение линейного дифференциального неоднородного уравнения в комплексной форме:
Решение уравнения вынужденных

колебаний складывается из этих двух решений: x1(t) + x2(t),
но x2(t) быстро затухает и его в вынужденных колебаниях не учитывают .
Слайд 89200
Запишем решение в вещественном виде (и без x2(t)):
Амплитуда и фаза колебаний определяются

выражениями
Слайд 90200
Исследуем поведение амплитуды. При ω = 0 получаем стационарное отклонение a0 =

f0/ω0. Максимальное значение амплитуды при частоте
максимум скорости при ω = ω0, максимум ускорения при
Слайд 92200
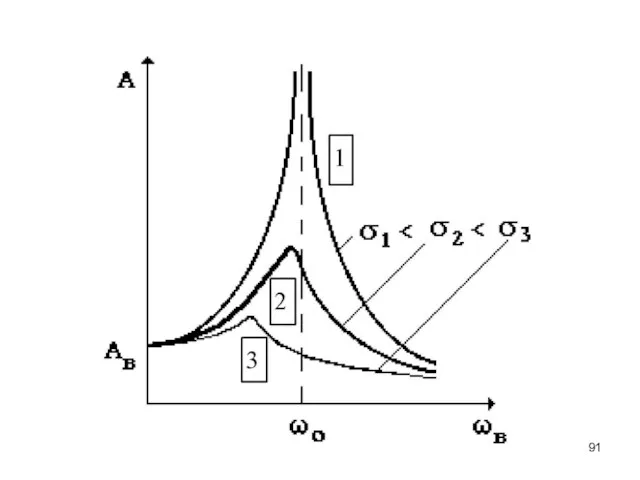
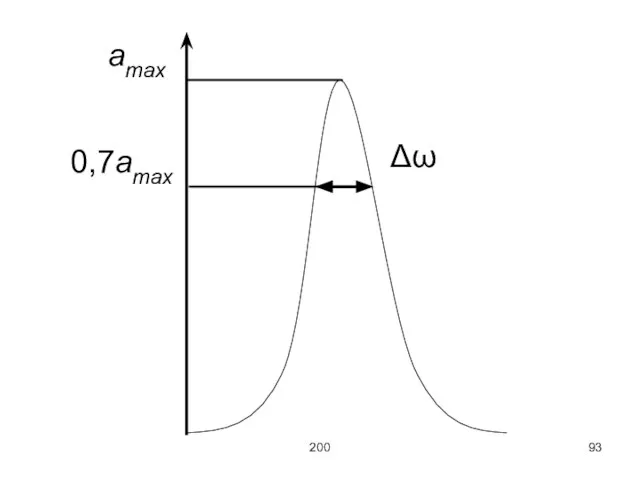
Эта кривая называется резонансной кривой. Если (в случае малых затуханий) провести горизонтальную

линию по уровню
то можно задать добротность следующим образом
Слайд 94200
Резонанс – это явление возбуждения сильных колебаний при частоте внешней возбуждающей силы,

равной частоте системы.
Но как видно из формулы резонансной частоты, резонанс достигается в случае не строгого равенства частоты собственной и частоты внешней периодической силы:
Слайд 95200
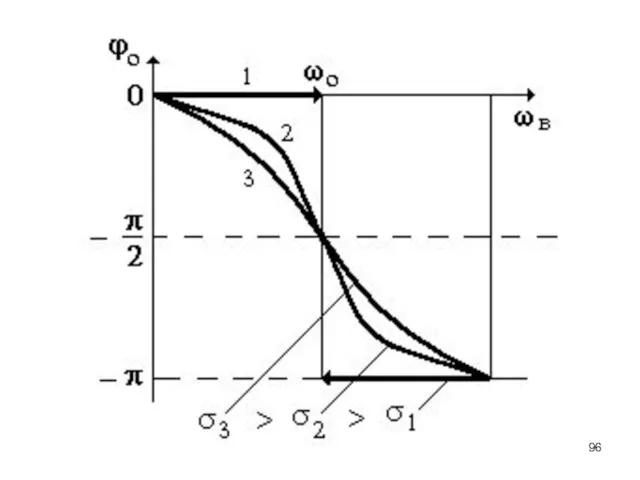
Рассмотрим фазу в случае вынужденных колебаний и в случае резонанса
рассмотрим фазовую резонансную

кривую
Слайд 97200
Параметрический резонанс
– это явление заключается в совершаемом в такт с колебаниями периодическим

изменением какого-либо параметра системы.
Слайд 98200
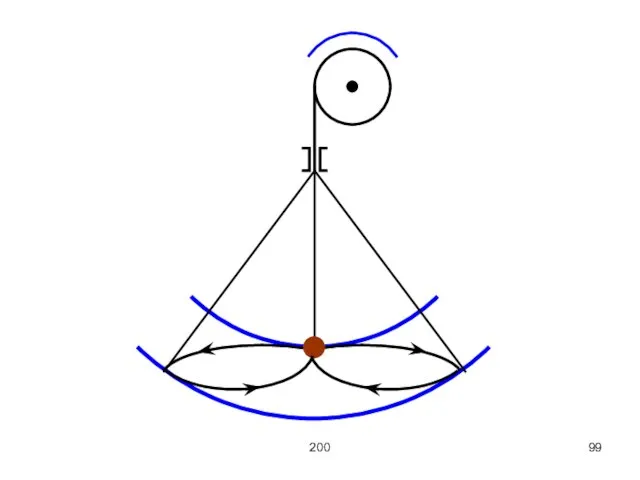
Возьмём математический маятник. Будем уменьшать длину подвеса маятника в положениях равновесия и

увеличивать в крайних положениях. В результате этого маятник будет сильно раскачиваться.
Слайд 100200
Увеличение энергии маятника происходит за счёт работы, которую совершает сила, действующая на

нить. В положениях равновесия сила натяжения нити больше, чем в крайних, поэтому прирост энергии здесь больше, чем убыль в крайних.
Слайд 102200
28. Связанные колебания. Нормальные координаты и нормальные моды колебаний.

Слайд 103200
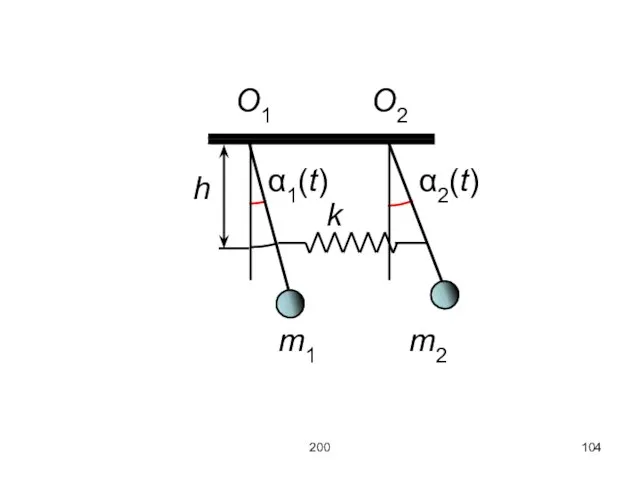
Рассмотрим закономерности поведения колебательных систем с двумя степенями свободы на следующем примере:
пусть

два маятника, связаны пружиной, будем рассматривать малые колебания, так что
sinα1 ≈ α1, sinα2 ≈ α2.
Слайд 105200
Пружина жёсткости k закреплена на расстоянии h от точек подвеса O маятников,

причём при α1= α2 = 0 пружина не деформирована.
Слайд 106200
Уравнение движения
для первого маятника имеет вид
где m1ℓ12 – момент инерции относительно оси

O1,
(–mgℓ sin α) ≈ mgℓα
– момент силы тяжести,
h(α2 – α1) – деформация (удлинение) пружины,
Слайд 107200
kh2(α2 – α1) – момент упругой силы относительно той же оси.
Аналогично,

для второго маятника
Слайд 108200
Эти два уравнения преобразуем к виду
где
собственные частоты каждого маятника.

Слайд 109200
Частоты ω01 и ω02 частоты, которые были бы, если бы не было

связи между ними.
– коэффициенты, описывающие взаимодействие маятников, обусловленное пружиной.
Слайд 110200
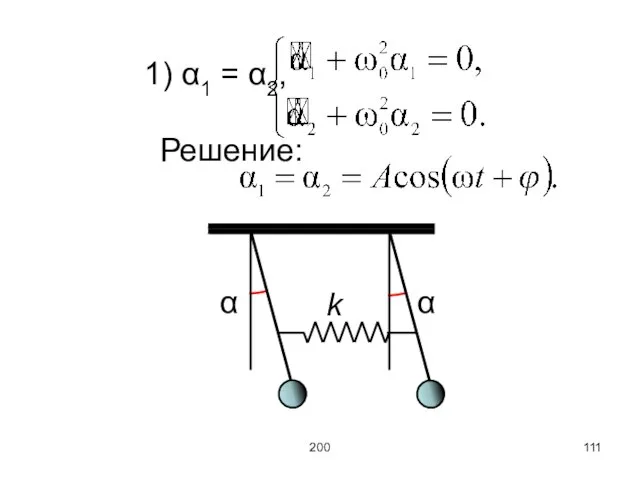
В общем случае колебания не будут гармоническими. Рассмотрим простейший случай:
ω01 =

ω02 = ω0, σ1 = σ2 = σ.
Здесь может быть два крайних случая.
Слайд 113200
Найденные решения называются нормальными колебаниями или модами.
1-я мода
2-я мода

Слайд 114200
В общем случае решение есть суперпозиция мод:
Конкретный вид этого решения зависит от

начальных условий:
A1, A2, φ1, φ2 (A1 = B1, A2 = – B2).
Слайд 115200
Другими словами, колебания осцилляторов представляют собой суперпозицию двух гармонических колебаний разных частот

ω01, ω02.
При произвольных начальных условиях колебания не являются гармоническими.
(Это решение для случая
ω01 = ω02 = ω0, σ1 = σ2 = σ.)
Слайд 118200
ВОПРОСЫ
29. Теорема Фурье.
Спектральное разложение. Принцип радиосвязи.
30. Ангармонические колебания. Автоколебания.

Слайд 119200
29. Теорема Фурье.
Спектральное разложение. Принцип радиосвязи.

Слайд 120200
Теорема Фурье: Любая периодическая функция может быть разложена преобразованием Фурье, то есть

представлена в виде суммы конечного или бесконечного числа синусоидальных и/или косинусоидальных функций.
Слайд 121200
Запишем ряд Фурье в комплексной форме:
здесь f(t) – периодическая функция, Ck –

коэффициенты, i – мнимая единица, ωk – частоты, соответствующие коэффициентам Ck, ωk = k·Ω, k = 0, 1, 2, … ,
Ω – основная частота.
Слайд 122200
Для вычисления Ck умножим обе части на и проинтегрируем:
если k ≠ m,

то интеграл справа равен 0, если k = m, то период Т. Отсюда
Слайд 123200
В тригонометрическом виде теорема Фурье выглядит следующим образом

Слайд 124200
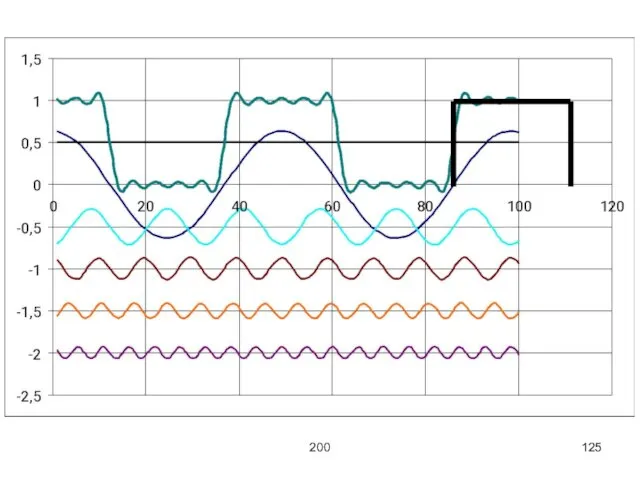
Пример: Рассмотрим разложение периодической чётной функции (в разложении будут только косинусы) с

использованием первых десяти членов (a0, a1, a3, a5, a7, a9 ≠ 0;
a2, a4, a6, a8 = 0).
Слайд 126200
Модулированное колебание
здесь A(t) – амплитудная модуляция, ω(t) – частотная модуляция,
φ(t) – фазовая

модуляция.
Слайд 127200
Рассмотрим синусоидальную модуляцию:
A0, α, Ω – const, ω – несущая частота, α

– глубина модуляции,
Ω – частота модуляции.
Слайд 128200
Получаем в итоге колебание на трёх частотах:
С помощью гармонического осциллятора можно выделить

одну из частот, совпадающую с его собственной ω.
Слайд 129200
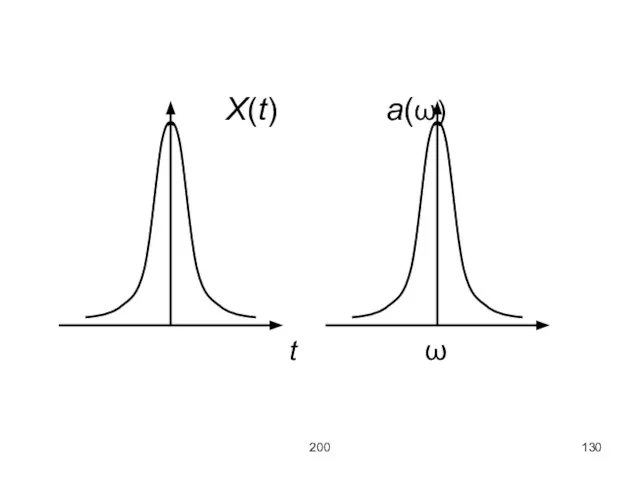
Теорема Фурье для непериодической функции X(t):
Здесь имеет место непрерывное множество синусоидальных колебаний,

частоты которых непрерывно заполняют определённый интервал.
Слайд 131200
Принцип радиосвязи
Человеческое ухо воспринимает частоту 20 – 20000 Гц, но для передачи

такого сигнала нужны гигантские антенны
L = λ/2 = c/2ν ~ 105 м.
λ – длина волны, c – скорость света, ν – частота.
Слайд 132200
Для передачи используют радиоволны на частотах 105 – 108 Гц и даже

на частотах 1010 Гц.
Сигнал модулируют низкой частотой (звуковая частота), а передают на высокой частоте (радиоволны).
Слайд 133200
Модуляция может быть амплитудной, фазовой, частотной.
Пример амплитудной модуляции
(f(t) – модулирующая функция):

Слайд 134200
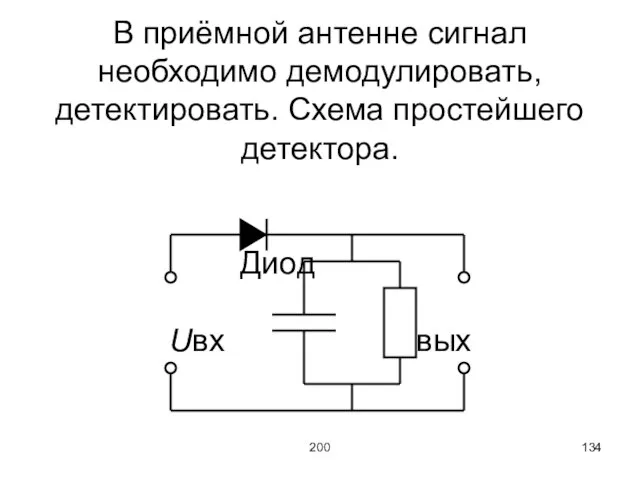
В приёмной антенне сигнал необходимо демодулировать, детектировать. Схема простейшего детектора.
Диод
Uвх Uвых
Слайд 135200
1) сигнал 3) сигнал после детектора (диода)
2) модулирующий 4) детектированный сигнал сигнал на
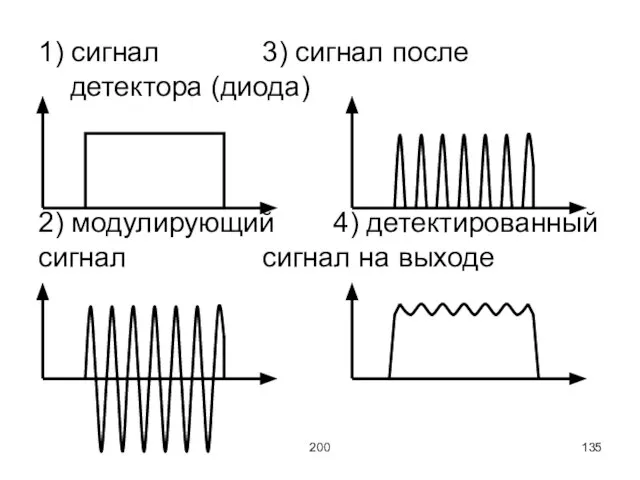
выходе
Слайд 137200
30. Ангармонические колебания. Автоколебания.

Слайд 138200
Ангармонические колебания
Уравнение динамики математического маятника имеет вид:
В случае малых отклонений
(α ≈ sin

α) колебания можно считать гармоническими:
Слайд 139200
Именно в этом случае, в случае гармонических колебаний, период не зависит от

амплитуды колебаний.
Возвращающая сила прямо пропорциональна смещению:
Слайд 141200
В случае не малых отклонений
колебания перестают быть гармоническими: сила нелинейно зависит от

смещения
Слайд 142200
В этом случае период зависит от амплитуды.
Примеры: маятник с большими отклонениями, пружинный

маятник с переменной жёсткостью, колебательный контур, в катушке которого сердечник, при больших амплитудах.
Слайд 143200
Автоколебания
Вынужденные незатухающие колебания в реальных системах, период и амплитуда которых не зависит

от характера внешнего воздействия, а определяется свойствами самой автоколебательной системы.
Слайд 144200
Автоколебательные системы – системы, способные совершать незатухающие колебания в отсутствие периодического внешнего

воздействия.
Слайд 145200
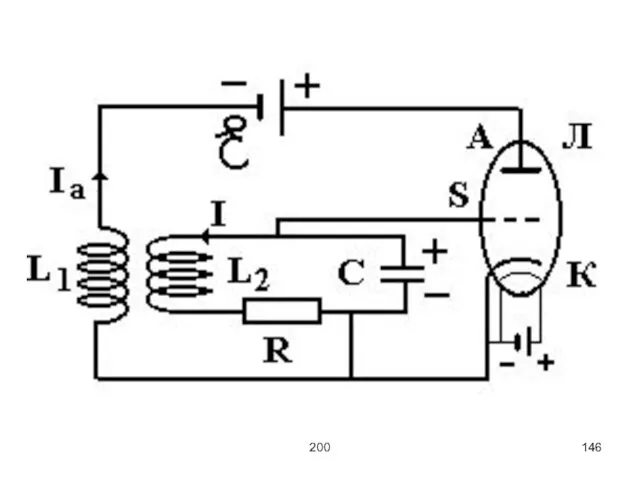
Кратко рассмотрим возникновение автоколебаний на примере лампового генератора электромагнитных колебаний, где Л

– лампа-триод, S – сетка, А – анод, К – катод, L2 – индуктивность, R – сопротивление, C – ёмкость, L1 – катушка обратной связи, Ԑ − ЭДС источника тока.
Слайд 147200
При разряде конденсатора через лампу будет течь анодный ток Ia, а потенциал

сетки упадет, что приведет к уменьшению анодного тока.
Если витки катушек намотаны параллельно, то за счет взаимной индукции затухание в контуре увеличится.
Возникнет отрицательная обратная связь.
Слайд 148200
Если же витки катушек намотаны антипараллельно, то затухание в контуре уменьшится, амплитуда

колебаний начнет возрастать.
Возникнет положительная обратная связь.
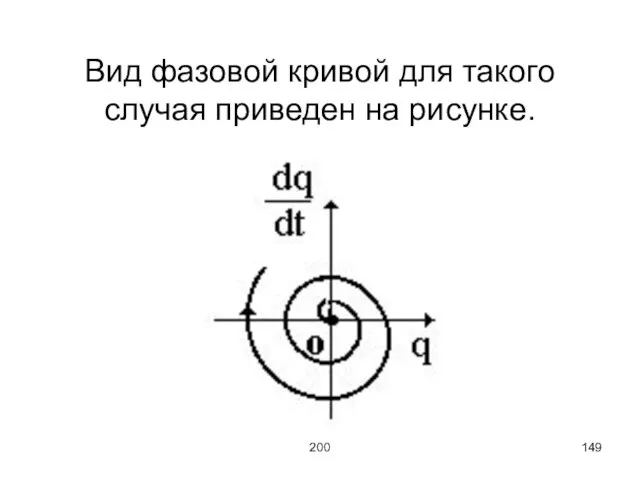
Слайд 149200
Вид фазовой кривой для такого случая приведен на рисунке.
Слайд 150200
Уравнение для данного контура можно записать в виде:
q – заряд на обкладках

конденсатора.
Слайд 151200
M, S = const, S – крутизна сеточной характеристики; М – коэффициент

взаимной индукции,
колебания в автоколебательном контуре будут подчиняться закону:
Слайд 152200
Если выполняется условие -SM / C > R (δ < 0), то

состояние равновесия будет неустойчивым фокусом.
Любое малое отклонение системы от равновесия будет возрастать.
Колебательный контур начнет самовозбуждаться.
Слайд 153200
В контуре устанавливаются автоколебания с постоянной амплитудой, которая не зависит от начальных

условий, а определяется параметрами системы.
Это есть общее свойство всех автоколебательных систем.
Слайд 154200
Рол нелинейности.
Амплитуда автоколебаний от начальных условий не зависит.
Автоколебания могут возбуждаться периодическими внешними

силами, но период автоколебаний не зависит от периода этих сил.
Слайд 155200
Релаксационные колебания – это колебания, которые происходят под действием постоянной вынуждающей силы

за счёт перехода системы из одного состояния в другое (пример: ветер и дерево). Параметрические колебания – колебания за счёт изменения параметра системы.
Слайд 158200
ВОПРОСЫ
31. Волны. Типы и характеристики волн. Волновое уравнение и уравнение плоской

бегущей волны. Стоячие волны (вывод).
32. Упругие волны. Энергия волны. Вектор Умова.
33. Поведение звука на границе раздела двух сред. Ударные волны. Эффект Доплера.
Слайд 159200
Вопрос № 26.
31. Волны. Типы и характеристики волн. Волновое уравнение и

уравнение плоской бегущей волны. Стоячие волны (вывод).
Слайд 160200
Волна – процесс распространения колебаний в пространстве с течением времени.
Таким образом, волна

это некоторая функция S = S(x, y, z, t).
Эту функцию можно представить в следующем виде:
S(z, t) = S(z – vt)
– распространение волны вдоль оси Z.
Слайд 161200
Волновое уравнение (пространственное и вдоль оси Z)
оператор Лапласа

Слайд 162200
Рассмотрим плоскую монохроматическую волну (на одной частоте)
S(z, t) = a cos(ωt

– kz)z.
ω – циклическая частота волны,
k = 2π/λ = ω/ʋ – волновой вектор,
ʋ = ω/k = λω/2π – фазовая скорость,
λ – длина волны,
Т – период,
(ωt – kz) – фаза волны.
Слайд 163200
Для плоской бегущей волны S и фаза одинаковы, синфазны, в любой точке

(x, y) плоскости z = const.
Поверхности, где колебания синфазны, называются волновыми поверхностями.
Поверхность, до которой дошла волна в данный момент времени, называется волновым фронтом.
Слайд 164200
Волновой вектор показывает направление распространения волны
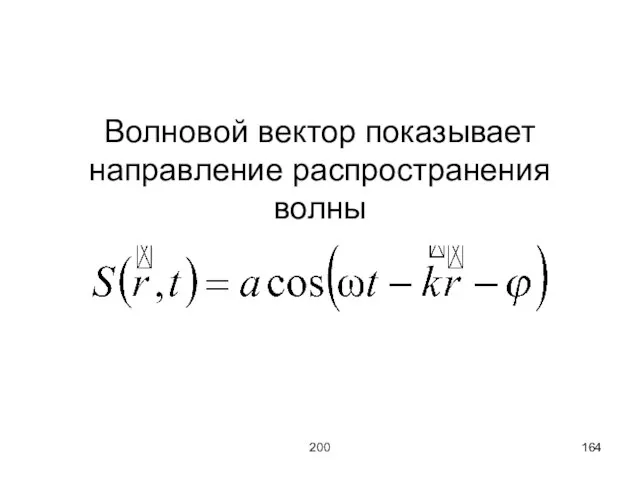
Слайд 165200
Стационарные волны – волновая функция постоянна.
Синусоидальная волна – колебания в некоторой точке

пространства происходят по закону синуса.
Скалярные волны – волновое возмущение описывается скалярной величиной (плотность, давление).
Векторные волны – волновое возмущение описывается векторной величиной (напряжённость)
Слайд 166200
Продольные волны – колеблющая величина совершает колебания параллельно волновому вектору (вдоль направления

распространения волны ),
Поперечные волны – колеблющая величина совершает колебания перпендикулярно волновому вектору (поперёк направления распространения волны )
Слайд 167200
Плоскополяризованная волна – волна, колебания в которой вектора S происходят в фиксированной

плоскости. Эта плоскость называется плоскостью поляризации.
Слайд 168200
Стоячие волны
Рассмотрим сложение двух волн:
S1(z, t) = acos(ωt – kz),
S2(z, t) =

acos(ωt + kz),
одна волна падающая (вектор – k),
другая волна отражённая от какой-либо преграды (вектор + k).
Слайд 169200
В результате сложения падающей и отражённой волны получаем выражение:
S1 + S2

= 2a cos(kz) cos(ωt).
Временные и пространственные коэффициенты оказались разделены. Это выражение описывает волну, у которой нет перемещения волновых поверхностей. Это и есть стоячие волны.
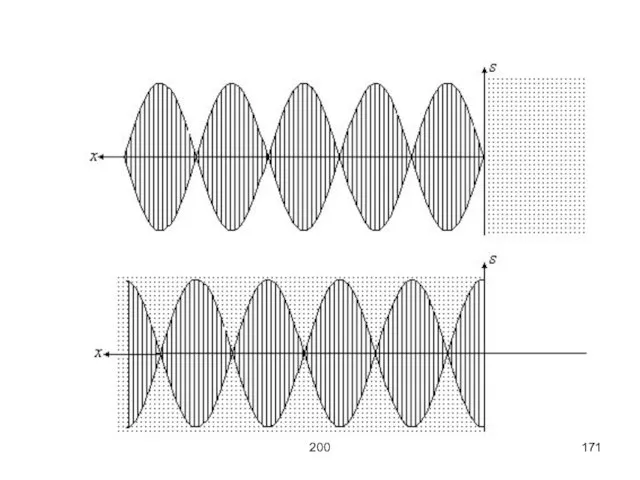
Слайд 170200
Если волна отражается от среды менее плотной, чем среда распространения, то сдвига

фаз в волне не происходит. В этой точке у стоячих волн всегда максимум амплитуды – пучность.
Если волна отражается от более плотной среды, то происходит сдвиг фазы на пол длины волны. В этой точке у волны узел – нулевая амплитуда.
Слайд 173200
32. Упругие волны. Энергия волны. Вектор Умова.

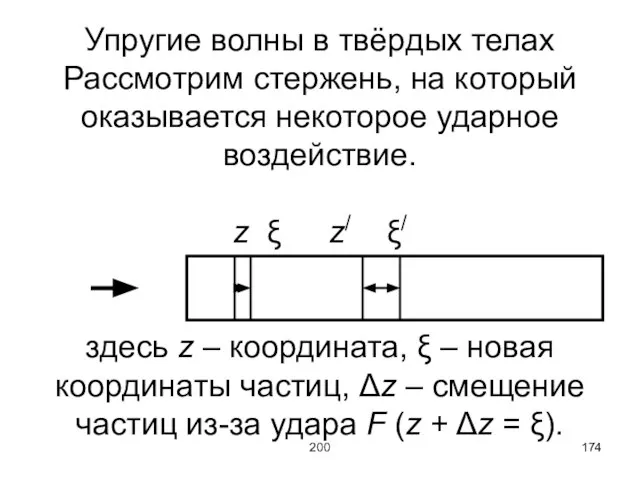
Слайд 174200
Упругие волны в твёрдых телах
Рассмотрим стержень, на который оказывается некоторое ударное воздействие.
z
ξ z/ ξ/
F
здесь z – координата, ξ – новая координаты частиц, Δz – смещение частиц из-за удара F (z + Δz = ξ).
Слайд 175200
Продольная деформация
dz – расстояние между точками без напряжения, dξ – расстояние между

точками при деформации (из-за распространения волны).
Слайд 176200
Сами частицы стержня смещаются незначительно, приводя в движение соседние частицы, те передают

импульс соседним частицам и т.д. – именно так малые смещения частиц приводят к распространению волнового возмущения на большие расстояния.
Слайд 177200
Волновое уравнение упругих деформаций
ʋ2 = E/ρ0 – скорость волны, E – модуль

Юнга, ρ0 – плотность вещества без нагрузки.
Слайд 178200
Упругие волны в газах и жидкостях
Волна в газах или жидкостях распространяется за

счёт изменения давления и плотности.
Волновое уравнение
ξ – смещение центра масс участка среды.
Слайд 179ξ
200
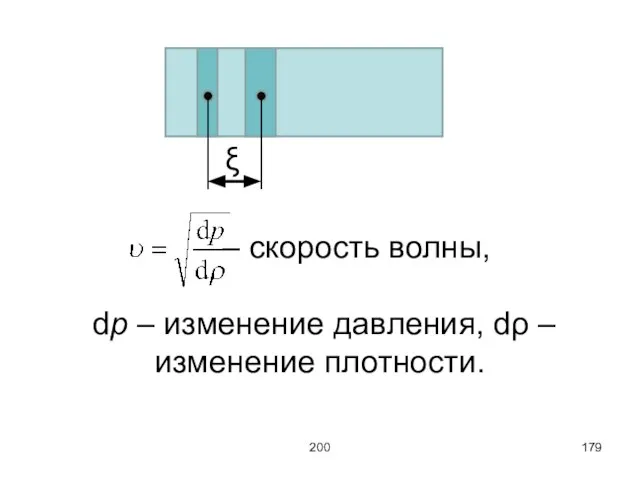
– скорость волны,
dp – изменение давления, dρ – изменение плотности.
Слайд 180200
Для газов
p0 – давление в обычных условиях, ρ0 –плотность в обычных

условиях,
γ – показатель адиабаты, Cp, CV – теплоёмкости при постоянном давлении и объёме
1 моля газа, соответственно.
Слайд 181200
Энергия волны
В упругой волне энергия складывается из кинетической и потенциальной составляющих.
Объёмная плотность

энергии
Слайд 182200
Волновой процесс представляет собой передачу энергии без передачи вещества.
Введём вектор – плотность

потока энергии (вектор Умова-Пойтинга):
σ = Eε – напряжение, n – единичный вектор, который направлен так же как и направление бегущей волны.
Слайд 183200
В газе или жидкости
Поток энергии через площадку S за время dt:

Слайд 185200
33. Поведение звука на границе раздела двух сред. Ударные волны. Эффект Доплера.

Слайд 186200
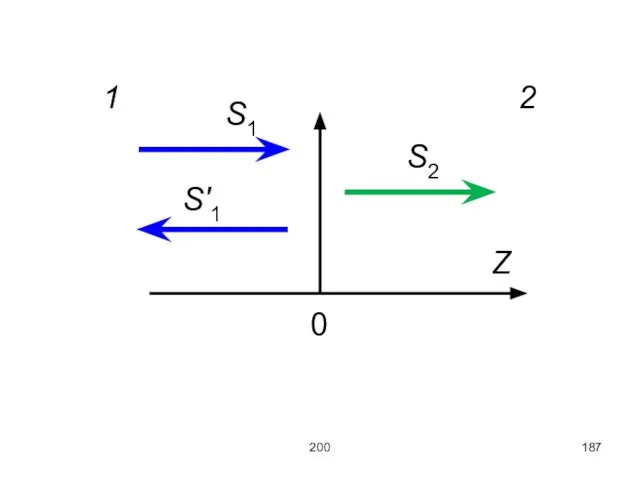
Поведение звука границе раздела двух сред.
Рассмотрим плоскую звуковую волну
S1 = a1

cos(ωt – k1z),
в области 1 z < 0.
На границе раздела (z = 0) волна разделяется на две:
прошедшую (S2) и отражённую (S′1).
Слайд 188200
Прошедшая волна
S2 = a2 cos(ωt – k2z),
отражённая волна
S′1 = a′1 cos(ωt

+ k1z),
k1 ≠ k2, ʋ1 ≠ ʋ2.
Слайд 189200
Запишем граничные условия:
E1k1(a1 – a′1) = E2k2a2.
Это условие получено из условия

равенства сил, действующих на границе со стороны одной среды на другую.
Слайд 191200
Порог слышимости (минимальная слышимая интенсивность звука)
I0 ≈ 10–12 Вт/м2,
Болевой порог
I ≈ 1012

I0.
Интенсивность звука выражают в децибелах:
β = 10log I/I0, 1010 I0 ÷ β = 100 дБ,
порог слышимости β0 = 0 дБ,
болевой порог β = 120 дБ.
Слайд 192200
Ударные волны
В случае малых возмущений среда линейна – волна синусоидальна. С ростом

амплитуды возмущения среда теряет линейность, волна становится не синусоидальной. Участки с большим возмущением имеют большую скорость. Возникают волны различных частот. В этом случае говорят о взрывной волне.
Слайд 193200
Эффект Доплера – изменение частоты излучения при относительном движении источника и приёмника

(верхний знак относится к сближению, нижний – к расхождению)
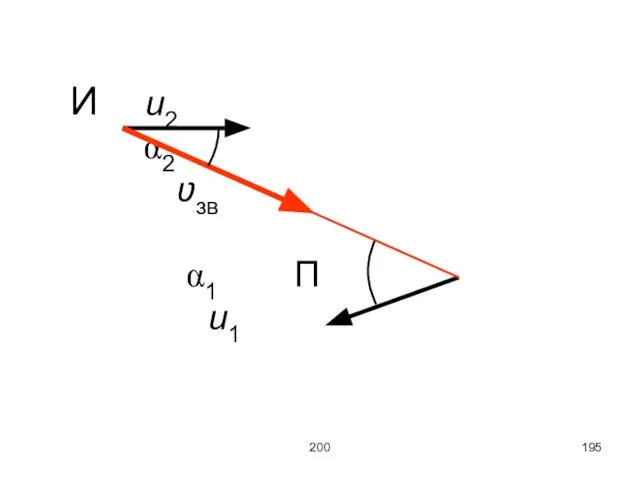
Слайд 194200
Здесь ν – частота принимаемого сигнала, ν0 – частота испускаемого сигнала, ʋзв

– скорость сигнала (звукового или светового), u1 – скорость приёмника, u2 – скорость источника, α1 – угол между направлением на источник и движением приёмника, α2 – угол между направлением на приёмник и направлением движения источника.

































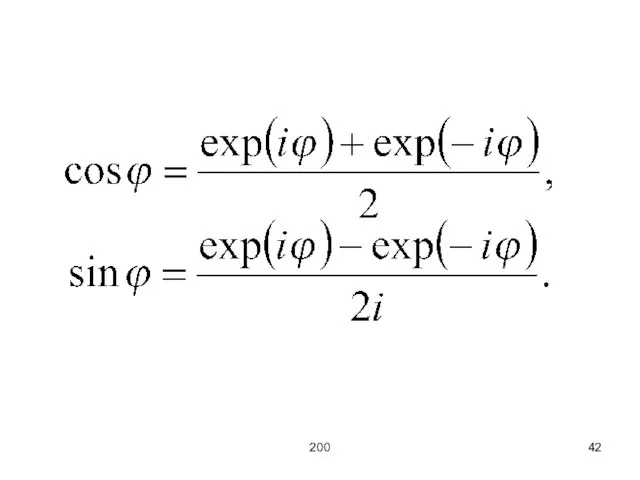



















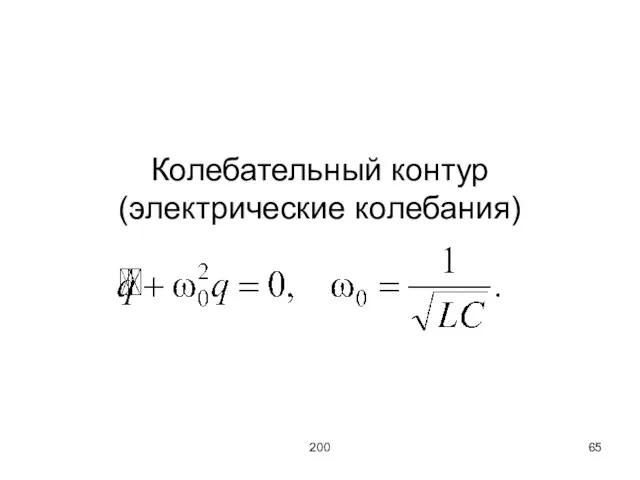






































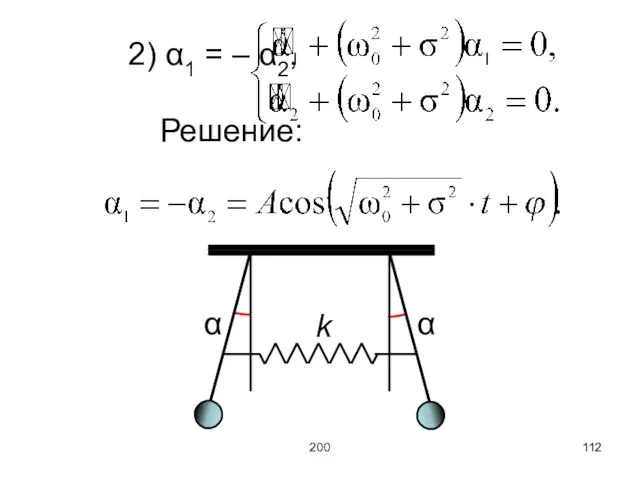















































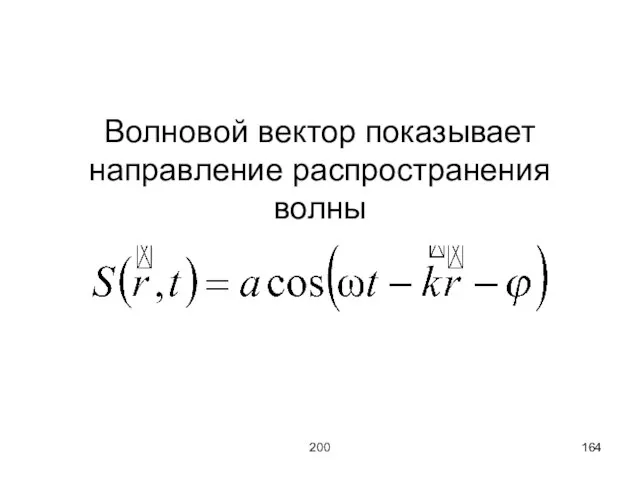




























 Магнитное поле. Действие магнитного поля на проводник с током
Магнитное поле. Действие магнитного поля на проводник с током Презентация на тему Движение тела, брошенного вертикально вверх
Презентация на тему Движение тела, брошенного вертикально вверх  Плавание тел. Воздухоплавание
Плавание тел. Воздухоплавание Игра-КВН Первый урок в 8 классе
Игра-КВН Первый урок в 8 классе Пространственная система сил
Пространственная система сил Основные понятия кинематики
Основные понятия кинематики Теория ядерных реакторов. Семинар к курсовому проекту по спецкурсу № 2
Теория ядерных реакторов. Семинар к курсовому проекту по спецкурсу № 2 Фізичні та хімічні явища
Фізичні та хімічні явища Физические величины и единицы измерения. Лабораторная работа 1
Физические величины и единицы измерения. Лабораторная работа 1 Презентация на тему Интерференция волн
Презентация на тему Интерференция волн  Презентация на тему Виды сил
Презентация на тему Виды сил  Техническое обслуживание и ремонт подшипников электрических машин
Техническое обслуживание и ремонт подшипников электрических машин 21 061
21 061 Дисперсные системы
Дисперсные системы Атомная энергетика. Реакторы
Атомная энергетика. Реакторы Электрические цепи и их элементы
Электрические цепи и их элементы Физика на службе человека
Физика на службе человека Метод расчета сложных электрических цепей
Метод расчета сложных электрических цепей Решение задач на расчет полного сопротивления цепи
Решение задач на расчет полного сопротивления цепи Сила скрученной резины. (2 класс)
Сила скрученной резины. (2 класс) Мирный атом
Мирный атом Плазма и её использование
Плазма и её использование Переменный ток
Переменный ток Явление электромагнитной индукции
Явление электромагнитной индукции Преобразование механической энергии в электрическую и обратно. Лекция 2
Преобразование механической энергии в электрическую и обратно. Лекция 2 Автосцепное устройство
Автосцепное устройство Вихрь (ротор) векторного поля
Вихрь (ротор) векторного поля