Содержание
- 2. Цель лекции – ознакомиться с методами количественного описания суперпозиции гармонических колебаний и их практическим применением. Вопросы
- 3. 23.4. Геометрические способы представления гармонических колебаний. Сложение колебаний – это нахождение закона результирующего колебания системы в
- 4. 1) Метод векторных диаграмм (метод вращающего вектора амплитуды) Правила построения: 1. Задаем ось Os, вдоль которой
- 5. 2) Метод комплексного представления Правила построения: 1. Значение переменной величины s задается точкой на комплексной плоскости:
- 6. ► оба метода базируются на общем (геометрическом) способе представления колебаний и взаимно дополняют друг друга; Замечания:
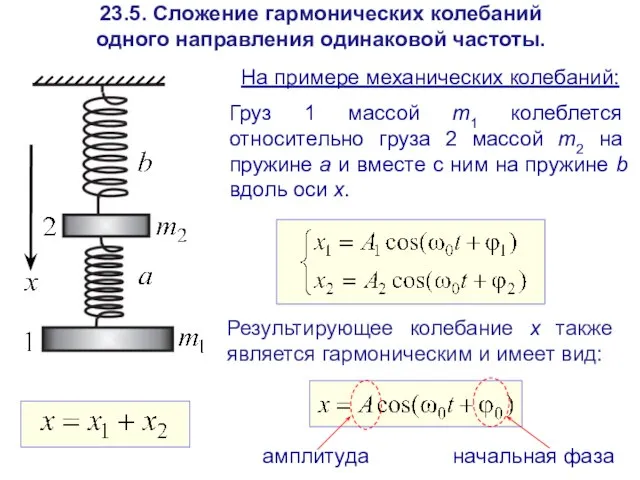
- 7. 23.5. Сложение гармонических колебаний одного направления одинаковой частоты. Груз 1 массой m1 колеблется относительно груза 2
- 8. Амплитуда А результирующего колебания разность фаз (23.18) Начальная фаза ϕ0 результирующего колебания (определяется через отношение суммы
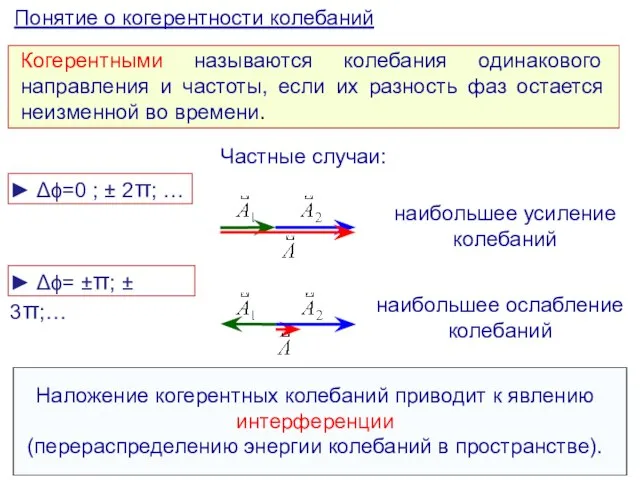
- 9. Понятие о когерентности колебаний Когерентными называются колебания одинакового направления и частоты, если их разность фаз остается
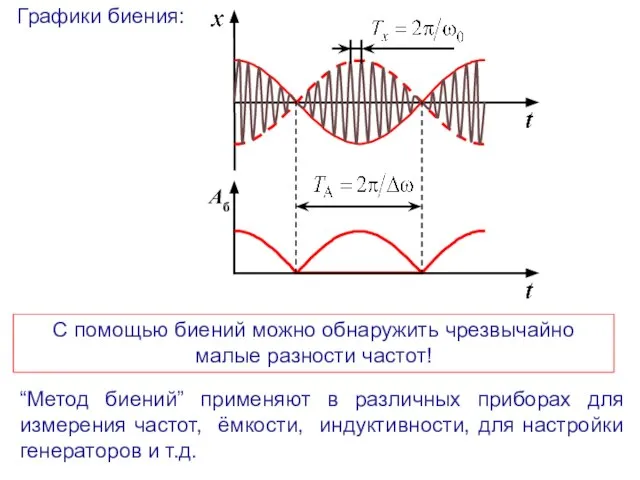
- 10. Понятие о биениях Биения – это результат сложения гармонических колебаний одинакового направления близких частот Для простоты
- 11. По формуле суммы косинусов: (23.20) уравнение биений, которые можно рассматривать как гармоническое колебание с пульсирующей амплитудой.
- 12. Графики биения: “Метод биений” применяют в различных приборах для измерения частот, ёмкости, индуктивности, для настройки генераторов
- 13. 23.6. Сложение взаимно перпендикулярных колебаний одинаковой частоты. Уравнение траектории результирующего колебания находится исключением параметра t: На
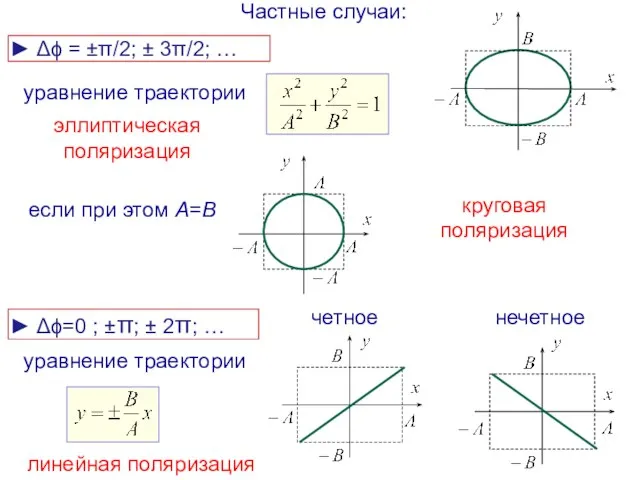
- 14. Траектория результирующего колебания: плоскость колебаний (23.22) Вектор амплитуды за один период описывает в плоскости колебаний эллипс:
- 15. Частные случаи: ► Δϕ=0 ; ±π; ± 2π; … ► Δϕ = ±π/2; ± 3π/2; …
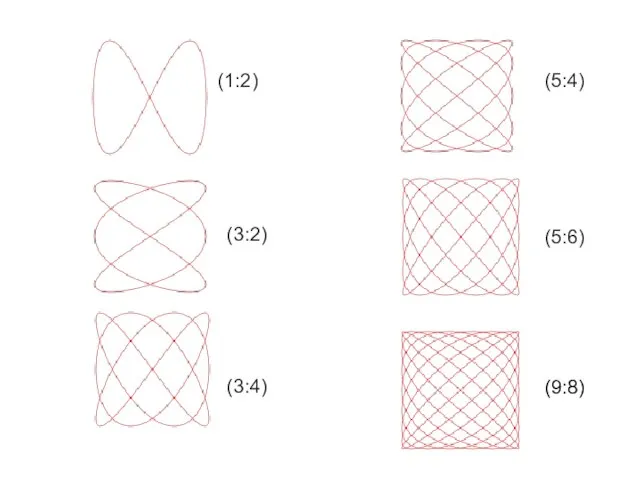
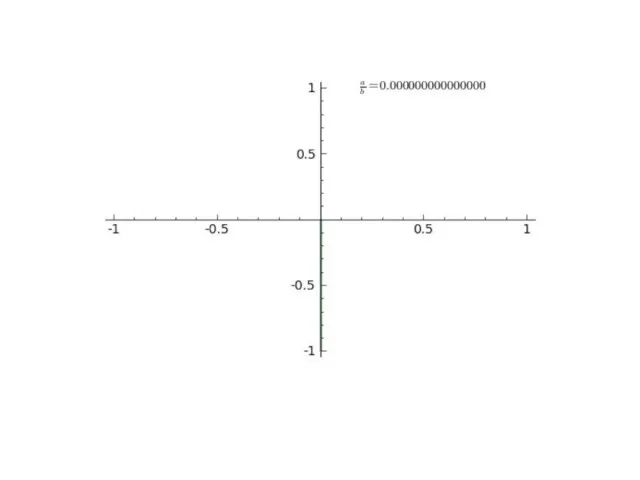
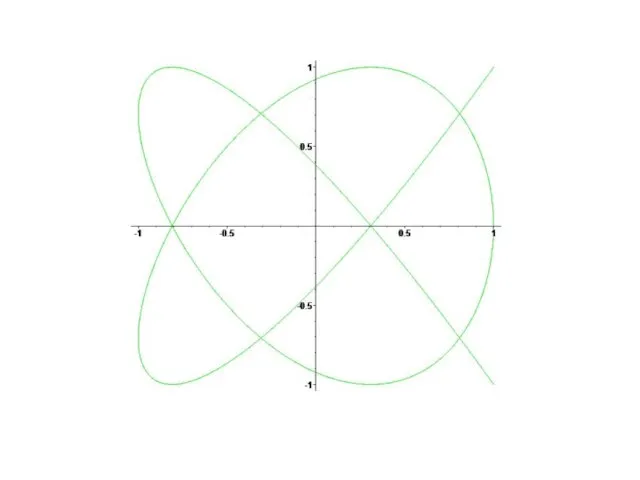
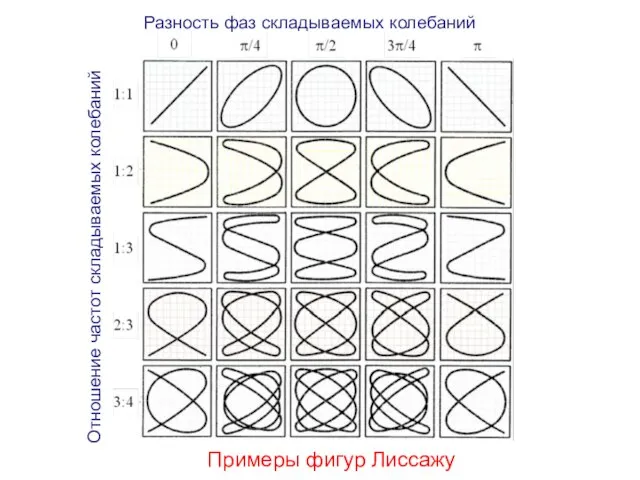
- 17. 23.7. Сложение взаимно перпендикулярных колебаний разных частот. Фигуры Лиссажу. Если взаимно перпендикулярные колебания происходят с циклическими
- 18. Пусть отношение частот взаимно перпендикулярных колебаний равно 1:2 и разность фаз Δϕ = π/2. Уравнения колебаний
- 19. (1:2) (3:2) (3:4) (5:4) (5:6) (9:8)
- 22. Отношение частот складываемых колебаний Разность фаз складываемых колебаний
- 24. Скачать презентацию













 К решению задач на зарядку конденсатора
К решению задач на зарядку конденсатора Магнитодиэлектрический эффект в нанокристаллическом мультиферроике BiFeO3
Магнитодиэлектрический эффект в нанокристаллическом мультиферроике BiFeO3 Система охлаждения двигателя
Система охлаждения двигателя Полимерные композиционные материалы – исходные компоненты и их свойства. Лекция 2
Полимерные композиционные материалы – исходные компоненты и их свойства. Лекция 2 Зубчатые передачи
Зубчатые передачи Skaņa
Skaņa Презентация на тему Потенциальная энергия
Презентация на тему Потенциальная энергия  Механик тирбәнеш, дулкыннар. Тавыш
Механик тирбәнеш, дулкыннар. Тавыш Основные понятия о точности и взаимозаменяемости
Основные понятия о точности и взаимозаменяемости Ветрогенератор-фонарь
Ветрогенератор-фонарь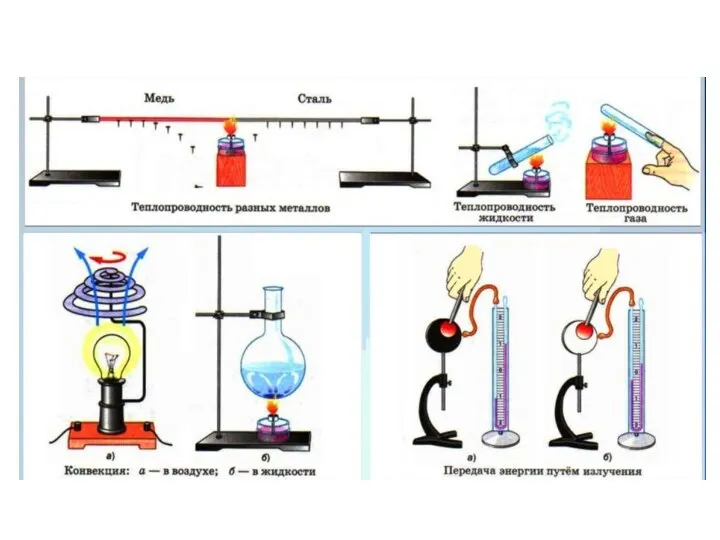 Vidy_teploperedachi
Vidy_teploperedachi Магнитные явления
Магнитные явления САУ нагревательной установки (СПУ)
САУ нагревательной установки (СПУ)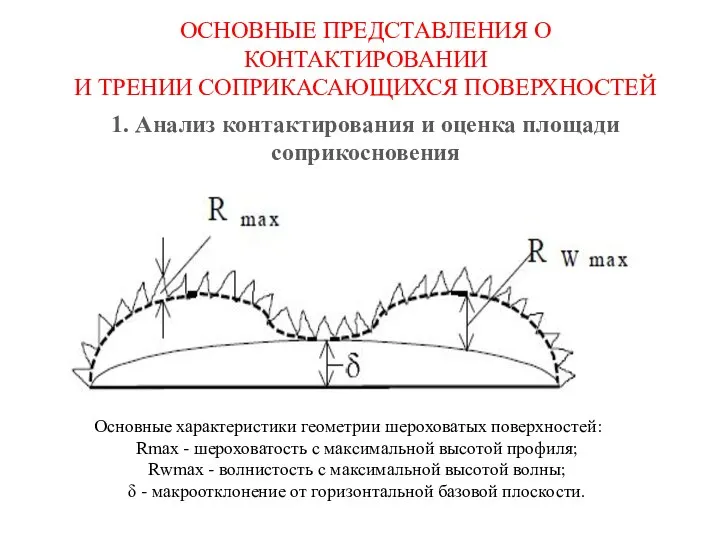 Основные представления о контактировании и трении соприкасающихся поверхностей
Основные представления о контактировании и трении соприкасающихся поверхностей Решение задач на закон Ома
Решение задач на закон Ома Основные положения молекулярно - кинетической теории
Основные положения молекулярно - кинетической теории Изображения, даваемые линзой
Изображения, даваемые линзой Механика. Лекция 2
Механика. Лекция 2 Подъемные механизмы
Подъемные механизмы Рамка с током в однородном магнитном поле
Рамка с током в однородном магнитном поле Механический и магнитный моменты атома
Механический и магнитный моменты атома Определение показателя преломления стекла
Определение показателя преломления стекла HSC & HRD
HSC & HRD Магнетизм. Структурно-логическая схема. Условные обозначения
Магнетизм. Структурно-логическая схема. Условные обозначения Тепловые двигатели
Тепловые двигатели Использование наноматериалов в технике
Использование наноматериалов в технике Колебания. Общие понятия
Колебания. Общие понятия Явление электромагнитной индукции
Явление электромагнитной индукции