Содержание
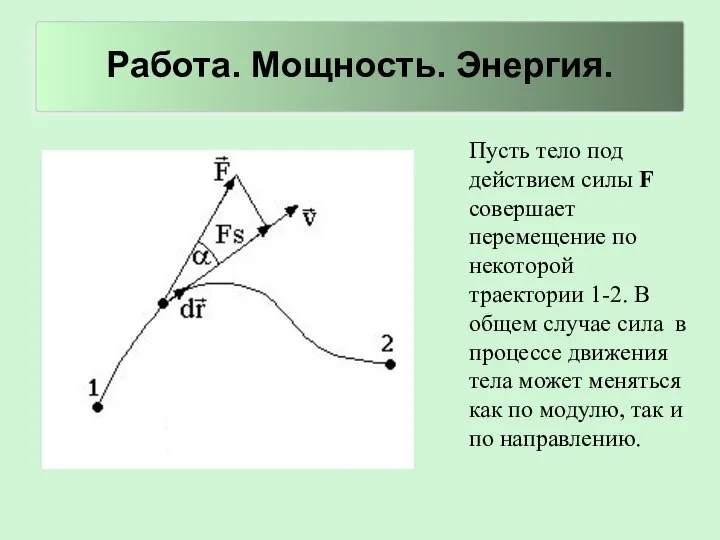
- 2. Работа. Мощность. Энергия. Пусть тело под действием силы F совершает перемещение по некоторой траектории 1-2. В
- 3. Рассмотрим элементарное перемещение, в пределах которого силу можно считать постоянной. Элементарной работой силы на перемещении называется
- 4. Суммируя (интегрируя) выражение по всем элементарным участкам пути от точки 1 до точки 2, найдем работу
- 5. Если сила имеет постоянные величину и направление, то вектор в выражении для работы можно вынести за
- 6. Единица работы – джоуль (Дж). 1 Дж – работа, совершаемая силой 1 Н на пути 1м
- 7. Для характеристики скорости, с которой совершается работа, вводят величину, называемую мощностью. Мощность – это работа, совершаемая
- 8. Учитывая, что , получим Таким образом, мощность, развиваемая силой , равна скалярному произведению вектора силы на
- 9. Мощность – скалярная величина. Единица мощности – ватт (Вт): 1 Вт – мощность при которой за
- 10. Существуют различные формы движения материи – механическая, тепловая, электромагнитная, ядерная и др. В одних явлениях форма
- 11. В механике различают два вида энергии – кинетическую и потенциальную. Кинетическая энергия – это механическая энергия
- 12. Таким образом, То есть работа силы идет на приращение некоторой величины (стоящей в скобках). Эту величину
- 13. При конечном перемещении из точки 1 в точку 2 работа силы идет на приращение кинетической энергии:
- 14. Потенциальная энергия – это механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия
- 15. Пусть взаимодействие между телами осуществляется с помощью силовых полей (например, поле гравитационных сил, поле упругих сил),
- 16. Тело, находящееся в поле консервативных сил, обладает потенциальной энергией EП. Работа консервативной силы определяется разностью потенциальной
- 17. Работа консервативных сил на конечном участке пути 1 – 2 Потенциальная энергия – функция, которая определяется
- 18. Конкретный вид функции EП зависит от характера силового поля. Например, потенциальная энергия тела массы m, поднятого
- 19. Потенциальной энергией может обладать не только система тел, но и отдельно взятое упруго деформированное тело –
- 20. При возвращении пружины из деформированного в недеформированное состояние сила упругости совершает работу Если потенциальную энергию пружины
- 21. Полная механическая энергия системы E=EK + EП , т.е. равна сумме кинетической и потенциальной энергий
- 22. Связь между потенциальной энергией и силой. Потенциальная энергия тела зависит от его координат: EП = EП
- 23. Рассмотрим перемещение тела под действием силы F. Разложим силу на три составляющие вдоль координатных осей и
- 24. Эту работу можно представить как убыль потенциальной энергии: Из сравнения последних выражений имеем: Отсюда Здесь -
- 25. Такие производные называются частными и обозначаются символом Итак, Эти три формулы можно объединить в одну векторную
- 26. Или Выражение, стоящее в скобках, называют градиентом функции и обозначают Сила равна градиенту потенциальной энергии, взятому
- 27. Потенциальные кривые. Условия равновесия механической системы. Рассмотрим материальную точку, положение которой может быть определено с помощью
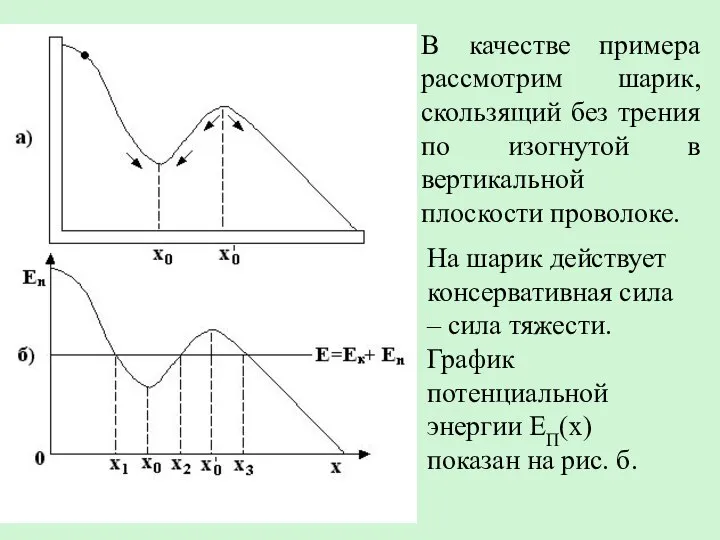
- 28. В качестве примера рассмотрим шарик, скользящий без трения по изогнутой в вертикальной плоскости проволоке. На шарик
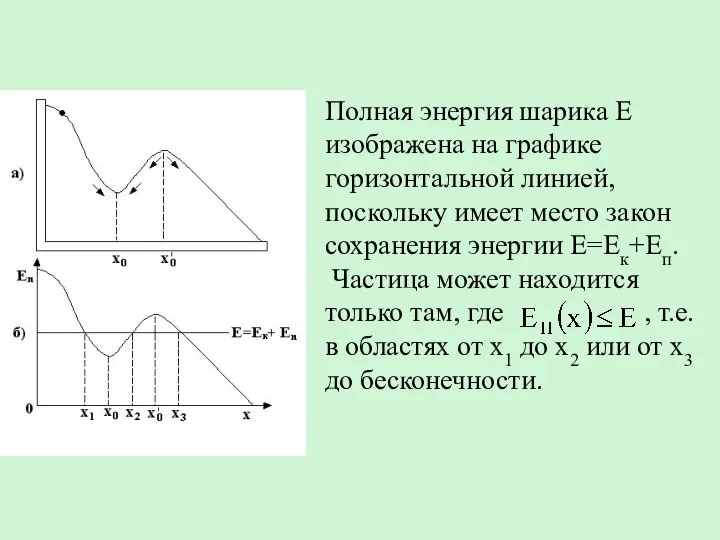
- 29. Полная энергия шарика E изображена на графике горизонтальной линией, поскольку имеет место закон сохранения энергии E=Eк+Eп.
- 30. В области x Таким образом, область x2 называется потенциальной ямой.
- 31. Минимуму потенциальной энергии соответствует на графике точка с координатой x0. Условие минимума потенциальной энергии имеет вид
- 33. Скачать презентацию



























 Метрология. Измерение электрической мощности. Точность измерений
Метрология. Измерение электрической мощности. Точность измерений Электрический ток и его применение
Электрический ток и его применение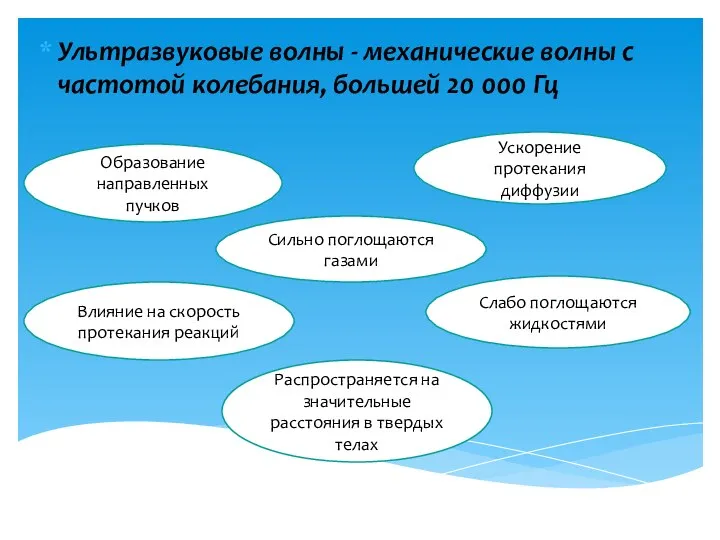 Ультразвуковые волны
Ультразвуковые волны 11_ ОТС_ Модуляция и демодуляция 14
11_ ОТС_ Модуляция и демодуляция 14 Физика колебаний. Лекция 3
Физика колебаний. Лекция 3 Светофор. Внеклассное мероприятие по физике
Светофор. Внеклассное мероприятие по физике Интерференция света
Интерференция света Презентация на тему Равнодействующие силы. Сила трения
Презентация на тему Равнодействующие силы. Сила трения  АЭС_1663630896
АЭС_1663630896 Вес тела. Единицы силы. Связь между силой тяжести и массой тела
Вес тела. Единицы силы. Связь между силой тяжести и массой тела Между двумя точечными заряженными телами сила электрического взаимодействия
Между двумя точечными заряженными телами сила электрического взаимодействия Статистическая радиотехника. Узкополосный случайный процесс
Статистическая радиотехника. Узкополосный случайный процесс Обозначение трехвинтовых насосов
Обозначение трехвинтовых насосов Презентация на тему Величины, характеризующие колебательные движения
Презентация на тему Величины, характеризующие колебательные движения  Единицы напряжения
Единицы напряжения Динамометр в домашних условиях и его применение
Динамометр в домашних условиях и его применение Вещества в электрическом поле
Вещества в электрическом поле Силы в природе
Силы в природе Альтернативные источники энергии
Альтернативные источники энергии Электромагнитная индукция
Электромагнитная индукция Закон сохранения импульса
Закон сохранения импульса Физика твердой Земли. Геотермия
Физика твердой Земли. Геотермия сила упр
сила упр Проводники и диэлектрики в электростатическом поле
Проводники и диэлектрики в электростатическом поле Применение радиоактивных изотопов
Применение радиоактивных изотопов Антенно-фидерные устройства, типы и классификация антенн
Антенно-фидерные устройства, типы и классификация антенн Лабораторная работа. Изучение устройства и принципа работы термодымовой камеры КТД-100
Лабораторная работа. Изучение устройства и принципа работы термодымовой камеры КТД-100 Лейденская банка. Опыт
Лейденская банка. Опыт