Содержание
- 2. Основные понятия статики Совокупность сил, приложенных к какой-либо механической системе, называется системой сил. Две равные по
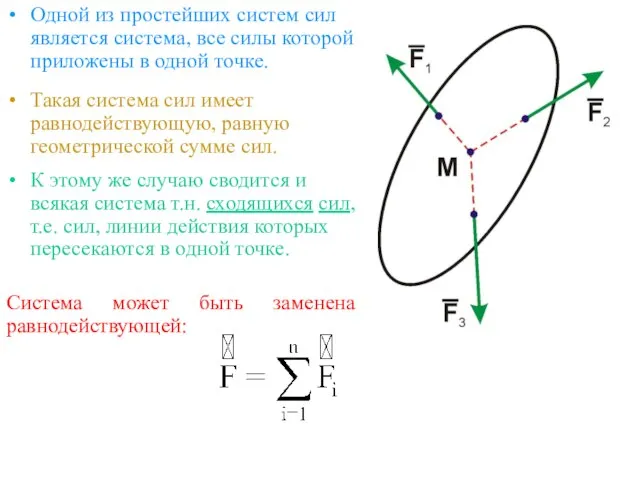
- 3. Одной из простейших систем сил является система, все силы которой приложены в одной точке. Такая система
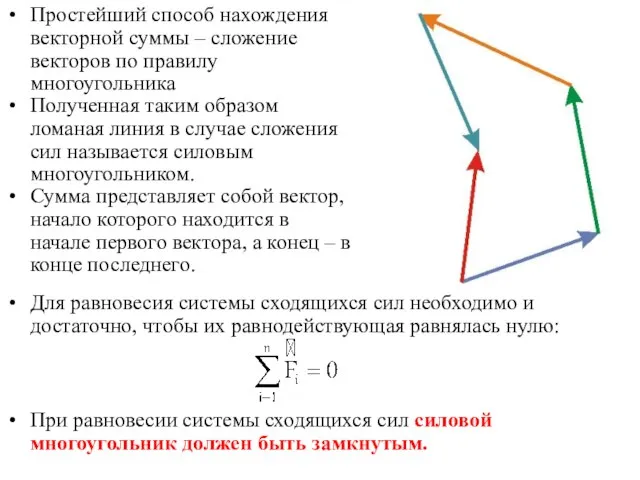
- 4. Простейший способ нахождения векторной суммы – сложение векторов по правилу многоугольника Полученная таким образом ломаная линия
- 5. В проекциях на оси координат условие равновесия дает три уравнения равновесия: Если сходящиеся силы расположены в
- 6. Для решения задач крайне полезной оказывается теорема о трех силах: Если под действием трех сил, лежащих
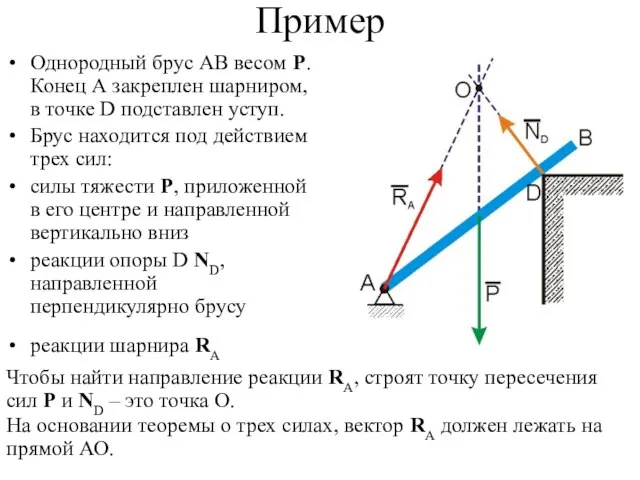
- 7. Пример Однородный брус АВ весом Р. Конец А закреплен шарниром, в точке D подставлен уступ. Брус
- 8. Порядок решения задач на равновесие плоской системы сходящихся сил изобразить все силы, действующие на тело, включая
- 9. Примеры решения задач
- 10. Задача №1 Стержни AC и ВС соединены между собой и с вертикальной стеной посредством шарниров. На
- 11. Силы, действующие на шарнир С: сила Р, приложенная в точке С и направленная вертикально вниз, реакция
- 12. После определения направления сил строится силовой треугольник с соблюдением углов между силами. Сначала строится вектор известной
- 13. Из-за значений углов треугольник получился прямоугольным. Поэтому
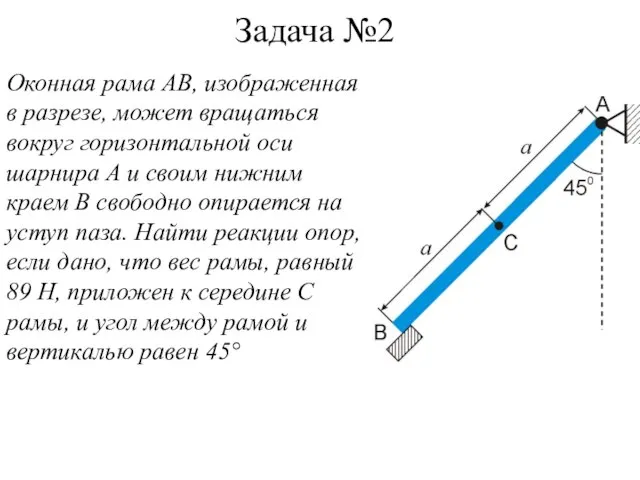
- 14. Задача №2 Оконная рама АВ, изображенная в разрезе, может вращаться вокруг горизонтальной оси шарнира А и
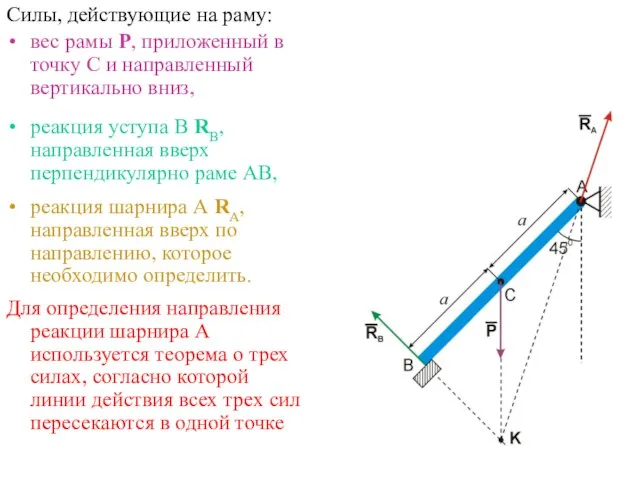
- 15. Силы, действующие на раму: вес рамы Р, приложенный в точку С и направленный вертикально вниз, реакция
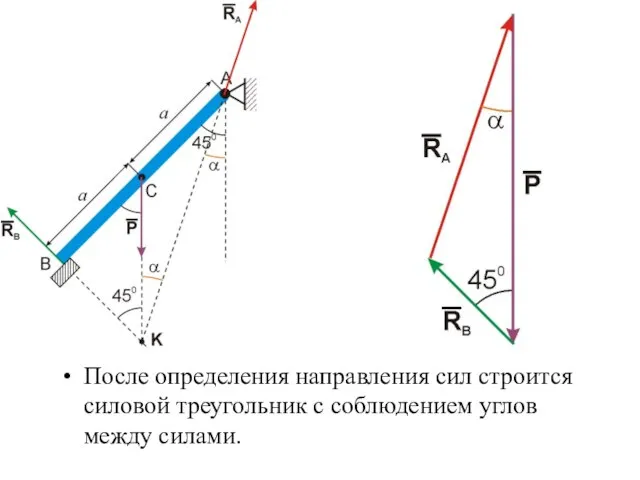
- 16. После определения направления сил строится силовой треугольник с соблюдением углов между силами.
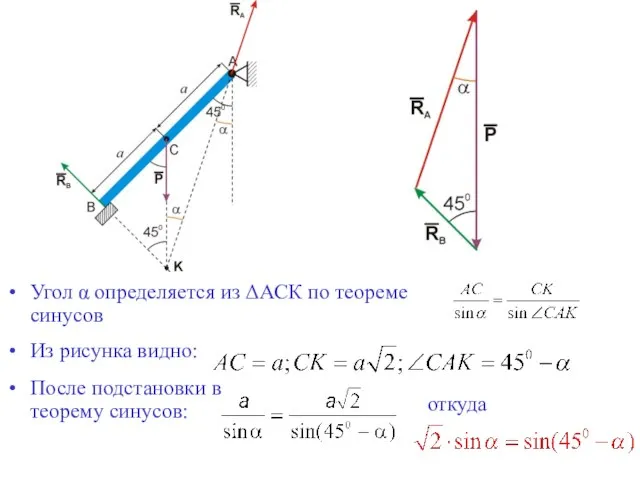
- 17. Угол α определяется из ΔАСК по теореме синусов Из рисунка видно: После подстановки в теорему синусов:
- 18. Решение уравнения
- 19. Применяем теорему синусов к силовому треугольнику: откуда
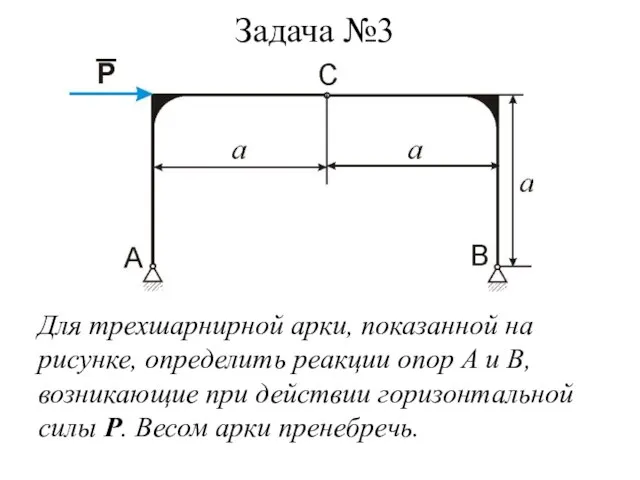
- 20. Задача №3 Для трехшарнирной арки, показанной на рисунке, определить реакции опор А и В, возникающие при
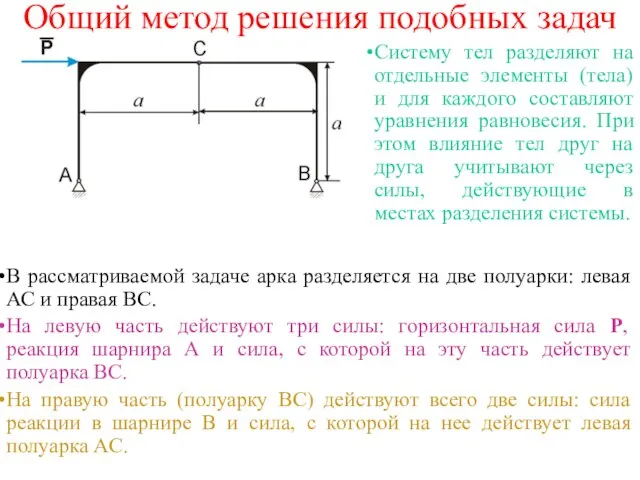
- 21. Общий метод решения подобных задач В рассматриваемой задаче арка разделяется на две полуарки: левая АС и
- 22. На основании первой аксиомы силы,действующие на правую полуарку, должны быть направлены вдоль одной прямой в противоположные
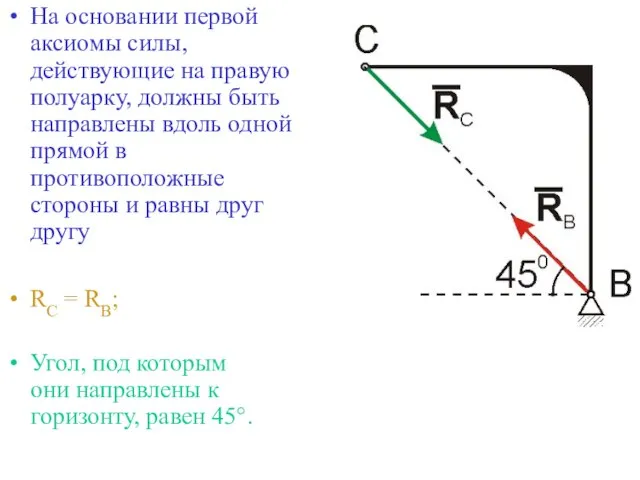
- 23. Силы, действующие на левую полуарку Сила Р Сила со стороны правой полуарки Согласно третьему закону Ньютона,
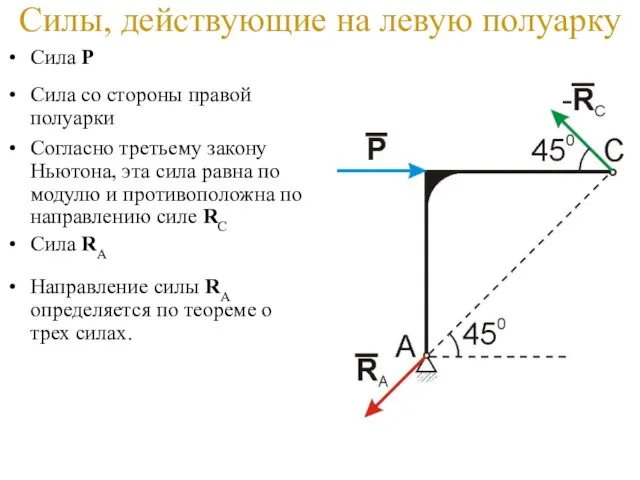
- 25. Скачать презентацию











 Описание физических свойств веществ
Описание физических свойств веществ Презентация по физике "Давление и сила давления" -
Презентация по физике "Давление и сила давления" -  Квантовая теория теплоемкости
Квантовая теория теплоемкости з-н сохр.имп
з-н сохр.имп силы
силы Презентация 3
Презентация 3 7 БШО 1 к - зубч передачи
7 БШО 1 к - зубч передачи Гидравлика машин
Гидравлика машин Презентация на тему Интерференция. Дифракция
Презентация на тему Интерференция. Дифракция  Умная колонка на уроках физики
Умная колонка на уроках физики Пара сил и момент силы относительно точки
Пара сил и момент силы относительно точки Применение явления электромагнитной индукции
Применение явления электромагнитной индукции Инжекторный ДВС
Инжекторный ДВС Нагревание и охлаждение воздуха
Нагревание и охлаждение воздуха Импульс. Закон сохранения импульса
Импульс. Закон сохранения импульса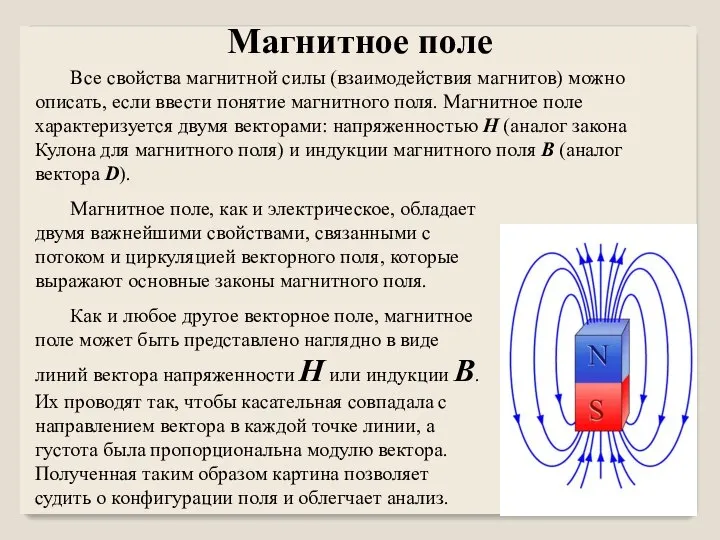 Магнитное поле
Магнитное поле Кроссворд
Кроссворд Силы в природе. 10 класс
Силы в природе. 10 класс Производная функции одной переменной
Производная функции одной переменной Теплотехнология. Приемники энергии
Теплотехнология. Приемники энергии Электромагнитные волны
Электромагнитные волны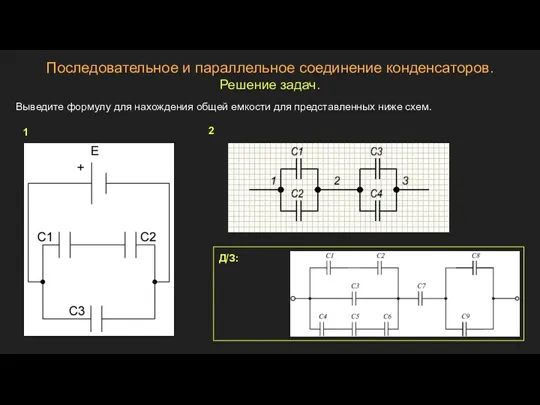 Последовательное и параллельное соединение конденсаторов. Решение задач
Последовательное и параллельное соединение конденсаторов. Решение задач Исследование радиального профиля параметров активной среды лазеров с разрядом в полом катоде
Исследование радиального профиля параметров активной среды лазеров с разрядом в полом катоде Ток в электролитах
Ток в электролитах Линейные звенья первого порядка. Пропорциональные звенья
Линейные звенья первого порядка. Пропорциональные звенья Баллистика. Повторение. Равномерное движение
Баллистика. Повторение. Равномерное движение Источники света
Источники света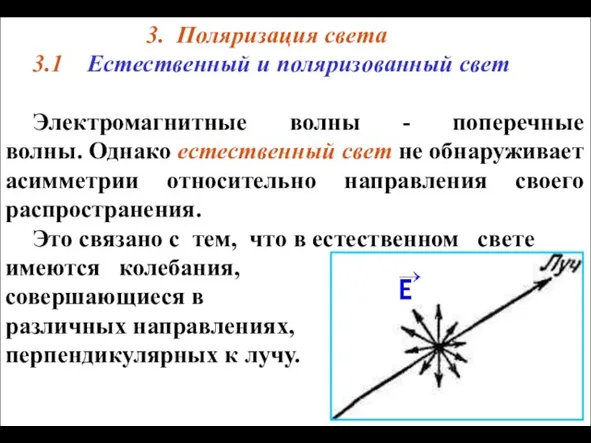 Поляризация света
Поляризация света