Соединение резисторов звездой и треугольником. Расчёт цепей с помощью электрического потенциала

Если имеется три сопротивления, образующих три узла, то такие сопротивления составляют пассивный треугольник (рис. 1, а), а если имеется только один узел — то пассивную звезду (рис. 1,б). Слово "пассивный" означает, что внутри данной цепи отсутствуют какие-либо источники электрической энергии.
Обозначим сопротивления в цепи треугольника — большими (прописными) буквами (RAB, RBD, RDA), а в цепи звезды — малыми (ra, rb, rd).
Преобразование треугольника в звезду
Схему пассивного треугольника сопротивлений можно заменить эквивалентной схемой пассивной звезды, при этом все токи в ветвях, не подвергавшихся преобразованию (т. е. все, что на рис. 1, а и 1, б находится за пределами штриховой кривой), остаются без всяких изменений.
Например, если к узлам А, В, D в схеме треугольника притекали (или утекали) токи IА, IB, и ID, то и в схеме эквивалентной звезды к точкам А, В, D будут притекать (или утекать) те же самые токи IА, IB, и ID.
Рис. 1 Схемы соединения звездой и треугольником

Расчет сопротивлений в схеме звезды ra, rb, rd по известным сопротивлениям треугольника производятся по формулам
Данные выражения образуются по следующим правилам. Знаменатели у всех выражений одинаковые и представляют сумму сопротивлений треугольника, каждый числитель является произведением тех сопротивлений, которые в схеме треугольника примыкают к точке, к которой примыкают сопротивления звезды, определяемые в данном выражении.
Например, сопротивление гА в схеме звезды примыкает к точке А (см. рис. 1, б). Следовательно, в числителе следует написать произведение сопротивлений RAB и RDA, поскольку в схеме треугольника эти сопротивления примыкают к этой же точке А и т. д. Если известны сопротивления звезды ra, rb, rd, то можно рассчитать сопротивления эквивалентного треугольника RAB, RBD, RDA по формулам:

Из приведенных формул видно, что числители всех выражений одинаковые и представляют парные сочетания сопротивлений звезды, а в знаменателе записывается сопротивление, примыкающее к той точке звезды, к которой не примыкает искомое сопротивление треугольника.
Например, следует определить R1, т. е. сопротивление, примыкающее в схеме треугольника к точкам А и В, следовательно, в знаменателе должно быть сопротивление гэ = rd, поскольку это сопротивление в схеме звезды не примыкает ни к точке А, ни к точке В и т. д.
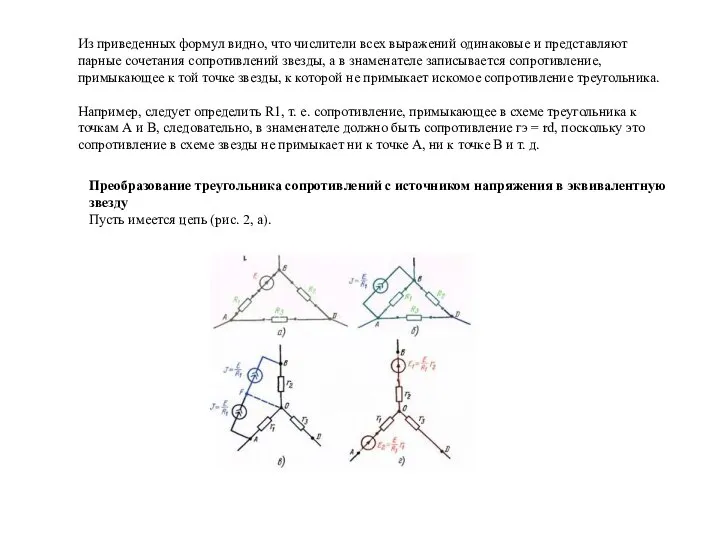
Преобразование треугольника сопротивлений с источником напряжения в эквивалентную звезду
Пусть имеется цепь (рис. 2, а).

Рис. 2. Преобразование треугольника сопротивлений с источником напряжения в эквивалентную звезду
Требуется преобразовать данный треугольник в звезду. Если бы в схеме не было источника Е, то преобразование можно было произвести с помощью формул преобразования пассивного треугольника в пассивную звезду. Однако данные формулы справедливы только для пассивных цепей, поэтому в цепях с источниками необходимо проделать ряд преобразований.
Заменим источник напряжения Е эквивалентным источником тока, цепь рис. 2, а приобретает вид рис. 2, б. В результате преобразования получился пассивный треугольник R1, R2, R3, который можно превратить в эквивалентную пассивную звезду, причем между точками АВ остается неизменнным источник J = E/Rt.
Расщепим источник J и соединим точку F с точкой 0 (на рис. 2, в показано штриховой линией). Теперь источники тока можно заменить эквивалентными источниками напряжения, при этом получается схема эквивалентной звезды с источниками напряжения (рис. 2, г).
Потенциальной диаграммой называется графическое изображение распределения электрического потенциала вдоль замкнутого контура в зависимости от сопротивления участков, входящих в выбранный контур.

Потенциальной диаграммой называется графическое изображение распределения электрического потенциала вдоль замкнутого контура в зависимости от сопротивления участков, входящих в выбранный контур.
Для построения потенциальной диаграммы выбирают замкнутый контур. Этот контур разбивают на участки таким образом, чтобы на участке находился один потребитель или источник энергии. Пограничные точки между участками необходимо обозначить буквами или цифрами.
Произвольно заземляют одну точку контура, её потенциал условно считается нулевым. Обходя контур по часовой стрелке от точки с нулевым потенциалом, определяют потенциал каждой последующей пограничной точки как алгебраической суммы потенциала предыдущей точки и изменения потенциала между этими соседними точками.
Изменение потенциала на участке зависит от состава цепи между точками. Если на участке включен потребитель энергии (резистор), то изменение потенциала численно равно падению напряжения на этом резисторе. Знак этого изменения определяют направлением тока. При совпадении направлений тока и обхода контура знак отрицательный, в противном случае он положительный.
Если на участке находится источник ЭДС, то изменение потенциала здесь численно равно величине ЭДС данного источника. При совпадении направления обхода контура и направления ЭДС изменение потенциала положительно, в противном случае оно отрицательно.
После расчета потенциалов всех точек строят в прямоугольной системе координат потенциальную диаграмму. На оси абсцисс откладывают в масштабе сопротивление участков в той последовательности, в которой они встречались при обходе контура, а по оси ординат – потенциалы соответствующих точек. Потенциальная диаграмма начинается с нулевого потенциала и заканчивается после обхода контура таковым.

Построение потенциальной диаграммы электрической цепи
В данном примере потенциальную диаграмму строим для первого контура цепи, схема которой изображена на рисунке 1.
Рис. 1. Схема сложной электрической цепи
В рассматриваемый контур входят два источника питания E1 и E2, а также два потребителя энергии r1, r2.
Разбиваем данный контур на участки, границы которых обозначаем буквами a, b, c, d. Заземляем точку а, условно считая её потенциал нулевым, и обходим контур по часовой стрелке от этой точки. Таким образом, φa = 0.

Следующей точкой на пути обхода контура будет точка b. На участке ab находится источник ЭДС Е1. Так как на данном участке мы идем от отрицательного полюса источника к положительному, то потенциал повышается на величину Е1:
φb = φa + E1 = 0 + 24 = 24 В
При переходе от точки b к точке c происходит уменьшение потенциала на величину падения напряжения на резисторе r1 (направление обхода контура совпадает с направлением тока в резисторе r1):
φс = φb - I1r1 = 24 - 3 х 4 = 12 В
При переходе к точке d потенциал возрастает на величину падения напряжения на резисторе r2 (на этом участке направление тока встречно направлению обхода контура):
φd = φc + I2r2 = 12 + 0 х 4 = 12 В
Потенциал точки а меньше потенциала точки d на величину ЭДС источника E2 (направление ЭДС встречно направлению обхода контура):
φa = φd - E2 = 12 - 12 = 0
Результаты расчета используют для построения потенциальной диаграммы. На оси абсцисс откладывают сопротивление участков в той последовательности, как они встречаются при обходе контура от точки с нулевым потенциалом. Вдоль оси ординат откладывают рассчитанные ранее потенциалы соответствующих точек (рисунок 2).