Содержание
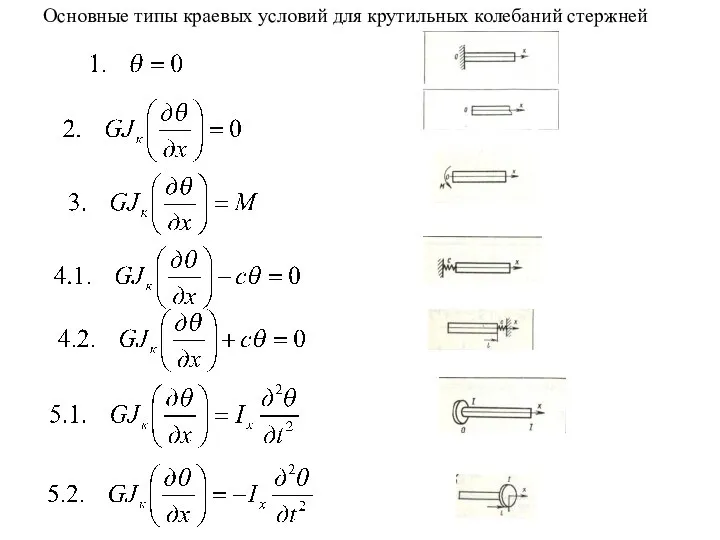
- 2. Основные типы краевых условий для крутильных колебаний стержней
- 3. В технической теории крутильные колебания стержня описывают уравнением при м = 0 Если стержень имеет постоянные
- 4. Общее решение. Для стержня, совершающего собственные крутильные колебания, переменные разделяют введением временного множителя, гармонически изменяющегося со
- 7. Скачать презентацию



 Шлифовальные станки
Шлифовальные станки Макроскопическая намагниченность, прецессия
Макроскопическая намагниченность, прецессия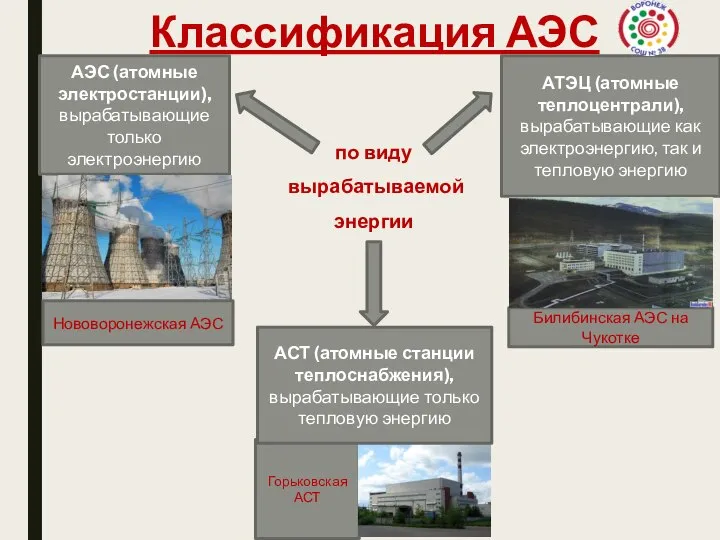 Классификация АЭС
Классификация АЭС Презентация на тему Амперметр
Презентация на тему Амперметр  Броуновское движение. Диффузия. Силы взаимодействия молекул
Броуновское движение. Диффузия. Силы взаимодействия молекул Күн элементтерінің эффективтігінің проблемасы
Күн элементтерінің эффективтігінің проблемасы Механические волны
Механические волны Магнитостатическое поле в вакууме. Часть 3
Магнитостатическое поле в вакууме. Часть 3 Занимательные опыты для детей
Занимательные опыты для детей Презентация-повторение курса физики 8 класса
Презентация-повторение курса физики 8 класса Задачи по физике. Электрический ток
Задачи по физике. Электрический ток Метод проектов на уроках физики
Метод проектов на уроках физики PITSTOP_05 Project Summary
PITSTOP_05 Project Summary Дирижаблестроение. Тема № 1
Дирижаблестроение. Тема № 1 Разметчик Фибоначчи
Разметчик Фибоначчи Использование электромагнитной индукции
Использование электромагнитной индукции Двигатель Внутреннего Сгорания
Двигатель Внутреннего Сгорания Анализ видов и кинематических параметров движений
Анализ видов и кинематических параметров движений Разработка конструкции микрореакторной установки для получения водорода из водно-спиртовой смесиПрезентация
Разработка конструкции микрореакторной установки для получения водорода из водно-спиртовой смесиПрезентация Указатель уровня топлива
Указатель уровня топлива Приёмосдаточные испытания схемы электропроводки жилого помещения
Приёмосдаточные испытания схемы электропроводки жилого помещения Принципы действия различных типов двигателей. Двигатели внешнего сгорания
Принципы действия различных типов двигателей. Двигатели внешнего сгорания Исследование схемы измерения сопротивления заземлителя МС-08
Исследование схемы измерения сопротивления заземлителя МС-08 实验五 功率放大电路
实验五 功率放大电路 Амперметр. Измерение силы тока
Амперметр. Измерение силы тока Закон Джоуля-Ленца
Закон Джоуля-Ленца Первоначальные сведения о строении вещества
Первоначальные сведения о строении вещества Б1. В 16. Типаж технологического оборудования. Практическое занятие № 2. Методы и средства диагностирования
Б1. В 16. Типаж технологического оборудования. Практическое занятие № 2. Методы и средства диагностирования