Содержание
- 2. Темы для СРС: Пружинный маятник. Затухающие колебания. Характеристики затухающих колебаний. Вынужденные колебания. Амплитуда и фаза колебаний.
- 3. 1. Колебания. Основные понятия Периодическим колебанием называется процесс, при котором система (например, механическая) возвращается в одно
- 4. 1.1 Гармонические колебания
- 5. 1.1 Гармонические колебания
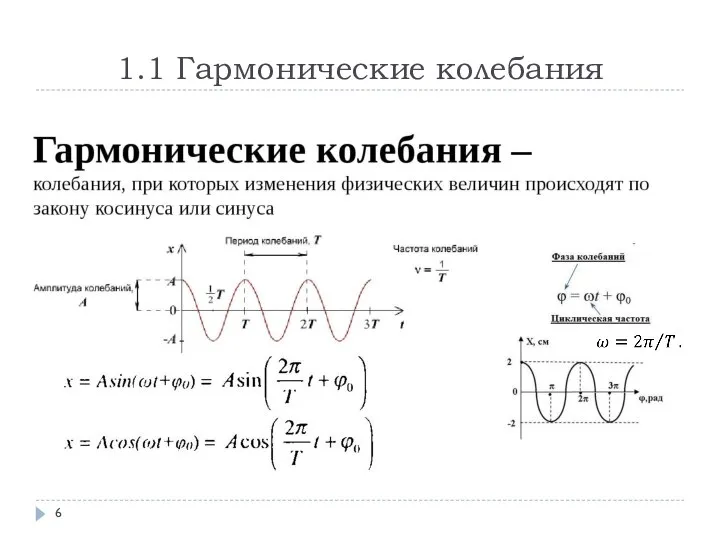
- 6. 1.1 Гармонические колебания
- 7. 1.2 Скорость и ускорение колебаний
- 8. 1.3 Математический маятник.
- 9. 1.3 Вывод закона движения математического маятника
- 10. 1.4. Физический маятник Физический маятник - твердое тело, закрепленное на неподвижной горизонтальной оси (оси подвеса), не
- 11. 1.4 Вывод закона движения физического маятника
- 12. Определение. Центр качения – математическая точка, в которой можно сосредоточить всю массу физического маятника, при этом
- 13. 2.1 Пружинный маятник. Затухающие колебания
- 14. 2.1 Дифференциальное уравнение свободных затухающих колебаний линейной системы задается в виде: (1) где s – колеблющаяся
- 15. 2.2 Характеристики затухающих колебаний Время релаксации – Промежуток времени , в течение которого амплитуда затухающих колебаний
- 16. 2.3 Пример (пружинный маятник) Для пружинного маятника массой т, совершающего малые колебания под действием упругой силы
- 17. 3.1 Вынужденные колебания Чтобы в реальной механической колебательной системе полу- чить незатухающие колебания, надо компенсировать потери
- 18. 3.1 Вынужденные колебания
- 19. 3.1 Вынужденные колебания Это комплексное число удобно представить в экспоненциальной форме: где (3) и (4) Следовательно,
- 20. 3.2 Амплитуда и фаза вынужденных колебаний. Рассмотрим зависимость амплитуды А вынужденных колебаний от частоты Из следует,
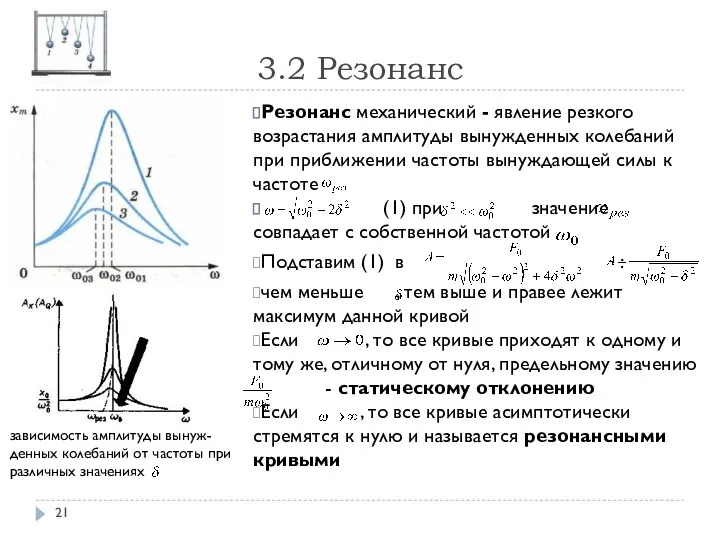
- 21. 3.2 Резонанс Резонанс механический - явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы
- 22. 3.2 Резонанс. Амплитуда скорости Из вытекает, что при малом затухании резонансная амплитуда смещения где Q –
- 23. 3.2 Резонанс. Зависимость φ от ω при разных коэффициентах δ при изменении ω изменяется и сдвиг
- 24. 3.3 Применение резонанса. Явления резонанса могут быть как вредными, так и полезными При конструировании машин и
- 25. 3.3 Применение резонанса. Явления резонанса могут приводить к серьезным разрушениям. Так в 1940г в США висячий
- 26. 3.3 Применение резонанса.
- 28. Скачать презентацию























 0008959c-88e65e04
0008959c-88e65e04 Презентация на тему Калейдоскоп физических явлений
Презентация на тему Калейдоскоп физических явлений  Ускорение. Движение с постоянным ускорением. Уравнение движения. (10 класс)
Ускорение. Движение с постоянным ускорением. Уравнение движения. (10 класс) Сила упругости
Сила упругости Классификация томографов и магнитов
Классификация томографов и магнитов Проблемы применения нанотехнологии
Проблемы применения нанотехнологии Презентация на тему Импульс Закон сохранения импульса
Презентация на тему Импульс Закон сохранения импульса  Электрический ток в металлах
Электрический ток в металлах Презентация на тему Принцип относительности в механике. Постулаты теории относительности (11 класс)
Презентация на тему Принцип относительности в механике. Постулаты теории относительности (11 класс)  Христиан Гюйгенс вклад в развитие механики
Христиан Гюйгенс вклад в развитие механики Простые механизмы. Рычаг. Правило равновесия рычага
Простые механизмы. Рычаг. Правило равновесия рычага Электрические машины. Законы электромеханики
Электрические машины. Законы электромеханики Электромагнетизм
Электромагнетизм Газораспределительный механизм
Газораспределительный механизм Магнитное поле Земли
Магнитное поле Земли Работа, мощность силы. Кинетическая энергия. Лекция 9
Работа, мощность силы. Кинетическая энергия. Лекция 9 Электрические колебания. Колебательный контур. Превращение энергии при электромагнитных колебаниях
Электрические колебания. Колебательный контур. Превращение энергии при электромагнитных колебаниях Закон Ома для участка электрической цепи
Закон Ома для участка электрической цепи Разработка и моделирование МЭМС-датчика давления воздушной среды
Разработка и моделирование МЭМС-датчика давления воздушной среды Периодическое движение
Периодическое движение Червячные передачи
Червячные передачи Теория линейных электрических цепей
Теория линейных электрических цепей Исследование зависимостей термодинамических величин
Исследование зависимостей термодинамических величин Транзисторы. Практическое применение транзисторов, диодов и конденсаторов. Лекция 6
Транзисторы. Практическое применение транзисторов, диодов и конденсаторов. Лекция 6 Поршневые компрессоры
Поршневые компрессоры Гуманитарная направленность преподавания физики при организации самостоятельной работы студентов
Гуманитарная направленность преподавания физики при организации самостоятельной работы студентов Вопросы для аттестации. Квантовая теория
Вопросы для аттестации. Квантовая теория Презентация на тему Атом
Презентация на тему Атом