Содержание
- 2. Одним из таких методов является метод расчета переходных процессов, основанный на преобразовании Лапласа, который назван операторным.
- 3. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА Будем под р понимать комплексное число p = a + jb, (2.28) где а
- 4. Знак «≓» называют знаком соответствия. Верхний предел интеграла (2.29) равен бесконечности. Интегралы с бесконечным верхним пределом
- 5. Определим изображения некоторых простейших функций. Изображение постоянной Найдем изображение функции f(t) = A, где А —постоянная
- 6. Изображение показательной функции еαt Вместо f(t) подставим в (2.29) еαt: Таким образом, eαt ≓ 1/(p –
- 7. Формула (2.33) позволяет найти изображение комплекса синусоидального тока: С этой целью обе части (2.33) умножим на
- 8. Изображение производных Пусть функции f(t) соответствует изображение F(p). Требуется найти изображение первой производной df(t)/dt, если известно,
- 9. поскольку а Поэтому df(t)/dt ≓pF(p) – f(0). (2.38) Повторным применением операции, выражаемой формулой (2.38), можно распространить
- 10. Если, в частности, f(0) = f/(0) = ... = f(n-1)(0) = 0, то и, следовательно, n-кратному
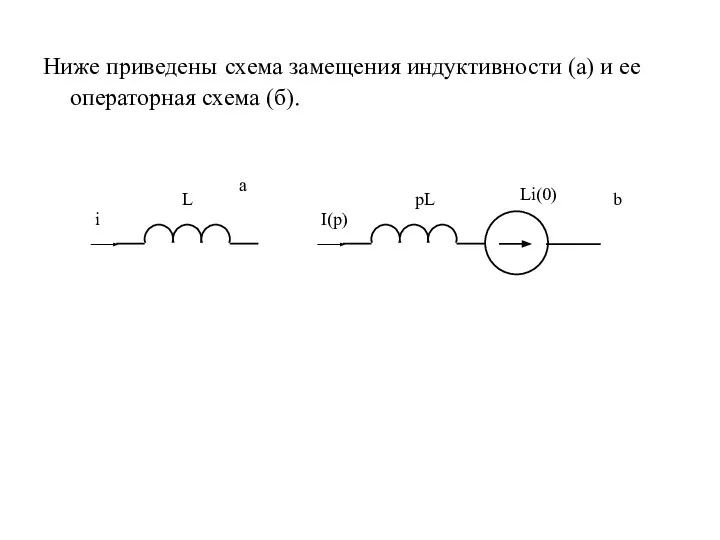
- 11. Ниже приведены схема замещения индуктивности (а) и ее операторная схема (б). Li(0) b pL a
- 12. Изображение интегралов Требуется найти изображение функции если известно, что функции f(t) соответствует изображение F(p). Подвергнем функцию
- 13. Первое слагаемое правой части при подстановке и верхнего и нижнего пределов обращается в нуль. При подстановке
- 14. Тогда, найдя в соответствии с (2.40) изображение интеграла тока и учтя, что изображение начального напряжения uC(0)
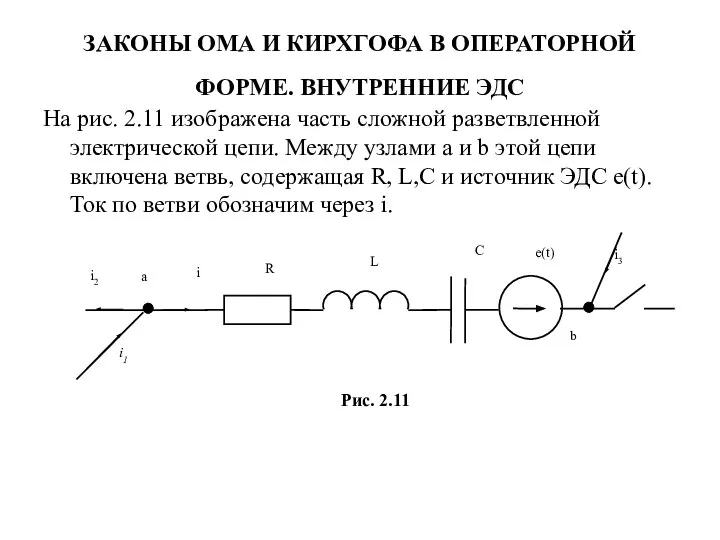
- 15. ЗАКОНЫ ОМА И КИРХГОФА В ОПЕРАТОРНОЙ ФОРМЕ. ВНУТРЕННИЕ ЭДС На рис. 2.11 изображена часть сложной разветвленной
- 16. Замыкание ключа приводит к переходному процессу в схеме. Пусть до коммутации ток i = i(0–) и
- 17. Каждое из слагаемых уравнения (2.50) заменим его операторным изображением: (2.51) где – операторное сопротивление участка цепи
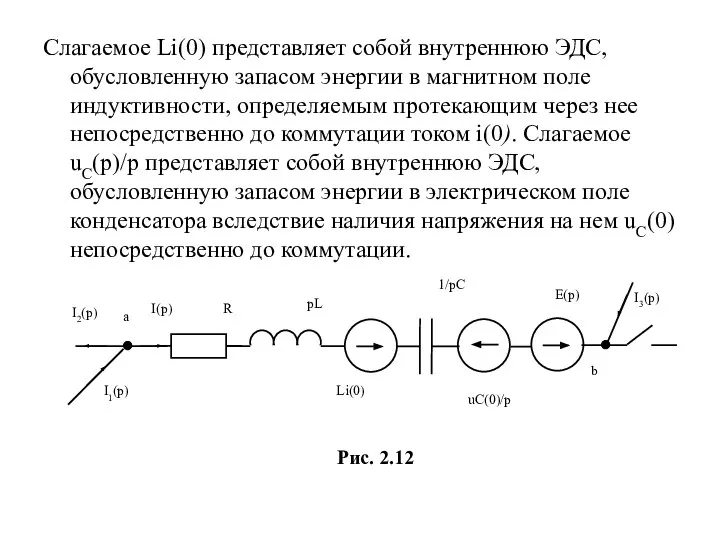
- 18. Слагаемое Li(0) представляет собой внутреннюю ЭДС, обусловленную запасом энергии в магнитном поле индуктивности, определяемым протекающим через
- 19. ПЕРВЫЙ ЗАКОН КИРХГОФА В ОПЕРАТОРНОЙ ФОРМЕ По первому закону Кирхгофа, алгебраическая сумма мгновенных значений токов, сходящихся
- 20. В общем случае (2.55) Уравнение (2.55) является записью первого закона Кирхгофа в операторной форме.
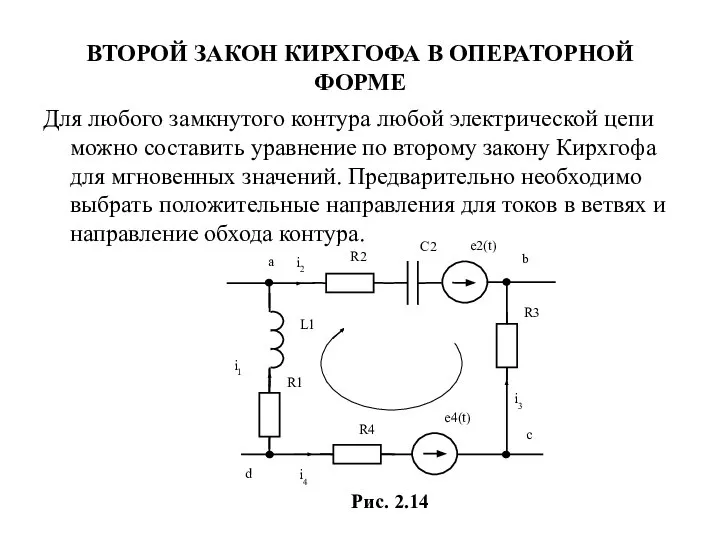
- 21. ВТОРОЙ ЗАКОН КИРХГОФА В OПEРАТОРНОЙ ФОРМЕ Для любого замкнутого контура любой электрической цепи можно составить уравнение
- 22. Запишем для контура рис. 2.14 уравнение по второму закону Kирхгофа при его обходе по часовой стрелке.
- 23. где Это уравнение, записанное в более общем виде, (2.56) представляет собой математическую запись второго закона Кирхгофа
- 24. СОСТАВЛЕНИЕ УРАВНЕНИЙ ДЛЯ ИЗОБРАЖЕНИЙ Уравнения для изображений по форме аналогичны уравнениям, составленным для той же цепи
- 25. ПЕРЕХОД ОТ ИЗОБРАЖЕНИЙ К ФУНКЦИИ ВРЕМЕНИ Вторым этапом операторного метода расчета переходных процессов является обратный переход
- 26. В общем случае изображение тока или напряжения всегда приводится к виду . Студентам рекомендуется использовать так
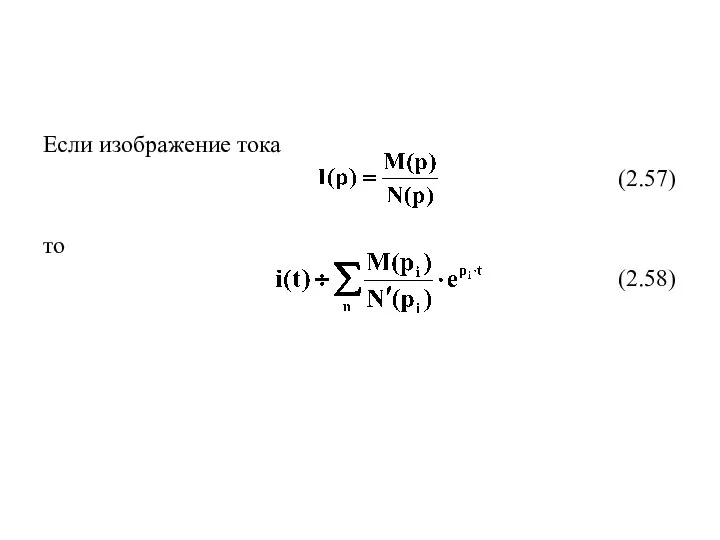
- 27. Если изображение тока (2.57) то (2.58)
- 29. Скачать презентацию





















 Основные понятия механики
Основные понятия механики Основы МКТ идеального газа. Тренировочный тест
Основы МКТ идеального газа. Тренировочный тест Osnovy_AU
Osnovy_AU Презентация по физике "Расчет стоимости электроэнергии. Электроприборы в быту. Техника электробезопасности" -
Презентация по физике "Расчет стоимости электроэнергии. Электроприборы в быту. Техника электробезопасности" -  Система. Объекты
Система. Объекты Физика конденсированного состояния (лекции 11 - 14)
Физика конденсированного состояния (лекции 11 - 14) Гидроудар. Изэнтропические соотношения в сжимаемых средах. Уравнение баланса. Число Маха и скоростной коэффициент
Гидроудар. Изэнтропические соотношения в сжимаемых средах. Уравнение баланса. Число Маха и скоростной коэффициент Сверхпроводниковые материалы
Сверхпроводниковые материалы Обслуживание тормозной системы
Обслуживание тормозной системы Импульс. Закон сохранения импульса
Импульс. Закон сохранения импульса Разработка технологического процесса ТО и ремонта ходовой части автомобиля КамАЗ 5320 с применением газовой резки
Разработка технологического процесса ТО и ремонта ходовой части автомобиля КамАЗ 5320 с применением газовой резки Плавание судов
Плавание судов Закон всемирного тяготения
Закон всемирного тяготения Исследование полей Токов смещения
Исследование полей Токов смещения Отражение звука, эхо. Решение задач
Отражение звука, эхо. Решение задач График гармонического колебания
График гармонического колебания Самостоятельная работа 66 урок
Самостоятельная работа 66 урок Исследование оптических свойств халькогенидных стеклообразных полупроводников
Исследование оптических свойств халькогенидных стеклообразных полупроводников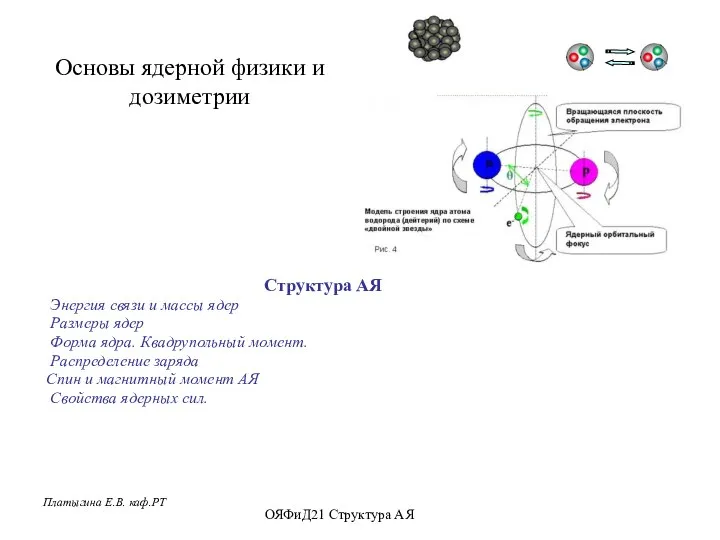 Основы ядерной физики и дозиметрии
Основы ядерной физики и дозиметрии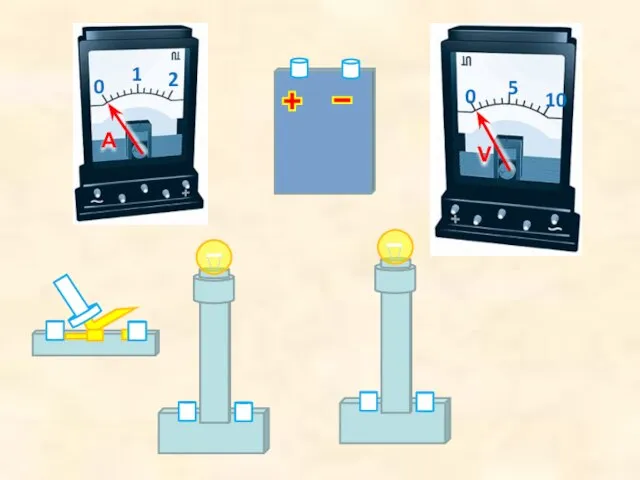 Последовательное соединение проводников. Условное обозначение
Последовательное соединение проводников. Условное обозначение Методы исследование структуры. Часть 1
Методы исследование структуры. Часть 1 Расчёт массы и объёма тела по его плотности. 7 класс
Расчёт массы и объёма тела по его плотности. 7 класс Колебательный контур
Колебательный контур Электронные лампы. Триоды и диоды
Электронные лампы. Триоды и диоды Второе начало термодинамики. Принцип действия тепловой машины и ее КПД. Лекция 6
Второе начало термодинамики. Принцип действия тепловой машины и ее КПД. Лекция 6 Курвиметр. Велокомпьютер с цифровым одометром
Курвиметр. Велокомпьютер с цифровым одометром Физика в ребусах
Физика в ребусах Презентация на тему Теплопроводность
Презентация на тему Теплопроводность