Содержание
- 2. Цель: изучение способов определения центра тяжести твердого тела. План 1. Понятие центра тяжести твердого тела. 2.
- 3. 1. Определение центра тяжести тела
- 4. По закону всемирного тяготения на все частицы тела, находящегося вблизи земной поверхности, действуют силы притяжения их
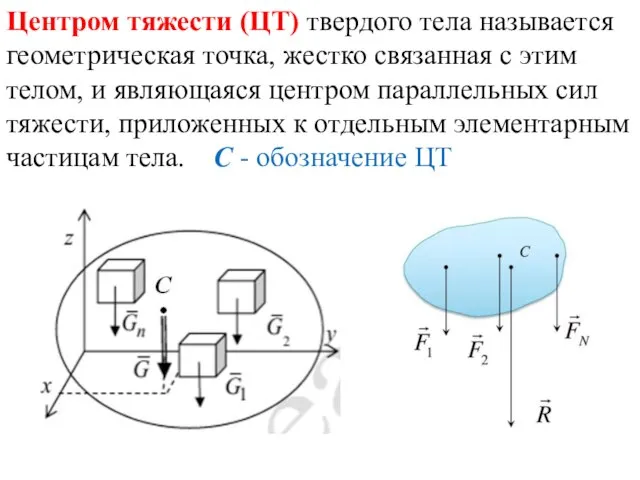
- 5. Центром тяжести (ЦТ) твердого тела называется геометрическая точка, жестко связанная с этим телом, и являющаяся центром
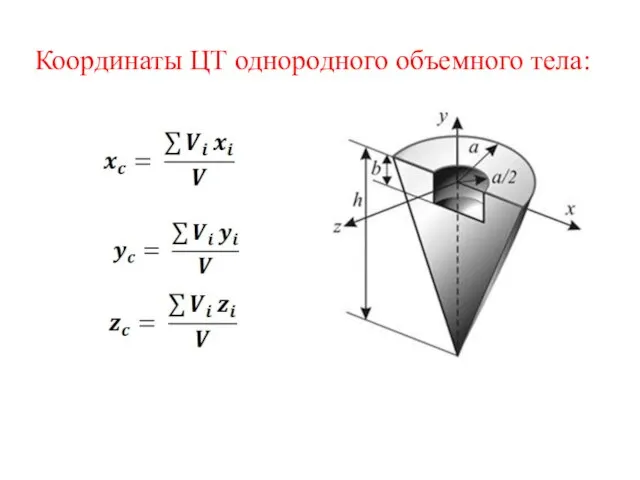
- 6. Координаты ЦТ однородного объемного тела:
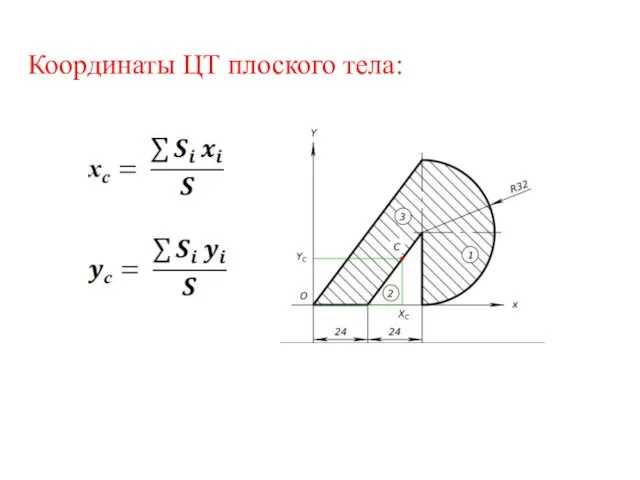
- 7. Координаты ЦТ плоского тела:
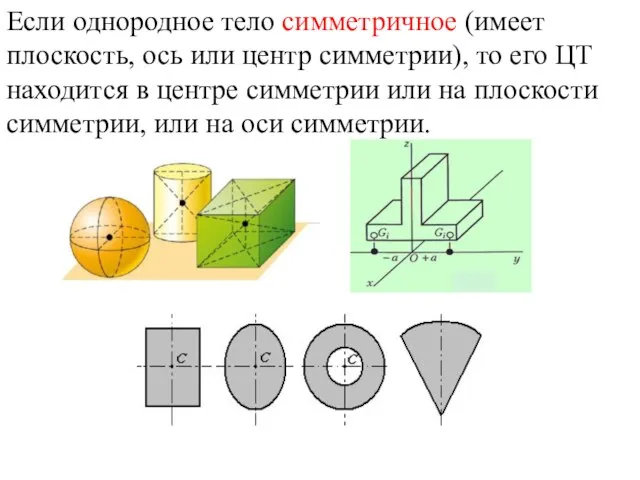
- 8. Если однородное тело симметричное (имеет плоскость, ось или центр симметрии), то его ЦТ находится в центре
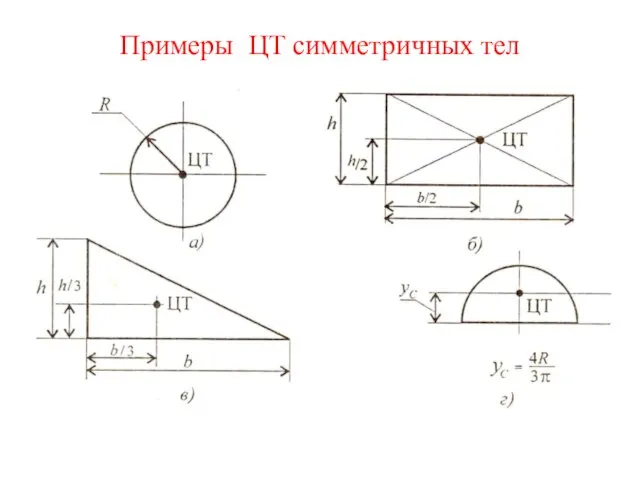
- 9. Примеры ЦТ симметричных тел
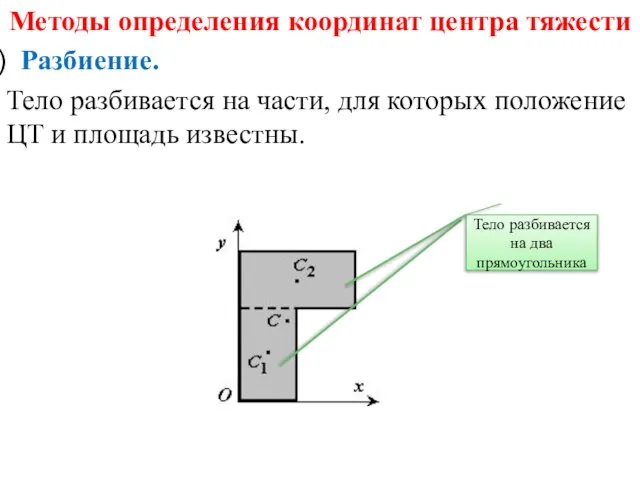
- 10. Методы определения координат центра тяжести Разбиение. Тело разбивается на части, для которых положение ЦТ и площадь
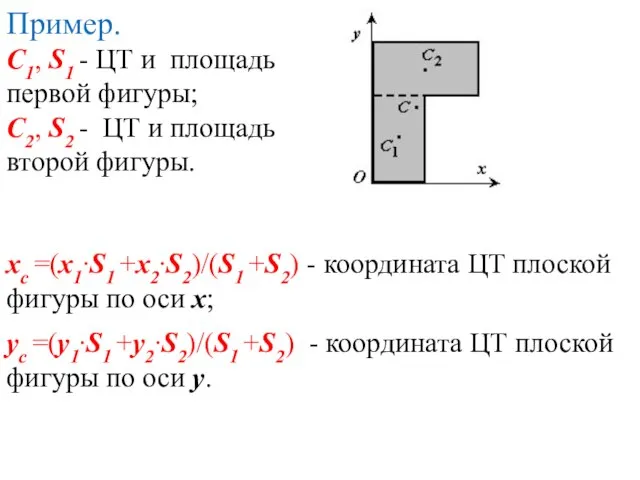
- 11. Пример. С1, S1 - ЦТ и площадь первой фигуры; С2, S2 - ЦТ и площадь второй
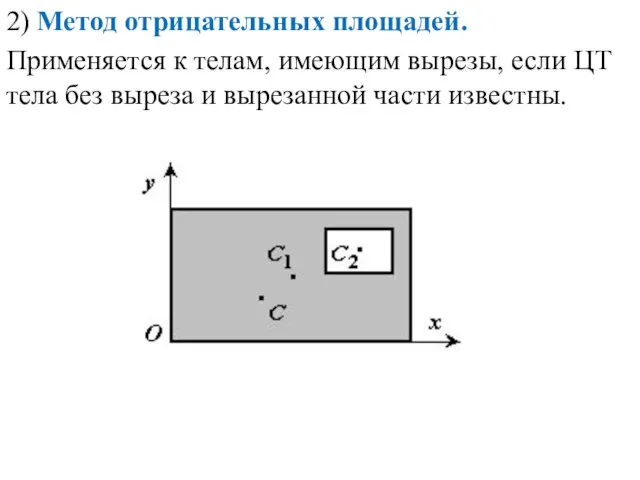
- 12. 2) Метод отрицательных площадей. Применяется к телам, имеющим вырезы, если ЦТ тела без выреза и вырезанной
- 13. Пример. С1, S1 - ЦТ и площадь первой фигуры; С2, S2 - ЦТ и площадь второй
- 14. Пример сложной фигуры, при определении ЦТ которой применяются оба метода
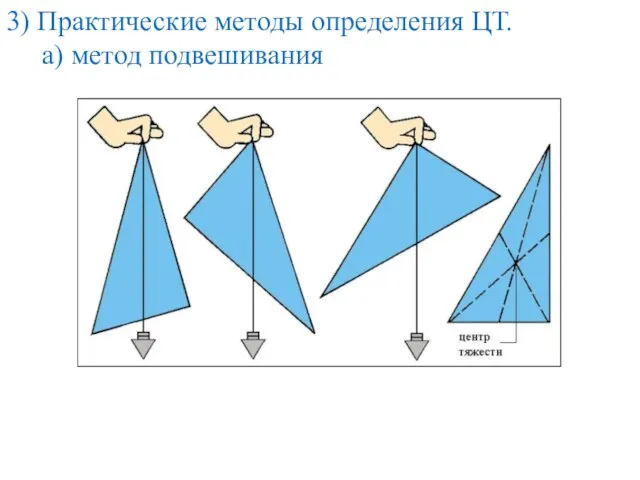
- 15. 3) Практические методы определения ЦТ. а) метод подвешивания
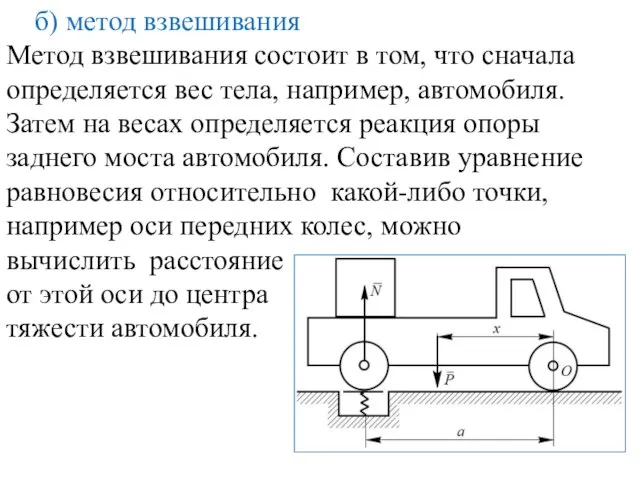
- 16. б) метод взвешивания Метод взвешивания состоит в том, что сначала определяется вес тела, например, автомобиля. Затем
- 17. 2. Примеры расчета координат центра тяжести
- 18. Пример 1. Найти координаты ЦТ плоской фигуры, изображенной на рисунке. Выбираем оси координат так, чтобы нижний
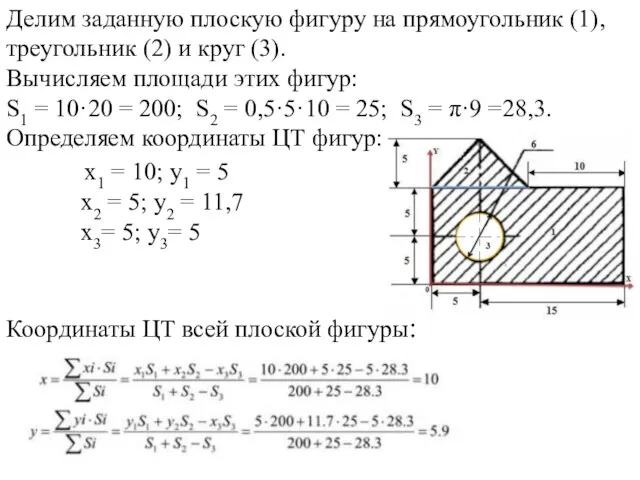
- 19. Делим заданную плоскую фигуру на прямоугольник (1), треугольник (2) и круг (3). Вычисляем площади этих фигур:
- 20. Пример 2. Определить координаты ЦТ составного сечения. Сечение состоит из листа и прокатных профилей (швеллера, двутавра).
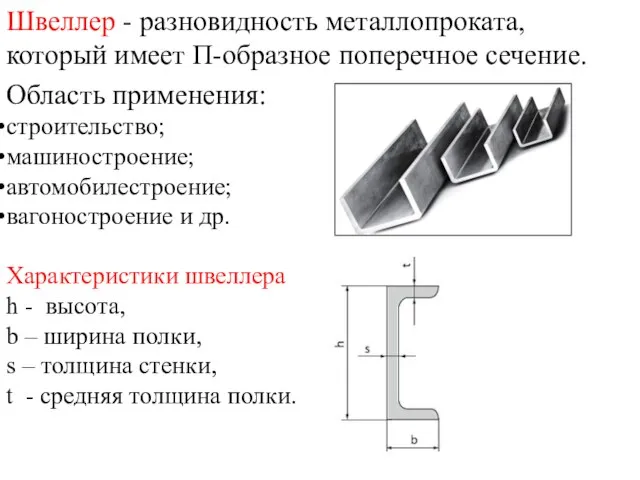
- 21. Швеллер - разновидность металлопроката, который имеет П-образное поперечное сечение. Область применения: строительство; машиностроение; автомобилестроение; вагоностроение и
- 22. Двутавр – балочный профиль из высокопрочной стали с Н-образным поперечным сечением. Двутавровые конструкции хорошо переносят сопротивление
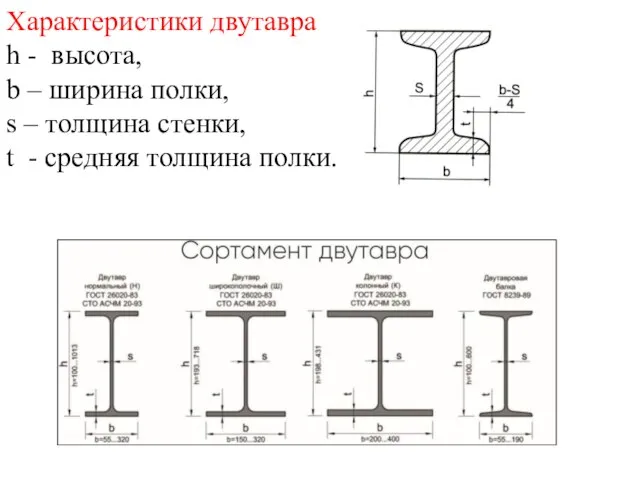
- 23. Характеристики двутавра h - высота, b – ширина полки, s – толщина стенки, t - средняя
- 24. Задача. Сечение состоит из листа, швеллера, двутавра. Обозначаем фигуры номерами и выписываем из таблиц стандартов необходимые
- 25. Координаты центров тяжести каждой фигуры можно определить по чертежу. Составное сечение симметрично, поэтому ЦТ находится на
- 26. Определение центра тяжести составного сечения: Ответ: хС =0 уС = 10 см
- 28. Скачать презентацию












 Презентация
Презентация Простые механизмы
Простые механизмы Условия, при которых тело плавает и при которых тонет
Условия, при которых тело плавает и при которых тонет Электричество. Электрический ток
Электричество. Электрический ток Тонкослойная хроматография
Тонкослойная хроматография Линии влияния усилий в фермах
Линии влияния усилий в фермах Принцип суперпозиции полей
Принцип суперпозиции полей Соединение проводников
Соединение проводников Презентация на тему Применение фотоэффекта
Презентация на тему Применение фотоэффекта  Процессы и аппараты химической технологии
Процессы и аппараты химической технологии Спор Альберта Эйнштейна и Нильса Бора
Спор Альберта Эйнштейна и Нильса Бора Индукция магнитного поля
Индукция магнитного поля Волновые передачи
Волновые передачи лекция 1
лекция 1 Линейные звенья первого порядка. Пропорциональные звенья
Линейные звенья первого порядка. Пропорциональные звенья Практические занятия
Практические занятия Магнитное поле
Магнитное поле Закон Ома для участка цепи. Сопротивление
Закон Ома для участка цепи. Сопротивление Закон всемирного тяготения
Закон всемирного тяготения Презентация на тему Электромагнитная индукция. Опыты Фарадея
Презентация на тему Электромагнитная индукция. Опыты Фарадея  Презентация на тему Выталкивающая сила
Презентация на тему Выталкивающая сила  Физическое лото (викторина 8 класс)
Физическое лото (викторина 8 класс)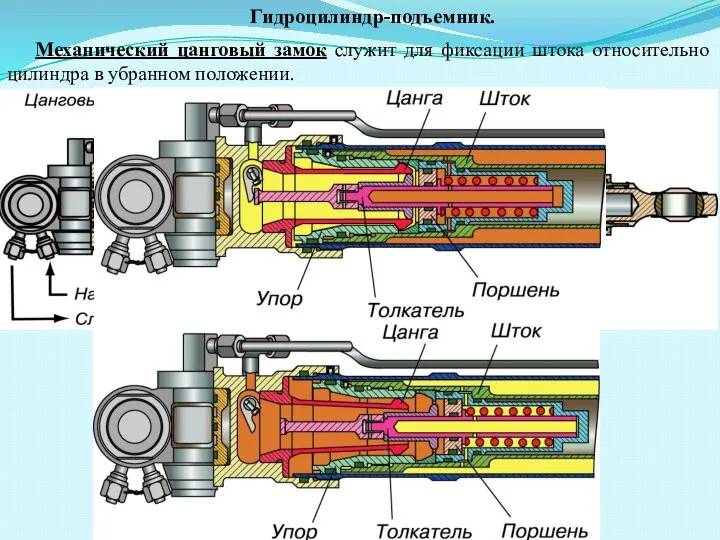 Гидроцилиндр-подъемник
Гидроцилиндр-подъемник Ford Focus II. Задняя подвеска
Ford Focus II. Задняя подвеска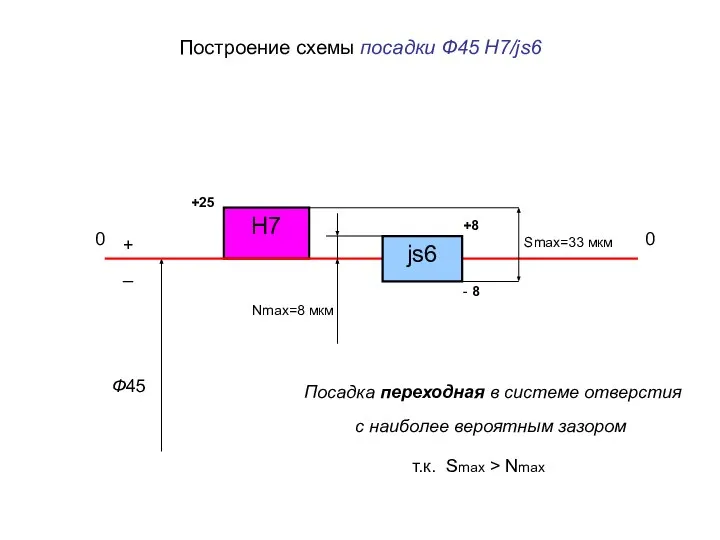 Построение схемы посадки Ф45 H7/js6
Построение схемы посадки Ф45 H7/js6 Работа, мощность, энергия. Обобщающий урок
Работа, мощность, энергия. Обобщающий урок Презентация на тему История открытия законов сохранения импульса
Презентация на тему История открытия законов сохранения импульса  Движение твердой среды
Движение твердой среды