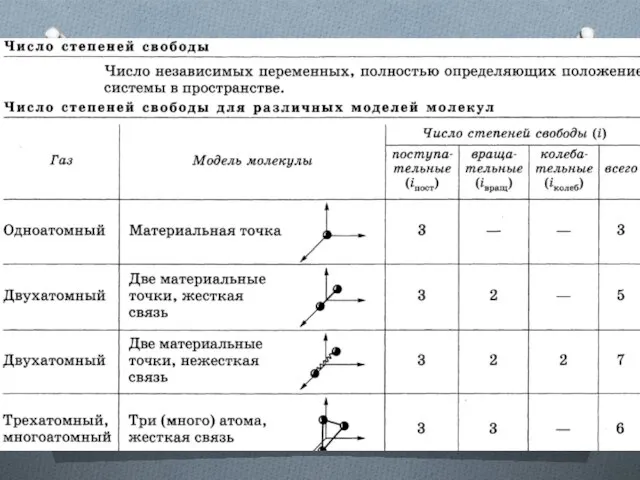
Слайд 3Энергия, приходящаяся на поступательную степень свободы
Независимо от общего числа степеней свободы

молекул три степени свободы всегда поступательные. Ни одна из поступательных степеней свободы не имеет преимущества перед другими, поэтому на каждую из них приходится в среднем одинаковая энергия, равная 1/3 значения <ε0>.
Слайд 4Закон Больцмана о равномерном распределении энергии по степеням свободы
Для статистической системы,

находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2 , а на каждую колебательную степень свободы — в среднем энергия, равная kT.
Колебательная степень «обладает» вдвое большей энергией потому, что на нее приходится не только кинетическая энергия (как в случае поступательного и вращательного движений), но и потенциальная, причем средние значения кинетической и потенциальной энергий одинаковы.
Слайд 5Средняя кинетическая энергия молекулы
i = iпост + i вращ + 2i

колеб (i — сумма числа поступательных, числа вращательных и
удвоенного числа колебательных степеней свободы молекулы)
Слайд 6Определение внутренней энергии
Энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов,

ядер и т. д.) и энергия взаимодействия этих частиц.
♦ К внутренней энергии не относятся кинетическая энергия движения системы как целого и потенциальная энергия системы во внешних полях.
Слайд 7Внутренняя энергия 1 моль идеального газа
В идеальном газе взаимная потенциальная энергия

молекул равна нулю (молекулы не взаимодействуют), поэтому Um равна сумме кинетических энергий NA молекул.
Внутренняя энергия произвольной массы m газа
Слайд 8Две формы передачи энергии от одних тел к другим
Работа и теплота.

Эти понятия имеют смысл лишь в связи с процессом изменения состояния термодинамической системы, в то время как внутренняя энергия — однозначная функция состояния этой системы.
Слайд 9Первое начало термодинамики
Первое начало термодинамики — закон сохранения и превращения энергии

применительно к термодинамическим процессам.
Слайд 10Еще одна формулировка первого начала термодинамики
Вечный двигатель первого рода невозможен.
Если

система периодически возвращается в первоначальное состояние, то изменение ее внутренней энергии ΔU = 0. Тогда, согласно первому началу термодинамики, А = Q, откуда и следует записанная формулировка.
Вечный двигатель первого рода
Периодически действующий двигатель, который совершал бы большую работу, чем сообщенная ему извне энергия.
Слайд 12Равновесный процесс
Процесс, в котором система проходит непрерывный ряд бесконечно близких термодинамически

равновесных состояний (изменение термодинамических параметров за конечный промежуток времени бесконечно мало).
♦ Все реальные процессы неравновесны (они протекают с конечной скоростью), но в ряде случаев неравновесностью реальных процессов можно пренебречь (чем медленнее процесс протекает, тем он ближе к равновесному).
Графически можно изображать только равновесные процессы.
Слайд 31Круговой процесс (цикл)
Процесс, при котором система, пройдя через ряд состояний, возвращается
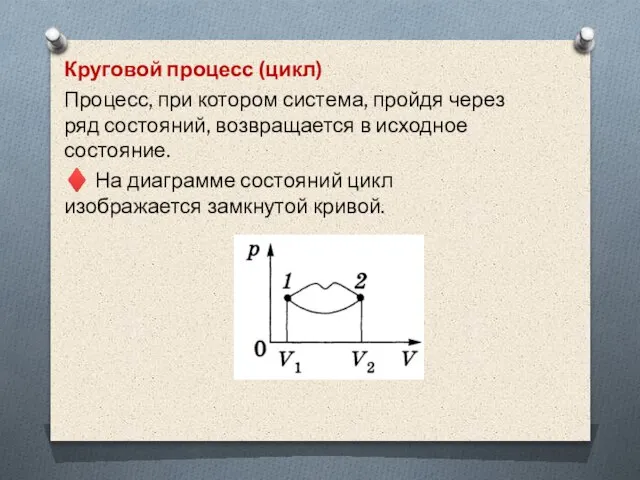
в исходное состояние.
♦ На диаграмме состояний цикл изображается замкнутой кривой.
Слайд 33Работа, совершаемая газом за цикл, определяется площадью, охватываемой замкнутой кривой.
Прямой цикл

используется в тепловых двигателях — периодически действующих двигателях, совершающих работу за счет полученной извне теплоты.
Слайд 35Работа за цикл определяется площадью, охватываемой замкнутой кривой.
Обратный цикл используется в

холодильных машинах — периодически действующих установках, в которых за счет работы внешних сил теплота переносится к телам с более высокой температурой.
Слайд 37Обратимый процесс
Термодинамический процесс, который может происходить как в прямом, так и

в обратном направлении, причем если такой процесс происходит сначала в прямом, а затем в обратном направлении и система возвращается в исходное состояние, то в окружающей среде и в этой системе не происходит никаких изменений.
Необратимый процесс
Всякий процесс, не удовлетворяющий условию обратимости процесса.
♦ Все реальные процессы необратимы, поскольку сопровождаются диссипацией энергии (из-за трения, теплопроводности и т. д.).
Слайд 38Обратимые процессы — это идеализация реальных процессов.
Их рассмотрение существенно по двум

причинам:
многие процессы в природе и технике практически обратимы;
обратимые процессы являются наиболее экономичными; имеют максимальный термический коэффициент полезного действия, что позволяет указать пути повышения КПД реальных тепловых двигателей.
Слайд 39Качественное отличие теплового движения молекул от других форм движения — его беспорядочность,

хаотичность.
Поэтому для описания теплового движения вводят количественную меру степени молекулярного беспорядка.
Приведенное количество теплоты
Отношение теплоты Q, полученной телом в изотермическом процессе, к температуре Т теплоотдающего тела.
Слайд 40Определение энтропии
Функция состояния, дифференциалом которой является
Приведенное количество теплоты, сообщаемое телу в

любом обратимом круговом процессе, равно нулю:
Полученный результат означает, что этот интеграл не зависит от пути интегрирования (последовательности промежуточных состоянии), т.е. подынтегральное выражение есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, которым система пришла в это состояние, или от предыстории системы.
Слайд 41Неравенство Клаузиуса
Энтропия замкнутой системы может либо возрастать (в случае необратимых процессов),

либо оставаться постоянной (в случае обратимых процессов).
♦ Это выражение относится только к замкнутым системам. Если система обменивается теплотой с внешней средой, то ее энтропия может вести себя любым образом.
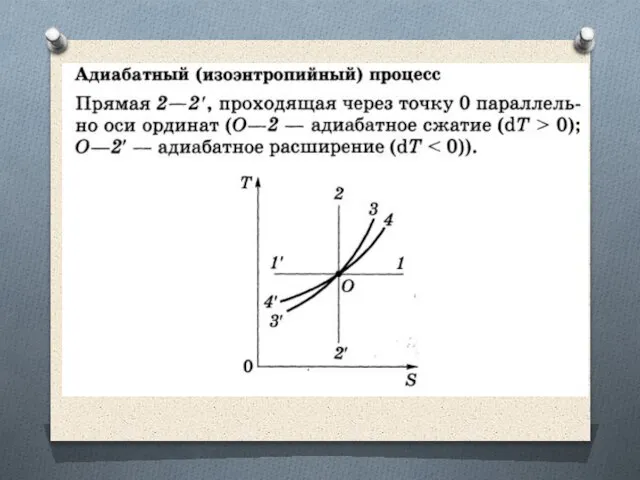
Слайд 44Изоэнтропийный процесс (S = const)
Адиабатный обратимый процесс.
Для адиабатного процесса δQ

= 0, поэтому ΔS = 0 и, следовательно, S = const, т.е. адиабатный обратимый процесс протекает при постоянной энтропии.
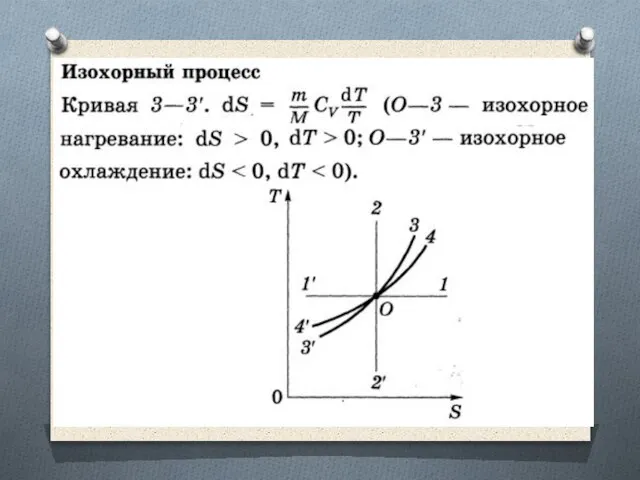
Изменение энтропии в изотермическом и изохорном процессах
Слайд 45Аддитивность энтропии
Энтропия системы равна сумме энтропии тел, входящих в систему.
Свойством

аддитивности обладают также внутренняя энергия, масса, объем (температура и давление таким свойством не обладают).
Термодинамическая вероятность (W) системы
Число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние.
♦ По определению W ≥1, т. е. термодинамическая вероятность не есть вероятность в математическом смысле (последняя ≤ 1!).
Слайд 46Формула Больцмана
Энтропия определяется логарифмом числа микросостояний, с помощью которых может быть

реализовано данное макросостояние (k —
постоянная Больцмана).
♦ Энтропия — мера вероятности состояния термодинамической системы.
Слайд 47Статистическое толкование энтропии
Энтропия является мерой неупорядоченности системы.
Чем больше число микросостояний,

реализующих данное макросостояние, тем больше энтропия.
В состоянии равновесия — наиболее вероятного состояния системы — число микросостояний максимально, при этом максимальна и энтропия.
Слайд 48Принцип возрастания энтропии
Все процессы в замкнутой системе ведут к увеличению ее

энтропии (ведь все реальные процессы необратимы).
При статистическом толковании энтропии это означает, что процессы в замкнутой системе идут в направлении увеличения числа микросостояний, иными словами, от менее вероятных состояний к более вероятным, до тех пор пока вероятность состояния не станет максимальной.
Слайд 49Согласно неравенству Клаузиуса
и формуле Больцмана (S = k In W),
энтропия и

термодинамическая вероятность состояний замкнутой системы могут либо возрастать (в случае необратимых процессов), либо оставаться постоянными (в случае обратимых процессов).
Необратимые процессы протекают самопроизвольно до тех пор, пока система не достигнет состояния, отвечающего наибольшей вероятности (энтропия при этом достигает своего максимума).
Примеры: перемешивание молекул двух газов при диффузии или выравнивание температур двух газов с разными исходными температурами.
Слайд 50Необходимость введения второго начала термодинамики
Появление второго начала термодинамики связано с необходимостью

дать ответ на вопрос, какие процессы в природе возможны, а какие нет.
Второе начало термодинамики определяет направление протекания термодинамических процессов.
Слайд 51Формулировки второго начала термодинамики
как закон возрастания энтропии при необратимых процессах
Любой

необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает или в процессах, происходящих или в замкнутой системе, энтропия не убывает.
♦ Существенно, что речь идет о замкнутых системах, так как в незамкнутых системах энтропия может вести себя любым образом.
Слайд 52по Кельвину
Невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной

от нагревателя, в эквивалентную ей работу.
по Клаузиусу
Невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому.
Слайд 53Статистическое толкование второго начала термодинамики
Возрастание энтропии означает переход системы из менее

вероятных в более вероятные состояния. Второе начало, являясь статистическим законом, описывает закономерности хаотического движения большого числа частиц, составляющих замкнутую систему.
Вечный двигатель второго рода
Периодически действующий двигатель, совершающий работу за счет одного источника теплоты.
Еще одна формулировка второго начала термодинамики
Вечный двигатель второго рода невозможен.
Слайд 54Проблема тепловой смерти Вселенной
Рассматривая Вселенную как замкнутую систему и применяя к

ней второе начало термодинамики, Клаузиус свел его содержание к утверждению, что энтропия Вселенной должна достигнуть своего максимума. Это означает, что со временем все формы движения должны перейти в тепловую.
Переход же теплоты от горячих тел к холодным приведет к тому, что температура всех тел во Вселенной сравняется, т. е. наступит полное тепловое равновесие и все процессы во Вселенной прекратятся — наступит тепловая смерть Вселенной.
Слайд 55Теорема Нернста—Планка (третье начало термодинамики)
Энтропия всех тел в состоянии равновесия стремится

к нулю по мере приближения температуры к нулю.
♦ Энтропия определяется с точностью до аддитивной постоянной, поэтому эту постоянную удобно взять равной нулю. Однако это — произвольное допущение, поскольку энтропия по своей сущности всегда определяется с точностью до аддитивной постоянной. Из теоремы Нернста— Планка следует, что теплоемкости Ср и Cv при 0 К равны нулю.
Слайд 56Принцип работы теплового двигателя
От термостата с более высокой температурой T1, называемого
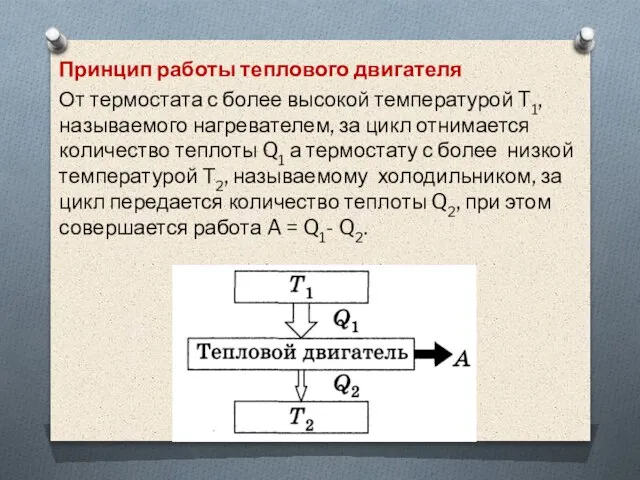
нагревателем, за цикл отнимается количество теплоты Q1 а термостату с более низкой температурой Т2, называемому холодильником, за цикл передается количество теплоты Q2, при этом совершается работа A = Q1- Q2.
Слайд 58Теорема Карно
Из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей

(Т1) и холодильников (Т2), наибольшим КПД обладают обратимые машины; при этом КПД обратимых машин, работающих при одинаковых температурах нагревателей (Т1) и холодильников (Т2), равны друг другу и не зависят от природы рабочего тела (тела, совершающего круговой процесс и обменивающегося энергией с другими телами), а определяются только температурами нагревателя и холодильника.
Слайд 59Холодильная машина
Периодически действующая установка, в которой за счет работы внешних сил

теплота переносится к телу с более высокой температурой.
Слайд 61Вывод из анализа работы холодильной машины и второе начало термодинамики
Без совершения

работы нельзя отбирать теплоту от менее нагретого тела и отдавать ее более нагретому. Это утверждение есть не что иное, как второе начало термодинамики в формулировке Клаузиуса.
♦ Второе начало термодинамики вовсе не запрещает переход теплоты от менее нагретого тела к более нагретому. Именно такой переход осуществляется в холодильной машине. Но при этом следует помнить, что внешние силы совершают работу над системой, т. е. этот переход не является единственным результатом процесса.
Слайд 62Холодильный коэффициент
Характеризует эффективность холодильной машины и определяется как отношение отнятой от

термостата с более низкой температурой количества теплоты Q2 к работе А, которая затрачивается на приведение холодильной машины в действие.
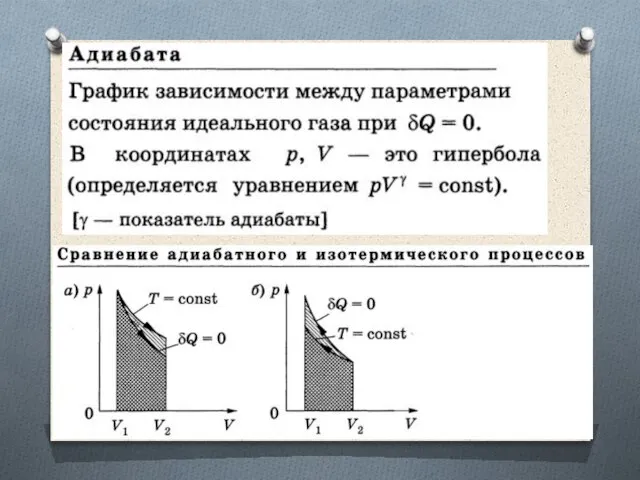
Слайд 63Цикл Карно
Наиболее экономичный обратимый круговой процесс, состоящий из двух изотерм и
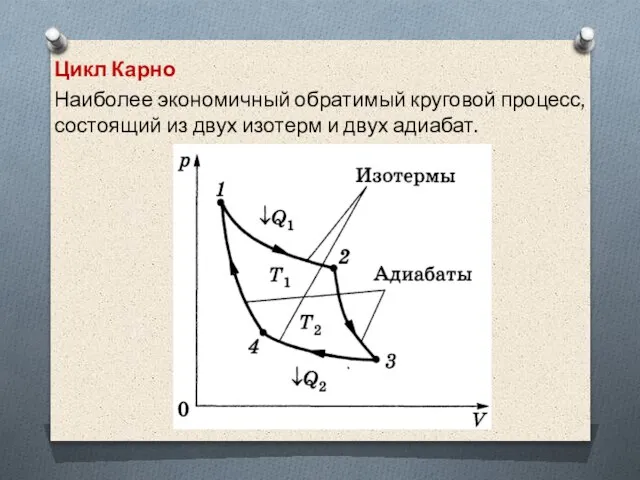
двух адиабат.
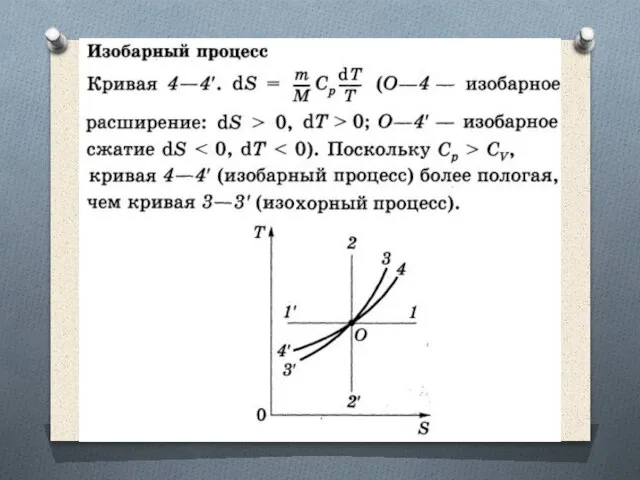
Слайд 67ТЕРМОДИНАМИЧЕСКАЯ ДИАГРАММА Т—S И ЕЕ ПРИМЕНЕНИЕ
Т — S-диаграмма. Диаграмма, где по
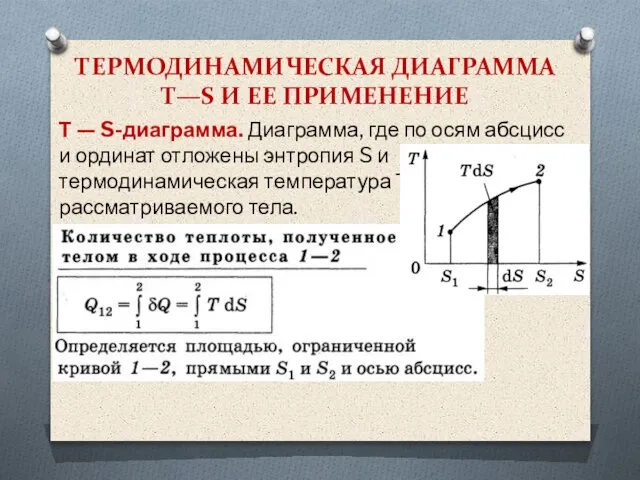
осям абсцисс и ординат отложены энтропия S и термодинамическая температура Т рассматриваемого тела.





































































 Организация исследовательской деятельности школьников на уроках физики с использованием проблемного метода обучения
Организация исследовательской деятельности школьников на уроках физики с использованием проблемного метода обучения Зеркала
Зеркала Основы теории цифровой модуляции и детектирования
Основы теории цифровой модуляции и детектирования Назначение электрооборудования автомобиля КамАЗ-53215. Выполнение работ по замене стартера
Назначение электрооборудования автомобиля КамАЗ-53215. Выполнение работ по замене стартера Физика мыльных пузырей
Физика мыльных пузырей Урок 05 Сила Ампера
Урок 05 Сила Ампера Строение атома. Опыты Резерфорда
Строение атома. Опыты Резерфорда Флот начала XX века
Флот начала XX века Практическое применение электрического тока на примере электростимуляции растений
Практическое применение электрического тока на примере электростимуляции растений Температура и ее измерение
Температура и ее измерение Резерв
Резерв Низьковимірні системи
Низьковимірні системи Массообменные процессы
Массообменные процессы Презентация на тему Золотое правило механики (7 класс)
Презентация на тему Золотое правило механики (7 класс)  Тема 10. Схема устройства и принцип работы ПД
Тема 10. Схема устройства и принцип работы ПД 10.09.2022
10.09.2022 Основы постановки научного эксперимента. ЯМР-спектроскопия. (Лекция 8)
Основы постановки научного эксперимента. ЯМР-спектроскопия. (Лекция 8) Плоская система пар сил и условие её равновесия
Плоская система пар сил и условие её равновесия Презентация по физике "Передача и использование электроэнергии" -
Презентация по физике "Передача и использование электроэнергии" -  Поиск материалов с заданными свойствами. Практическая работа
Поиск материалов с заданными свойствами. Практическая работа Основы аэродинамики
Основы аэродинамики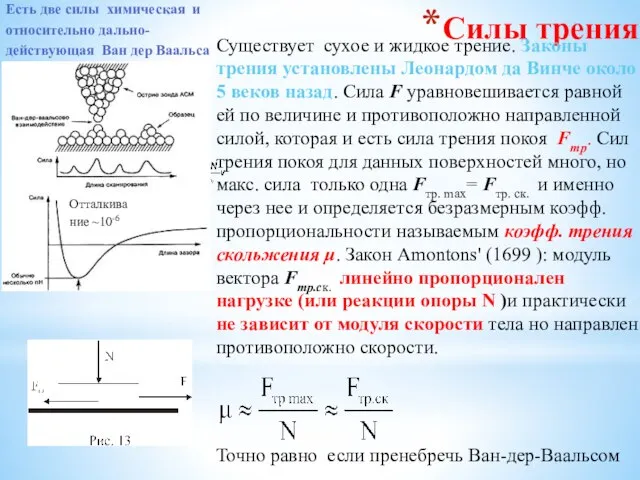 Силы трения
Силы трения Нормальные поля
Нормальные поля Задачи на определение показателей производственной программы и производственной мощности
Задачи на определение показателей производственной программы и производственной мощности Презентация на тему Агрегатное состояние вещества
Презентация на тему Агрегатное состояние вещества  Диэлектрики и проводники в электрическом поле
Диэлектрики и проводники в электрическом поле Физика вокруг нас
Физика вокруг нас Опыт Милликена. АФ1.4
Опыт Милликена. АФ1.4