Содержание
- 2. Впорядкована множина Множина, кожному елементу якої поставлений у відповідність певний номер називається впорядкованою. Будь-яку впорядковану множину,
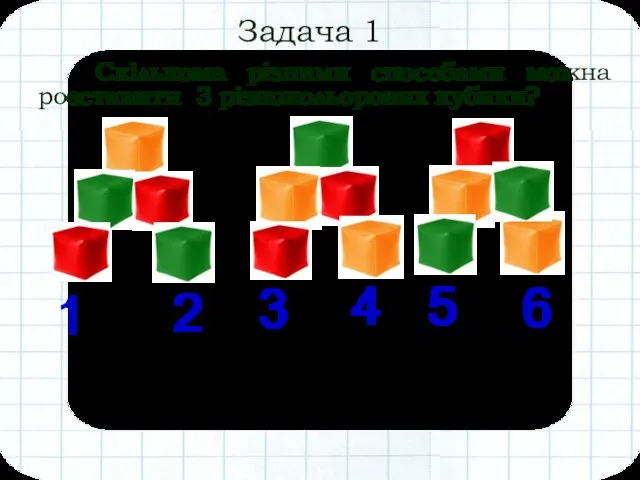
- 3. Задача 1 Скількома різними способами можна розставити 3 різнокольорових кубики? 1 2 3 4 5 6
- 4. Розділ математики, який досліджує можливі способи утворення різних підмножин з елементів деякої множини за певних умов,
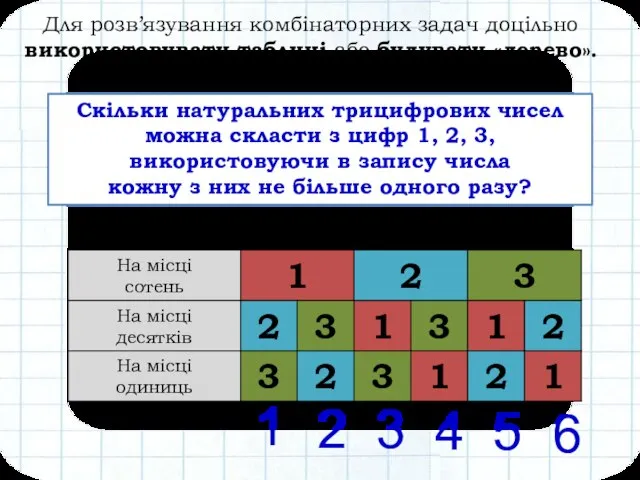
- 5. Для розв’язування комбінаторних задач доцільно використовувати таблиці або будувати «дерево». Наприклад: Скільки натуральних трицифрових чисел можна
- 6. Розглянемо розв’язування даної задачі побудовою «дерева» варіантів 1 1 1 1 1 2 2 2 2
- 7. В основі розв’язування багатьох комбінаторних задач лежать два основних правила – правило суми і правило добутку.
- 8. Правила суми і добутку можна застосовувати при виборі довільної скінченної кількості елементів. Правило суми: якщо доводиться
- 9. Перестановки множини А (позначається Pn) – це множини, що складаються з тих самих елементів, що й
- 10. Будь-яка впорядкована підмножина з k елементів даної n-елементної множини називається розміщенням з n елементів по k.
- 11. Комбінацією з n елементів по k називається будь-яка невпорядкована, k - елементна підмножина даної n -
- 12. Потренуйтеся працювати з комбінаторними формулами: 1. Обчислити: 4 6 20 4 5 3 2 2. Розв'язати
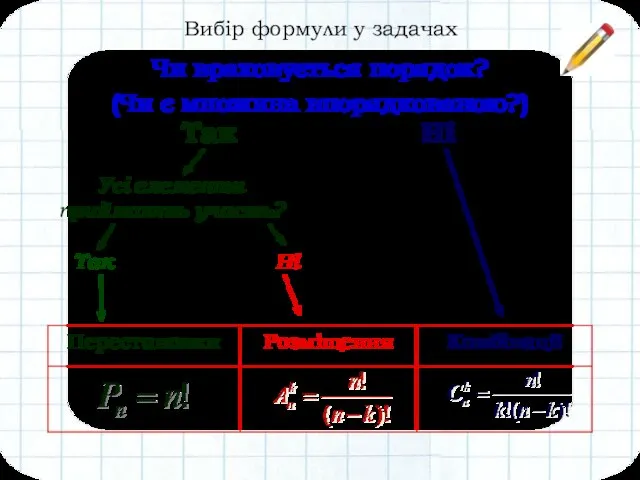
- 13. Вибір формули у задачах Чи враховується порядок? (Чи є множина впорядкованою?) Усі елементи приймають участь? Так
- 14. Потренуйтеся розв'язувати комбінаторні задачі у вигляді тестів на наступних слайдах.
- 15. З 30 учасників зборів треба вибрати голову і секретаря. Скількома способами це можна зробити? 870 30!
- 16. Скількома способами можна вибрати трьох чергових з групи в 20 чоловік? 1140 20! 6 6840 інша
- 17. Скількома способами можна вісім учнів вишикувати в колону по одному? 40320 8 256 64 інша
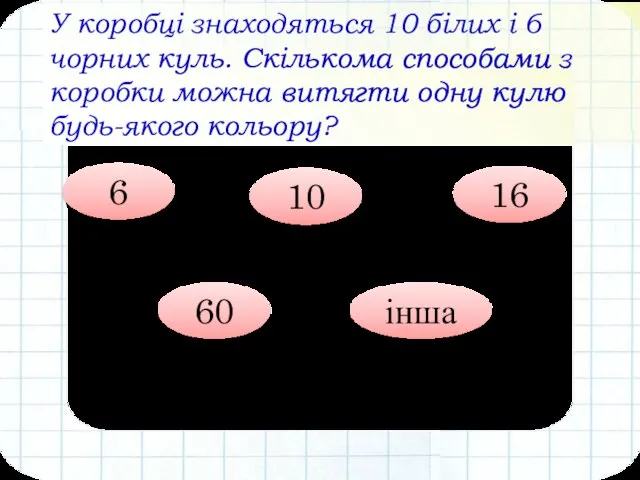
- 18. У коробці знаходяться 10 білих і 6 чорних куль. Скількома способами з коробки можна витягти одну
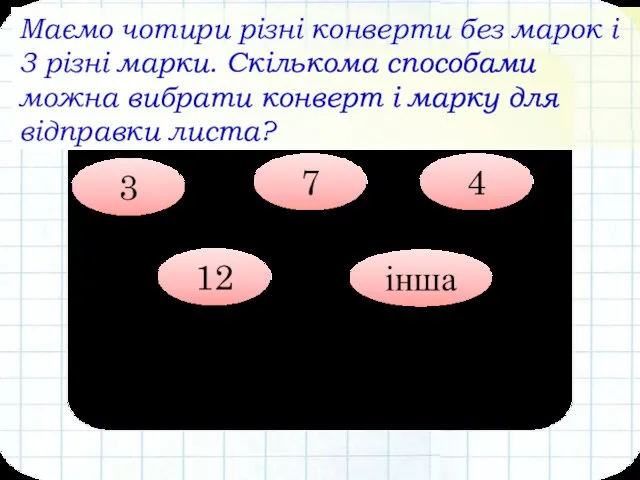
- 19. Маємо чотири різні конверти без марок і 3 різні марки. Скількома способами можна вибрати конверт і
- 21. Скачать презентацию












 Преобразование тригонометрических выражений
Преобразование тригонометрических выражений Операции, функции, выражения
Операции, функции, выражения Тригонометрические функции
Тригонометрические функции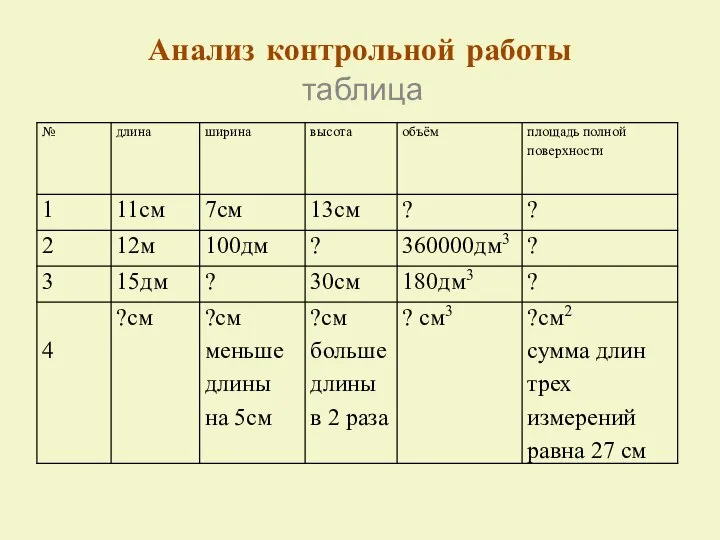 Таблицы и диаграммы. Чтение и составление таблиц
Таблицы и диаграммы. Чтение и составление таблиц Геометрические фигуры
Геометрические фигуры Текстовые задачи
Текстовые задачи Произведение многочленов
Произведение многочленов Основы тригонометрии. Радианная мера угла. Соответствие радианной и градусной мер углов
Основы тригонометрии. Радианная мера угла. Соответствие радианной и градусной мер углов Золотое сечение - божественная мера красоты
Золотое сечение - божественная мера красоты Практическая работа. Решение задач по темам: Давление твердых тел, жидкостей и газов, закон Архимеда, плавание тел
Практическая работа. Решение задач по темам: Давление твердых тел, жидкостей и газов, закон Архимеда, плавание тел Презентация на тему Угол. Прямой и развернутый угол
Презентация на тему Угол. Прямой и развернутый угол  Задача о трех игральных костях. Элементарный способ
Задача о трех игральных костях. Элементарный способ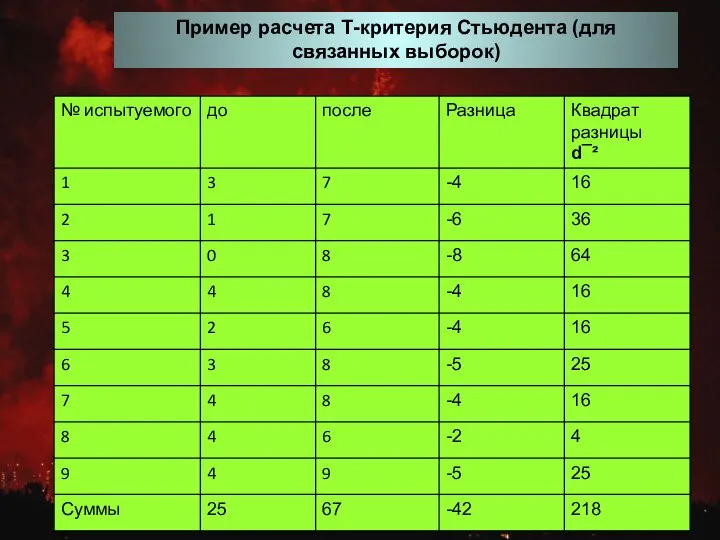 Пример расчета Т-критерия Стьюдента (для связанных выборок)
Пример расчета Т-критерия Стьюдента (для связанных выборок) Решите систему неравенств и укажите все целые числа, которые являются ее решениями
Решите систему неравенств и укажите все целые числа, которые являются ее решениями Прямоугольная система координат в пространстве. Координаты середины отрезка. Расстояние между двумя точками. Уравнение сферы
Прямоугольная система координат в пространстве. Координаты середины отрезка. Расстояние между двумя точками. Уравнение сферы Буквенная запись свойств действий над числами
Буквенная запись свойств действий над числами Отношение чисел
Отношение чисел ЛЕКЦИЯ_7
ЛЕКЦИЯ_7 Обыкновенные дроби. Тест с заполнением пропусков
Обыкновенные дроби. Тест с заполнением пропусков Множественная регрессия в экономике
Множественная регрессия в экономике Путешествие в страну Математику
Путешествие в страну Математику Сумма и разность синусов, косинусов
Сумма и разность синусов, косинусов Параллельные прямые
Параллельные прямые Предел функции
Предел функции Число и цифра 0. Сложение и вычитание с числом 0
Число и цифра 0. Сложение и вычитание с числом 0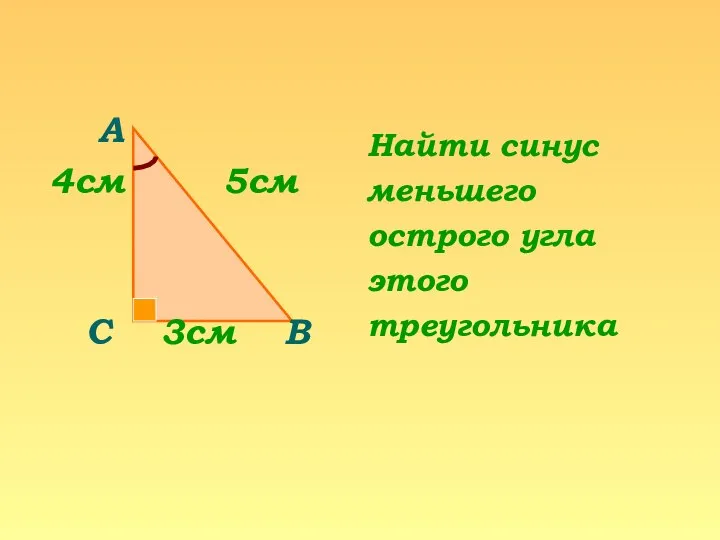 Устная работа на уроке геометрии
Устная работа на уроке геометрии Графики функций
Графики функций Центральные и вписанные углы. Решение задач
Центральные и вписанные углы. Решение задач