Содержание
- 2. Фундаментальные взаимодействия В основе всех физических явлений лежит взаимодействие между углами или частицами, участвующими в этих
- 3. 1. Электрический заряд Электромагнитное взаимодействие – фундаментальное взаимодействие, в котором участвуют частицы, имеющие электрический заряд. Взаимодействие
- 4. 1. Электрический заряд Величина элементарного заряда равна в СИ: Тела, не участвующие в электрическом взаимодействии, называются
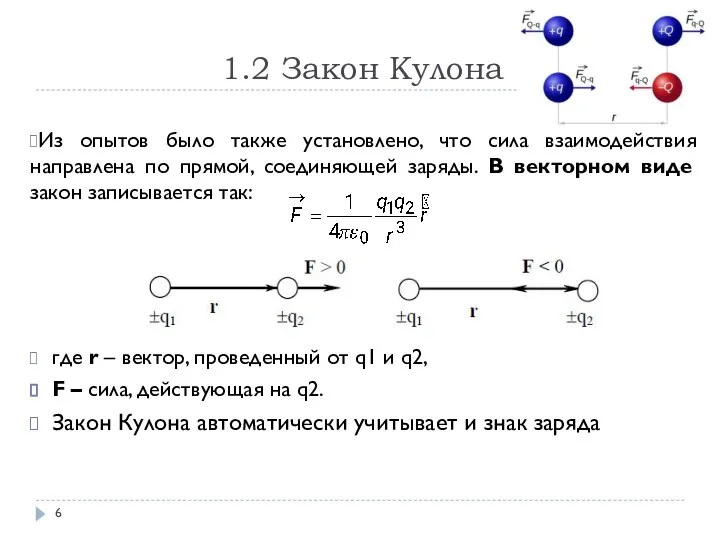
- 5. 1.2 Закон Кулона
- 6. 1.2 Закон Кулона Из опытов было также установлено, что сила взаимодействия направлена по прямой, соединяющей заряды.
- 7. 1.3 Электрическое поле
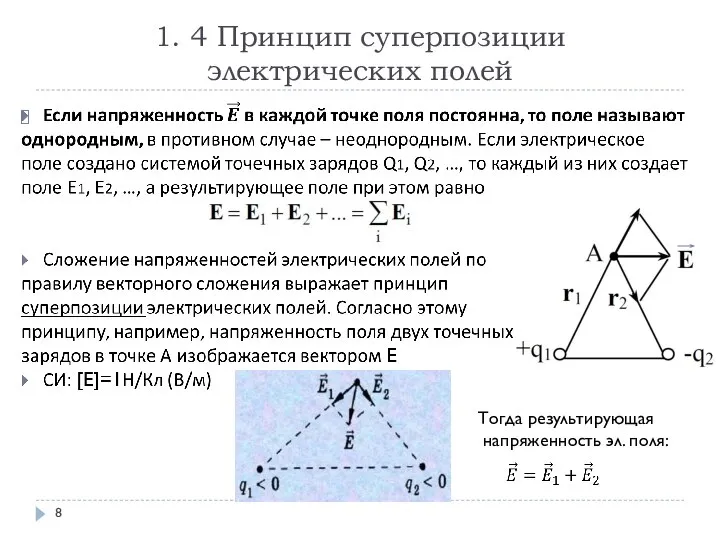
- 8. 1. 4 Принцип суперпозиции электрических полей Тогда результирующая напряженность эл. поля:
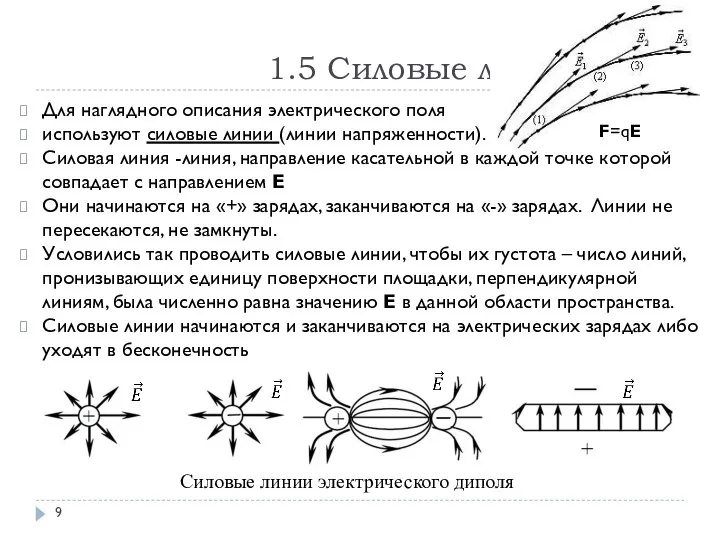
- 9. 1.5 Силовые линии. Для наглядного описания электрического поля используют силовые линии (линии напряженности). Силовая линия -линия,
- 10. 1.6 Распределение зарядов Если заряд непрерывно распределен внутри макроскопического тела, его пространственное распределение описывают плотности: Линейная
- 11. 1.6 Примеры Значение напряженности электрического поля E, созданного точечным зарядом q, на расстоянии r от заряда
- 12. 1.7. Поток вектора напряженности Если вектора E и n образуют острый угол, поток положительный.
- 13. 1.8 Теорема Гаусса Основное соотношение между источником и полем можно выразить с помощью потока вектора напряженности
- 14. 1.8 Теорема Гаусса Этот результат обобщается на произвольную замкнутую поверхность, охватывающую заряд Q: поток вектора напряженности
- 15. 1.8 Применение теоремы Гаусса Применяется для расчета электрических полей в задачах со специальной симметрией. 1. Напряженность
- 16. 1.8 Применение теоремы Гаусса 3. Напряженность электрического поля цилиндра (нити) радиусом R, равномерно заряженного с линейной
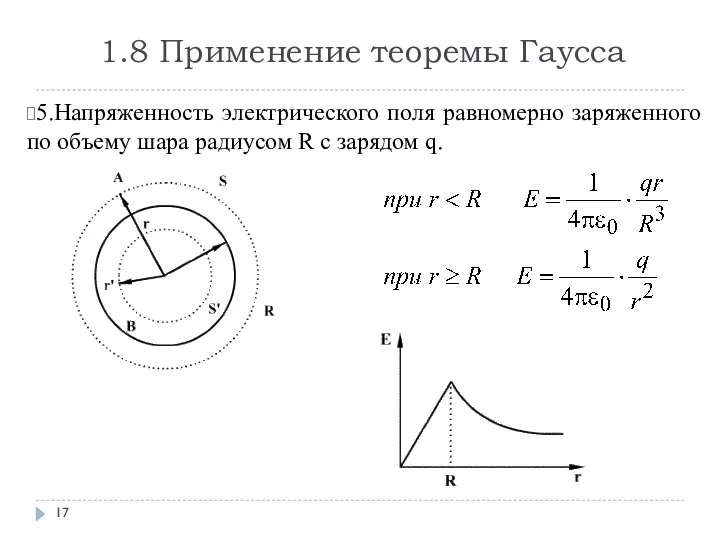
- 17. 1.8 Применение теоремы Гаусса 5.Напряженность электрического поля равномерно заряженного по объему шара радиусом R с зарядом
- 18. 1.7 Вычисление напряженности поля бесконечно заряженной плоскости . напряженность поля бесконечно заряженной плоскости с поверхностной плотностью
- 19. 2.1 Работа сил электрического поля Найдем работу, совершаемую электрическими силами поля заряда Q при перемещении заряда
- 20. 2.2. Потенциал электрического поля СИ:[φ]= 1B=1Дж/Кл
- 21. 2.3 Связь потенциала с напряженностью поля Работа по перемещению заряда q из точки 1 в точку
- 22. 2.4 Связь потенциала с напряженностью поля Вычислим потенциал поля, созданного равномерно заряженной бесконечной плоскостью: Напряженность поля
- 24. Скачать презентацию














![2.2. Потенциал электрического поля СИ:[φ]= 1B=1Дж/Кл](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1078766/slide-19.jpg)


 Зеркало
Зеркало Суперпроводники. История открытия
Суперпроводники. История открытия Физический диктант
Физический диктант Движение системы тел с учётом трения
Движение системы тел с учётом трения Пара сил и момент силы относительно точки
Пара сил и момент силы относительно точки Ворот-разновидность рычага
Ворот-разновидность рычага Расчёт аэродинамических характеристик дозвуковых самолётов (Лекция 1)
Расчёт аэродинамических характеристик дозвуковых самолётов (Лекция 1) Презентация на тему Температура
Презентация на тему Температура  Исследование изменения со временем температуры остывающей воды
Исследование изменения со временем температуры остывающей воды Шумоподавляющие фильтры
Шумоподавляющие фильтры Двигуни внутрішнього згоряння
Двигуни внутрішнього згоряння Прозрачный люминесцентный солнечный концентратор
Прозрачный люминесцентный солнечный концентратор Техническое обслуживание и ремонт электрических машин постоянного и переменного тока. Тест
Техническое обслуживание и ремонт электрических машин постоянного и переменного тока. Тест Использование дозиметра-радиометра АНРИ-01-02 Сосна для контроля радиационной обстановки
Использование дозиметра-радиометра АНРИ-01-02 Сосна для контроля радиационной обстановки Электрооборудование двигателя
Электрооборудование двигателя Определение скоростей и ускорений точек АТТ при плоском движении
Определение скоростей и ускорений точек АТТ при плоском движении Математический и пружинный маятники
Математический и пружинный маятники Ядерный (атомный) реактор
Ядерный (атомный) реактор Комплексный потенциал и комплексная скорость. Некоторые простейшие потенциальные потоки. Условия подобия
Комплексный потенциал и комплексная скорость. Некоторые простейшие потенциальные потоки. Условия подобия Радиолокация
Радиолокация Закон сохранения энергии
Закон сохранения энергии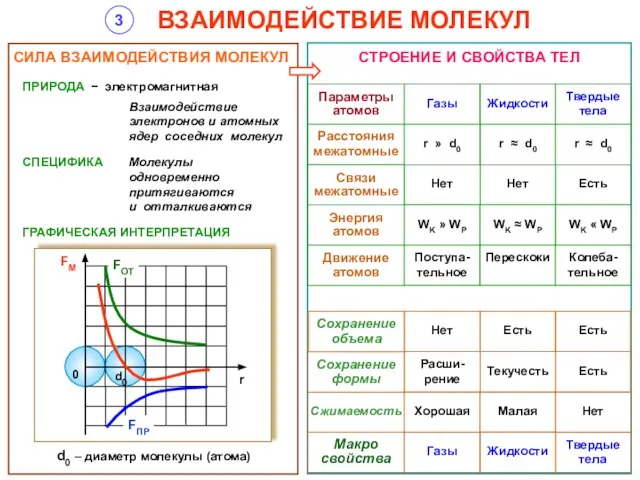 Взаимодействие молекул
Взаимодействие молекул Термическое разупрочнение деформированного металла
Термическое разупрочнение деформированного металла Презентация на тему Звуковые волны
Презентация на тему Звуковые волны  Рабочие режимы электроэнергетических систем. Методы и средства регулирования рабочих режимов
Рабочие режимы электроэнергетических систем. Методы и средства регулирования рабочих режимов Урок физики в 10 классе. Равномерное прямолинейное движение
Урок физики в 10 классе. Равномерное прямолинейное движение Электрическое сопротивление проводника. Удельное сопротивление
Электрическое сопротивление проводника. Удельное сопротивление Доклад о История водоплавания
Доклад о История водоплавания