Магнитное поле. Лекция 19. Закон Био-Савара-Лапласа. Теорема о циркуляции вектора магнитной индукции
Содержание
- 2. Электрическое поле – одна из сторон электромагнитного поля, создаваемая электрическими зарядами и изменяющимся магнитным полем и
- 3. Опыт Эрстеда Эрстед помещал над магнитной стрелкой прямолинейный металлический проводник, направленный параллельно стрелке. При пропускании через
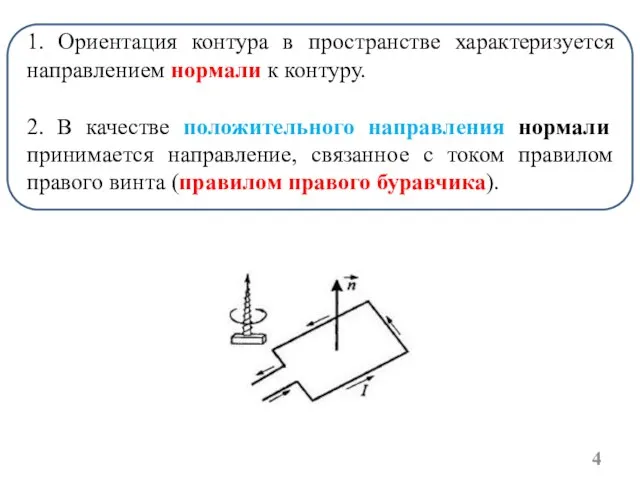
- 4. 1. Ориентация контура в пространстве характеризуется направлением нормали к контуру. 2. В качестве положительного направления нормали
- 5. 3. Магнитное поле оказывает на рамку с током ориентирующее действие, поворачивая её определённым образом. За направление
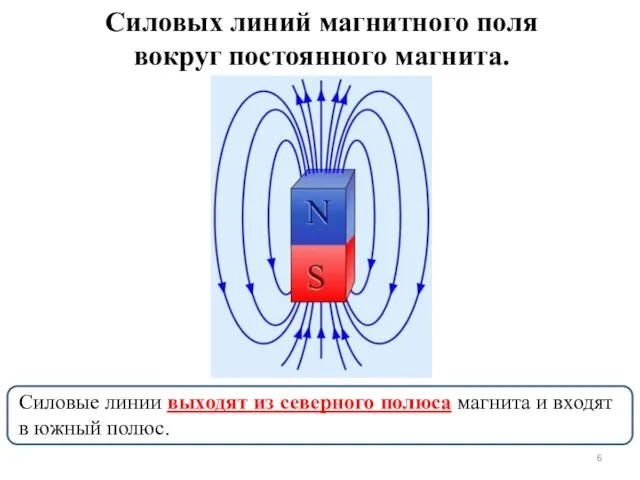
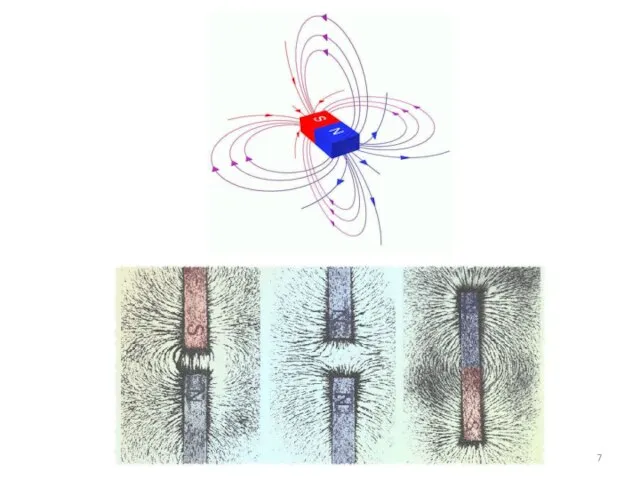
- 6. Силовые линии выходят из северного полюса магнита и входят в южный полюс. Cиловых линий магнитного поля
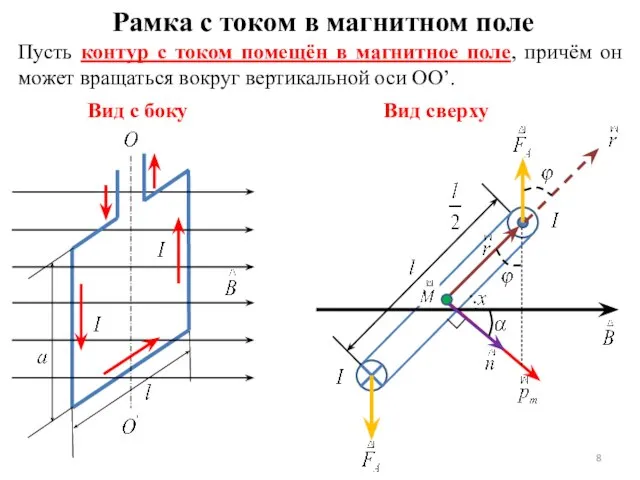
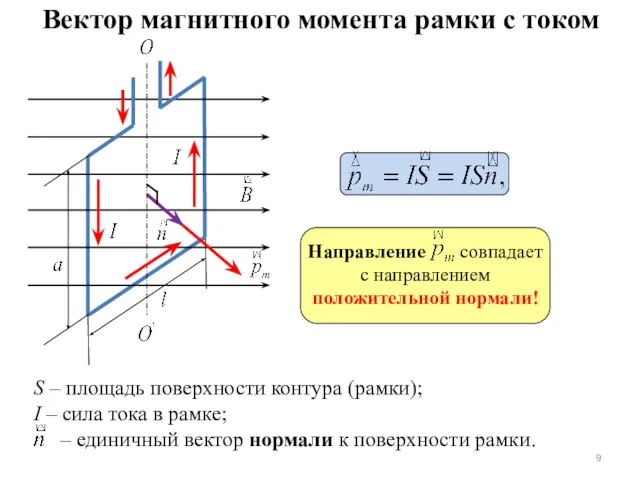
- 8. Пусть контур с током помещён в магнитное поле, причём он может вращаться вокруг вертикальной оси OO’.
- 9. S – площадь поверхности контура (рамки); I – сила тока в рамке; – единичный вектор нормали
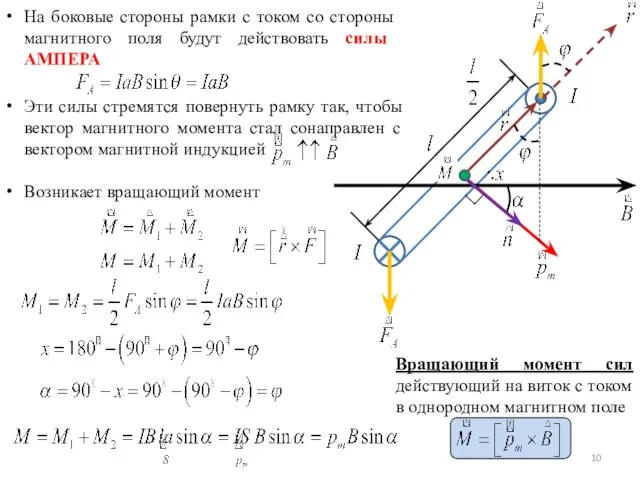
- 10. На боковые стороны рамки с током со стороны магнитного поля будут действовать силы АМПЕРА Эти силы
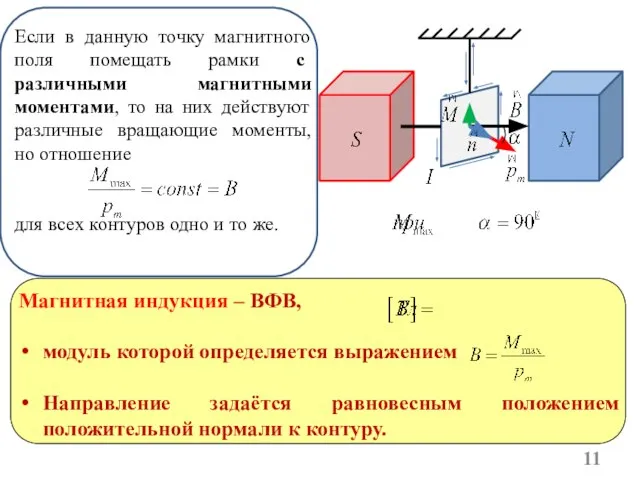
- 11. Если в данную точку магнитного поля помещать рамки с различными магнитными моментами, то на них действуют
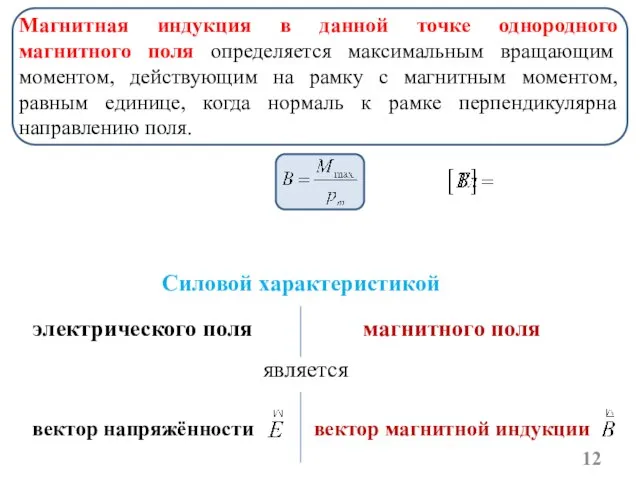
- 12. Магнитная индукция в данной точке однородного магнитного поля определяется максимальным вращающим моментом, действующим на рамку с
- 13. Линии магнитной индукции всегда замкнуты и охватывают проводники с током. электрического поля магнитного поля Силовые линии
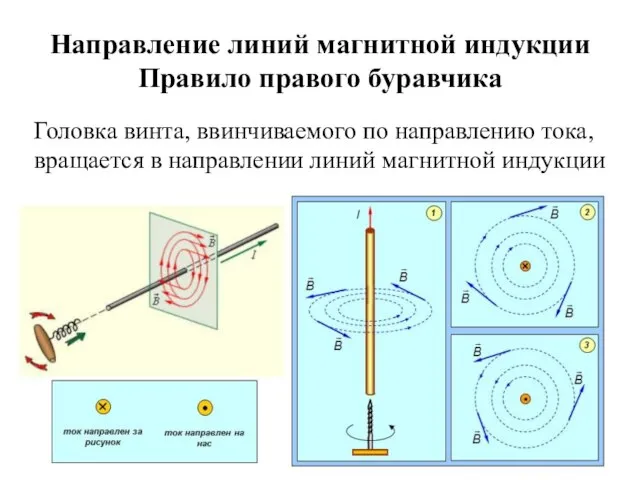
- 14. Направление линий магнитной индукции Правило правого буравчика Головка винта, ввинчиваемого по направлению тока, вращается в направлении
- 15. 1. магнитное поле действует на движущиеся заряды (электрический ток); 2. движущиеся заряды (электрический ток) создают магнитное
- 17. Магнитная индукция результирующего поля, создаваемого несколькими токами (движущимися зарядами), равна векторной сумме магнитных индукций полей, создаваемых
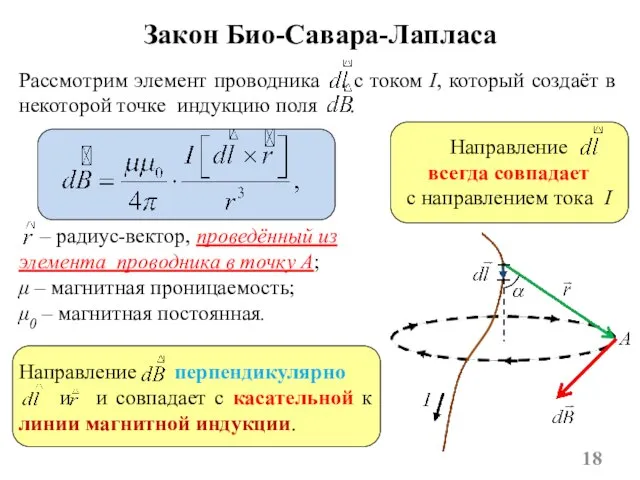
- 18. Закон Био-Савара-Лапласа – радиус-вектор, проведённый из элемента проводника в точку А; μ – магнитная проницаемость; μ0
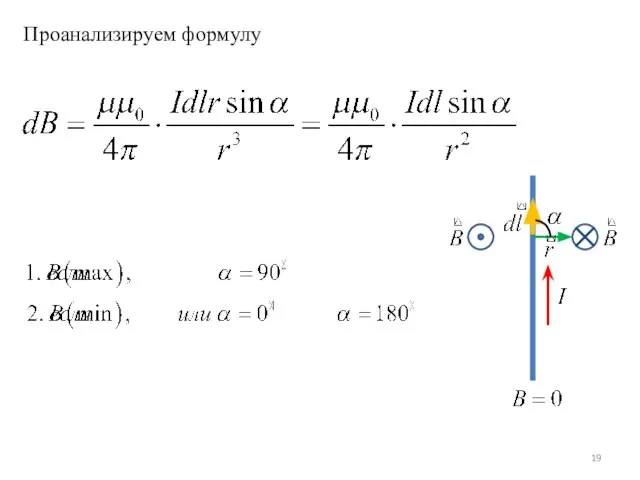
- 19. Проанализируем формулу
- 20. Модуль вектора определяется выражением (для вакуума). Био Жан Батист 1774 - 1862 Лаплас Пьер Симон 1749
- 21. Примеры расчёта некоторых магнитных полей Прямой проводник бесконечной длины создаёт магнитное поле вокруг себя. Рассчитаем величину
- 22. В качестве переменной интегрирования выберем угол α, выразив через него все остальные величины: Подставляем полученные выражения
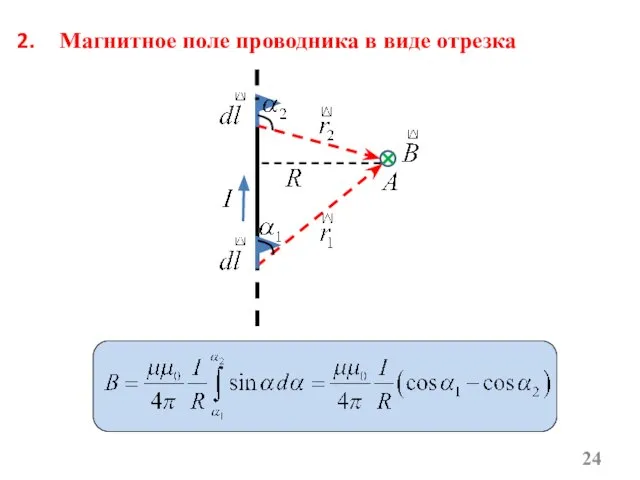
- 24. Магнитное поле проводника в виде отрезка
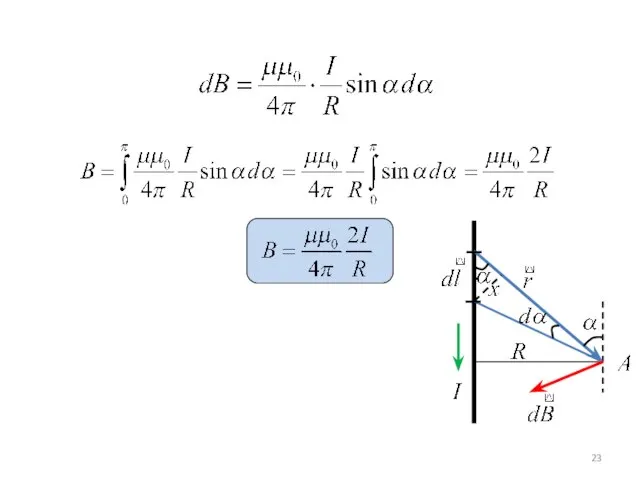
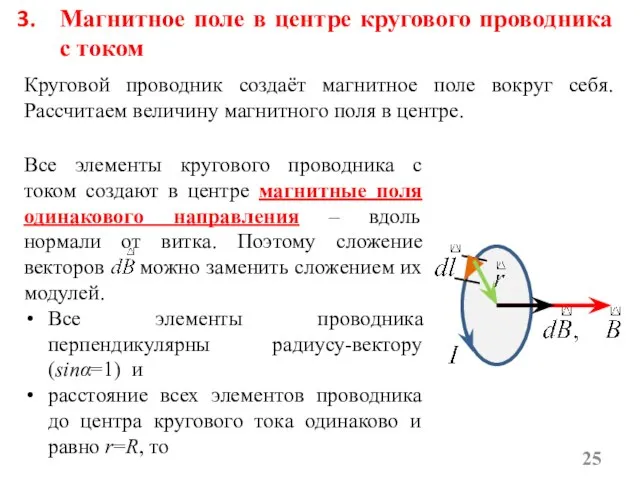
- 25. Круговой проводник создаёт магнитное поле вокруг себя. Рассчитаем величину магнитного поля в центре. Магнитное поле в
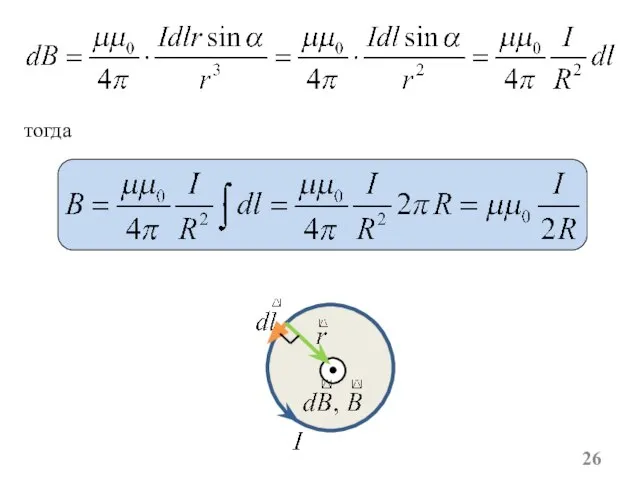
- 26. тогда
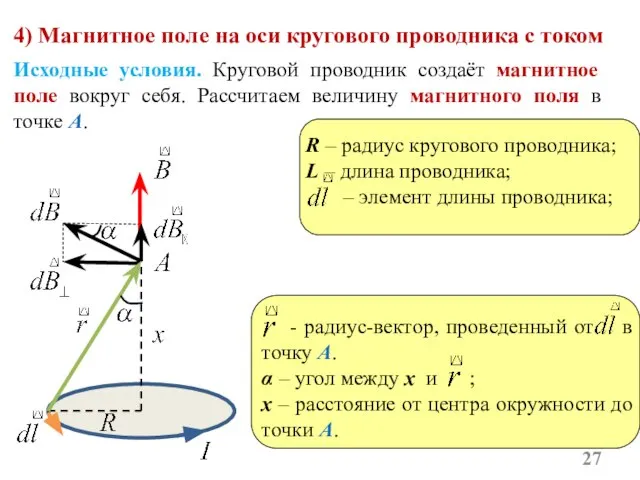
- 27. Исходные условия. Круговой проводник создаёт магнитное поле вокруг себя. Рассчитаем величину магнитного поля в точке A.
- 28. На расстоянии r от центра витка вдоль оси витка, магнитное поле будет равно
- 29. Вектор напряжённости магнитного поля Макроскопические токи – электрические токи, протекающие по проводникам в электрических цепях. Микроскопические
- 30. Связь между векторами магнитной индукции и напряжённостью магнитного поля Для однородной изотропной среды вектор магнитной индукции
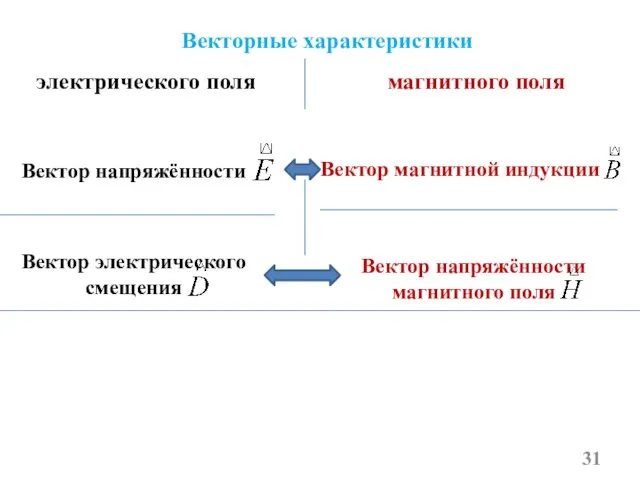
- 31. электрического поля магнитного поля Векторные характеристики Вектор напряжённости Вектор магнитной индукции Вектор электрического смещения Вектор напряжённости
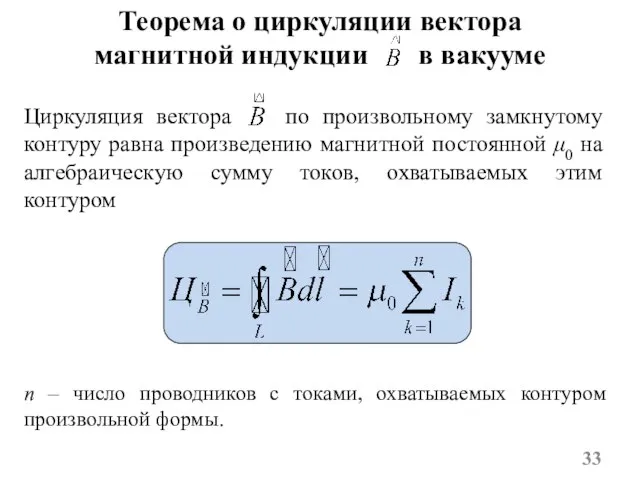
- 32. Циркуляция вектора магнитной индукции Циркуляцией вектора по замкнутому контуру L называется следующий интеграл по этому контуру:
- 33. Циркуляция вектора по произвольному замкнутому контуру равна произведению магнитной постоянной μ0 на алгебраическую сумму токов, охватываемых
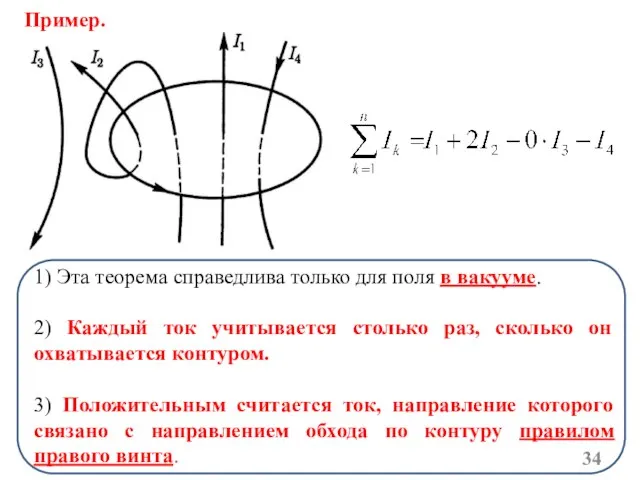
- 34. 1) Эта теорема справедлива только для поля в вакууме. 2) Каждый ток учитывается столько раз, сколько
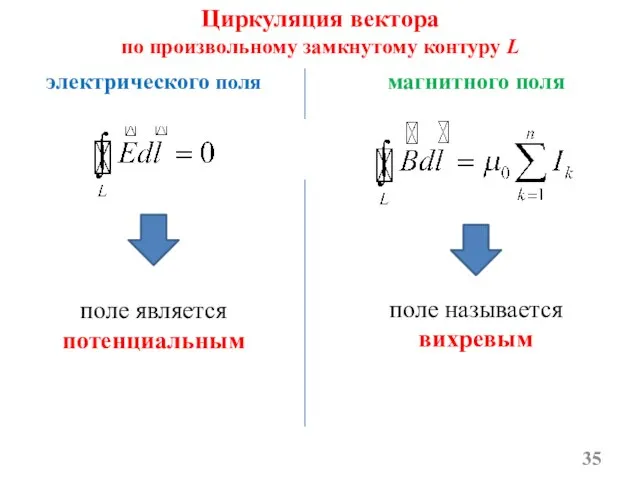
- 35. электрического поля магнитного поля Циркуляция вектора по произвольному замкнутому контуру L поле является потенциальным поле называется
- 36. Примеры применения теоремы о циркуляции вектора Магнитное поле прямого тока Замкнутый контур представлен в виде окружности
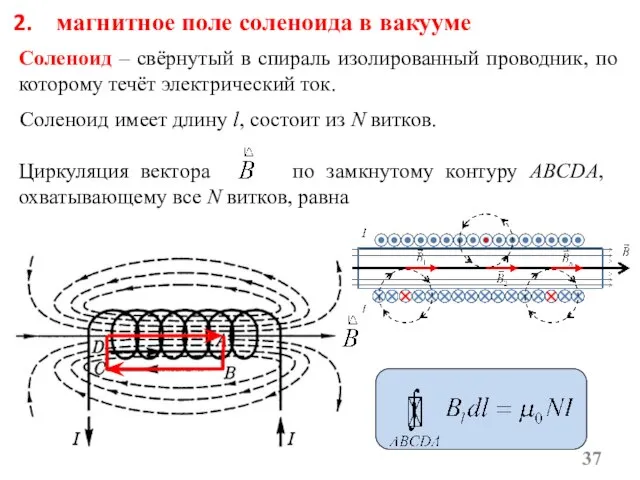
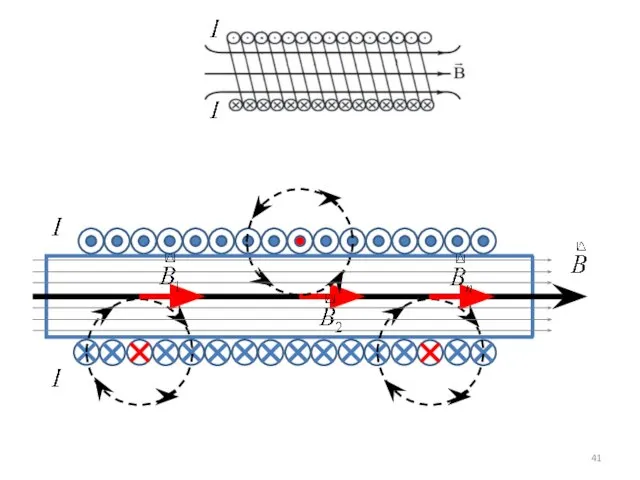
- 37. магнитное поле соленоида в вакууме Соленоид – свёрнутый в спираль изолированный проводник, по которому течёт электрический
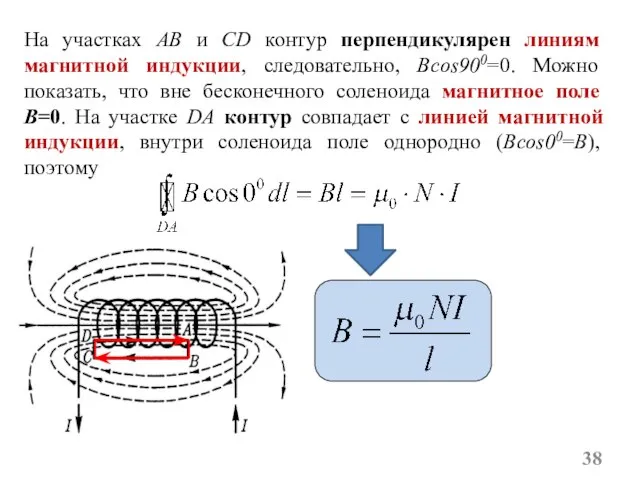
- 38. На участках AB и CD контур перпендикулярен линиям магнитной индукции, следовательно, Bcos900=0. Можно показать, что вне
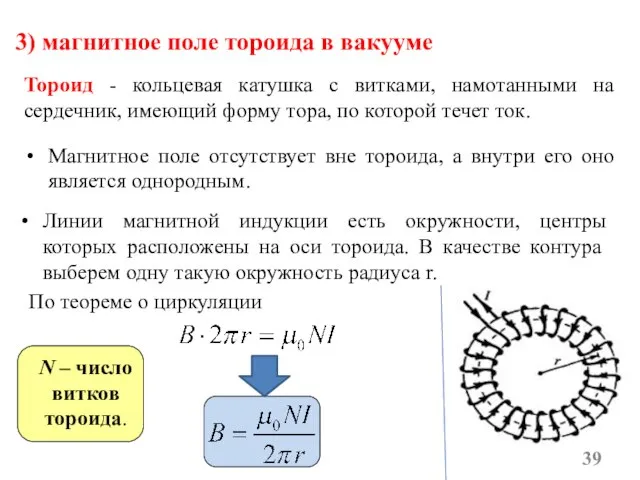
- 39. 3) магнитное поле тороида в вакууме Тороид - кольцевая катушка с витками, намотанными на сердечник, имеющий
- 43. Скачать презентацию















 Процессоры. История создания процессора
Процессоры. История создания процессора ТЕМА: Алюминий, его физические и химические свойства ЦЕЛЬ: рассмотреть физические и химические свойства алюминия, особенности стр
ТЕМА: Алюминий, его физические и химические свойства ЦЕЛЬ: рассмотреть физические и химические свойства алюминия, особенности стр Методы исследования частиц
Методы исследования частиц Сила
Сила Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц Диагностика электронных систем управления бензиновых двигателей
Диагностика электронных систем управления бензиновых двигателей Магнитное поле Земли
Магнитное поле Земли Акустический метод диагностирования электрооборудования
Акустический метод диагностирования электрооборудования Температура плавления нанокластеров. Методика определения фактора Дебая-Валлера по интенсивности спектров СРЭО
Температура плавления нанокластеров. Методика определения фактора Дебая-Валлера по интенсивности спектров СРЭО Динамика. Подготовка к ЕГЭ
Динамика. Подготовка к ЕГЭ Сила
Сила Определение показателя преломления стекла
Определение показателя преломления стекла etalon_otredaktirovana_LEKTsIYa_8_ioniziruyuschee_ETALON
etalon_otredaktirovana_LEKTsIYa_8_ioniziruyuschee_ETALON Измерительная система определения теплофизических свойств твердых и сыпучих материалов на базе прибора ИТ – 3
Измерительная система определения теплофизических свойств твердых и сыпучих материалов на базе прибора ИТ – 3 Закон Ома. Сформулируйте этот закон
Закон Ома. Сформулируйте этот закон Нелинейные электрические цепи
Нелинейные электрические цепи Потенциал электрического поля. Разность потенциалов
Потенциал электрического поля. Разность потенциалов Закон Кеплера
Закон Кеплера ЭЛЕКТРИЧЕСТВО В БЫТУ
ЭЛЕКТРИЧЕСТВО В БЫТУ Пара сил и момент силы относительно точки
Пара сил и момент силы относительно точки Мощность. Единицы мощности
Мощность. Единицы мощности Основы технической гидромеханики
Основы технической гидромеханики Сила Лоренца
Сила Лоренца Емкостное и индуктивное сопротивления переменного тока. Закон Ома для электрической цепи переменного тока
Емкостное и индуктивное сопротивления переменного тока. Закон Ома для электрической цепи переменного тока Устройство системы смазки двигателя. Назначение общее устройство системы смазки автомобильных двигателей
Устройство системы смазки двигателя. Назначение общее устройство системы смазки автомобильных двигателей Первые рычаги
Первые рычаги Ветровой электрогенератор challenergy
Ветровой электрогенератор challenergy Л2.1. Твёрдость металлов
Л2.1. Твёрдость металлов