Оптимальное обнаружение сигнала с полностью известными параметрами

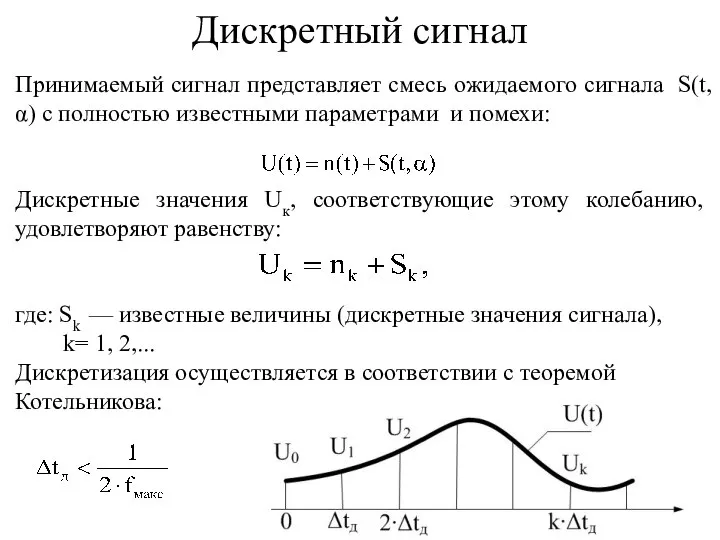
Принимаемый сигнал представляет смесь ожидаемого сигнала S(t,α) с полностью известными параметрами и помехи:
Дискретные значения Uк, соответствующие этому колебанию, удовлетворяют равенству:
где: Sk — известные величины (дискретные значения сигнала),
k= 1, 2,...
Дискретизация осуществляется в соответствии с теоремой Котельникова:
Дискретный сигнал

Hаличие сигнала приводит к смещению распределения величины Uk относительно распределения без сигнала Uk= nk:
Отношение правдоподобия для известного :
Отсчеты белого шума распределены по нормальному закону, некоррелированны и статистически независимы, соответственно:
Распределение шума и сигнала

Отношение правдоподобия
Осуществим предельный переход , fмакс→∞, ∆t→0, получим:
Запишем корреляционный интеграл:
Окончательно отношение правдоподобия может быть представлено в виде:

Отношение правдоподобия - монотонная функция корреляционного интеграла для реализации U(t) и ожидаемого сигнала с параметрами α.
Сравнение отношения правдоподобия с порогом l0 эквивалентно сравнению корреляционного интеграла с соответствующим порогом z0:
где: N0 – спектральная плотность шума;
E(α) – энергия ожидаемого сигнала.
Алгоритм работы оптимального обнаружителя:
вычислять корреляционный интеграл или его монотонную функцию;
сравнивать результат с порогом.
Алгоритм обнаружения известного сигнала

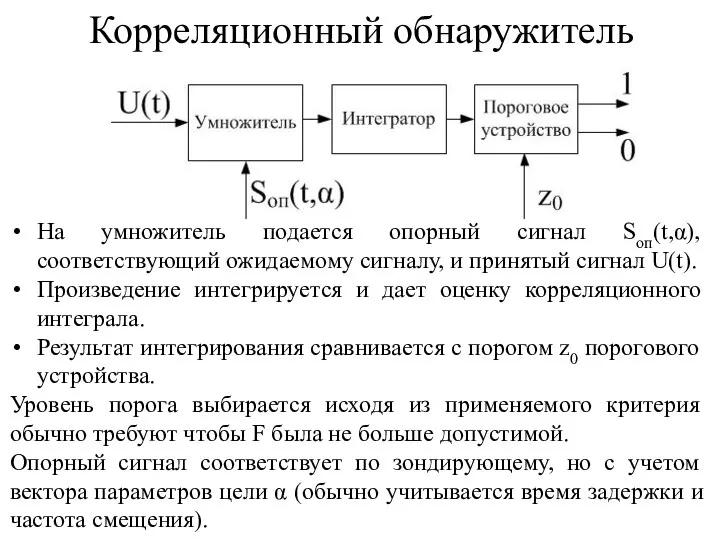
Корреляционный обнаружитель
На умножитель подается опорный сигнал Sоп(t,α), соответствующий ожидаемому сигналу, и принятый сигнал U(t).
Произведение интегрируется и дает оценку корреляционного интеграла.
Результат интегрирования сравнивается с порогом z0 порогового устройства.
Уровень порога выбирается исходя из применяемого критерия обычно требуют чтобы F была не больше допустимой.
Опорный сигнал соответствует по зондирующему, но с учетом вектора параметров цели α (обычно учитывается время задержки и частота смещения).

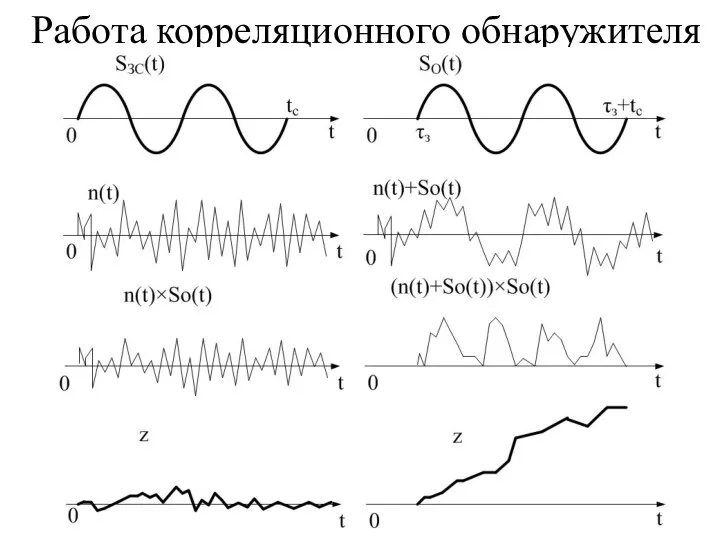
Работа корреляционного обнаружителя

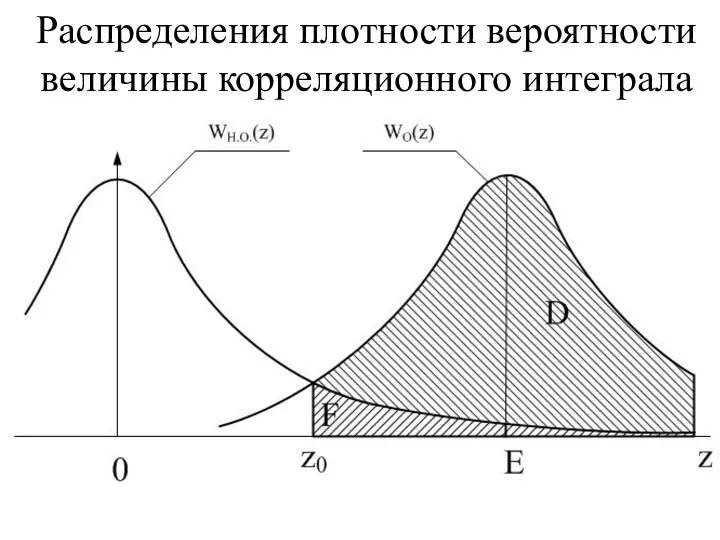
Распределения плотности вероятности величины корреляционного интеграла

Положим, что сигнал принимается М-элементной антенной решеткой, элементы которой расположены в одном или нескольких пунктах приема, тогда совокупность всех принятых сигналов описывается вектор–столбцом U(t):
Реализация принимаемых колебаний:
α – вектор информативных параметров сигнала (задержка, частота смещения, угловые координаты источника излучения);
β – вектор неинформативных случайных параметров сигнала (начальная фаза, амплитуда, совокупность случайных фаз и амплитуд, параметры случайной поляризации сигнала);
ν – вектор случайных параметров помехи.
Задача многоканального обнаружения

После дискретизации сигнала, получим L временных дискрет для каждой функции Ui(t). Тогда общее число дискрет при М-канальном приеме i = 1, 2,…,М составит m = L·M, решение принимается по M-мерному вектор-столбцу:
Сигнал обозначим вектором S = ||Si||, размерность которого определяется общим числом временных дискрет во всех антенных каналах:
Помеху обозначим вектор-столбцом n = ||ni|| случайных значений. Мат. ожидание каждого из них равно нулю: M{ni} = 0.
Мат. ожидание n также равно нулю: M{n} = 0, а его элементы распределены по гауссовскому (нормальному) закону:
Влияние дискретизации сигнала

Помеха в общем случае считается нестационарной: различные элементы выборки ni и nk помехи могут иметь различные дисперсии σi и быть взаимозависимы, так что их центрированный корреляционный момент, называемый ковариацией в общем случае не равен нулю:
Степень взаимной корреляции характеризуют обычно коэффициентом корреляции элементов помеховой выборки
Величина ρik изменяется от +1 до -1.
Значения ρik равны ±1, когда величины ni и nk пропорциональны. Знак плюс соответствует положительному, а знак минус — отрицательному коэффициенту пропорциональности.
Учет нестационарных помех

Совокупность корреляционных моментов (ковариаций) элементов помеховой выборки образует прямоугольную корреляционную или ковариационную матрицу в зависимости от смещенности или неспещенности случайных процессов:
Диагональными элементами корреляционной матрицы оказываются дисперсии элементов выборки: ψii = σi2.
Для ковариационной матриы можно найти определитель и матрицу, соответственно можно найти плотность вероятности эквивалентного гауссовского закона распределения помехового вектор-столбца n с учетом компенсации ковариации помех:
Ковариационная матрица помех

1. Если выборка состоит всего из одного дискрета, корреляционная матрица вырождается: она содержит всего один элемент σ2, а ее определитель |φ| = σ2.
Обратная матрица φ-1 также сводится к одному элементу 1/σ2, а произведение φ·φ-1 – к одноэлементной единичной матрице.
При наличии одной помехи из общего соотношения приходим, таким образом, к выражению wп и wсп , приведенными выше.
2. Получим плотности вероятности Wп(U) и Wсп(U) для случая, когда выборка состоит из двух дискрет.
Корреляционная матрица С в данном случае имеет вид:
Примеры ковариационных матриц

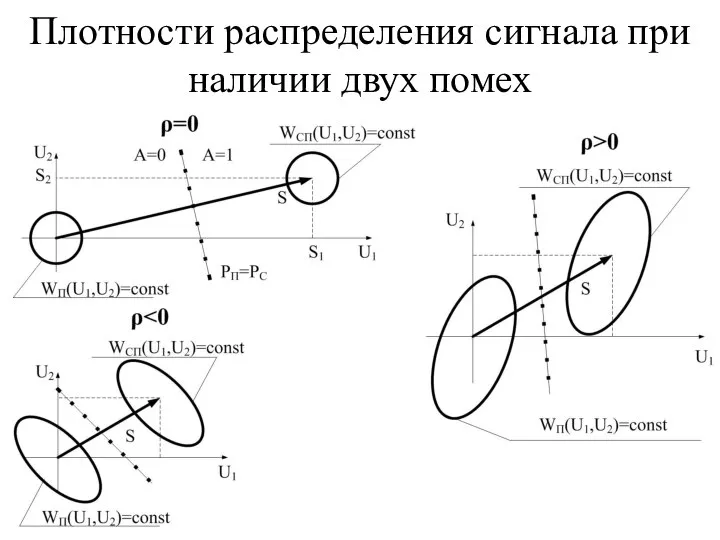
Распределения вероятности в таком случае становятся двумерными и имеют вид
что соответствует записи
Полученные распределения показаны ниже с помощью линий уровня для случаев:
Учет ковариации двух помех

Плотности распределения сигнала при наличии двух помех

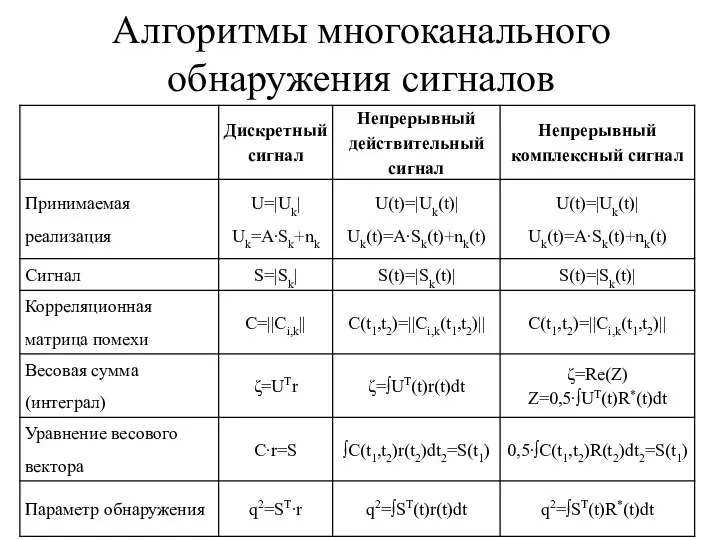
Алгоритмы оптимального многоканального обнаружения
Сводится к сравнению с порогом логарифма отношения правдоподобия, так как логарифм линейное преобразование:
После подстановки плотностей распределения вероятности получим:

С порогом обычно сравнивают:
они монотонно связаны с отношением правдоподобия и каждая из них может использоваться для сравнения с соответствующим порогом при двухальтернативном обнаружении.
Существует несколько вариантов схемы оптимального обнаружителя.
В данном семействе схем подача на элемент схемы скалярной величины показывается с помощью пунктирных стрелок, а векторно-матричной величины с помощью сплошных стрелок стрелок.
Виды схем оптимального многоканального обнаружителя

Проводится два вида обработки m-элементного принятого U:
линейное преобразование U к зависящему только от структуры m2-элементной корреляционной матрицы помехи:
выделение скалярной весовой суммы элементов с весовыми коэффициентами, соответствующими составляющим полезного сигнала и не зависящими от корреляционной матрицы помехи:
Схема 1 оптимального обнаружителя

В данной проводится m-элементная весовая обработка с коэффициентами ri вектора r = ||ri||:
Выходной уровень помехи в схемах 1 и 2 зависит от:
входной корреляционной матрицы С
вектора опорного/зондирующего сигнала S.
Уровень порога ξ0, обеспечивающий заданную условную вероятность ложной тревоги F выбирается с учетом зависимости.
Схема 2 оптимального обнаружителя

Это схема многоканального оптимального обнаружителя с нормированным порогом.
Для оценки отношения правдоподобия здесь в виде весовый коэффициенте используется нормированный вектор r.
Переход к нормированному весовому вектору rн учитывает используемую в радиолокационных приемниках автоматическую регулировку усиления по выходному уровню помехи.
Схема 3 оптимального обнаружителя

Параметр качества двухальтернативного обнаружения
Параметром обнаружения (квадратичным, линейным) называют отношение сигнал-помеха на выходе линейного тракта обработки (по мощности, по напряжению).
Отношение сигнал-помеха по мощности это отношение величины квадрата математического ожидания весовой суммы ξ или ξн при наличии сигнала и помехи к величине дисперсии этой же самой весовой суммы (которая полагается постоянной вне зависимости от наличия или отсутствия сигнала).
Параметры обнаружения приведенных выше оптимальных обнаружителей одинаковы при одинаковых условиях на входе.
Расчет проведем для схемы 1 при наличии сигнала

Если нормировать дисперсию помехи, квадратичный параметр обнаружения будет равен q2, а линейный q.
Для параметра обнаружения справедливы следующие выражения:
Весовая сумма ζн или ζ есть линейная комбинация нормально распределенных величин Ui и за счет закона больших чисел также распределена по нормальному закону.
Так как Mсп{ζн}=q, M{(ζн-q)2}=1, плотности вероятности нормированной весовой суммы имеют вид:
Плотности распределения параметра двухальтернативного обнаружения

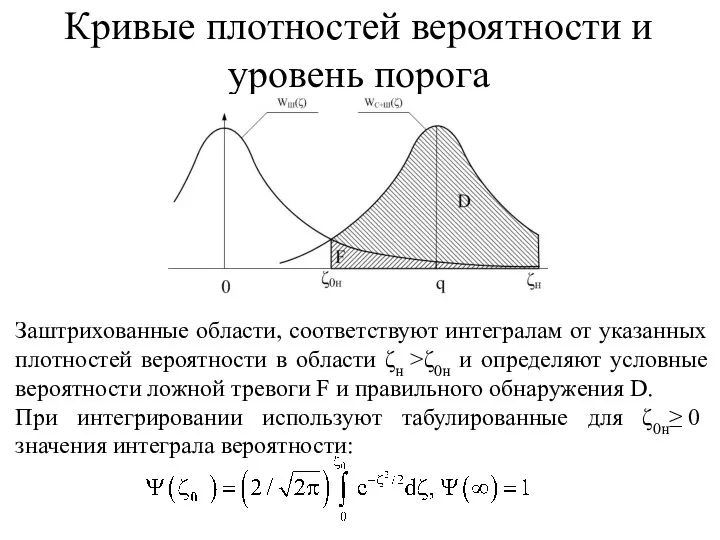
Заштрихованные области, соответствуют интегралам от указанных плотностей вероятности в области ζн >ζ0н и определяют условные вероятности ложной тревоги F и правильного обнаружения D.
При интегрировании используют табулированные для ζ0н≥ 0 значения интеграла вероятности:
Кривые плотностей вероятности и уровень порога

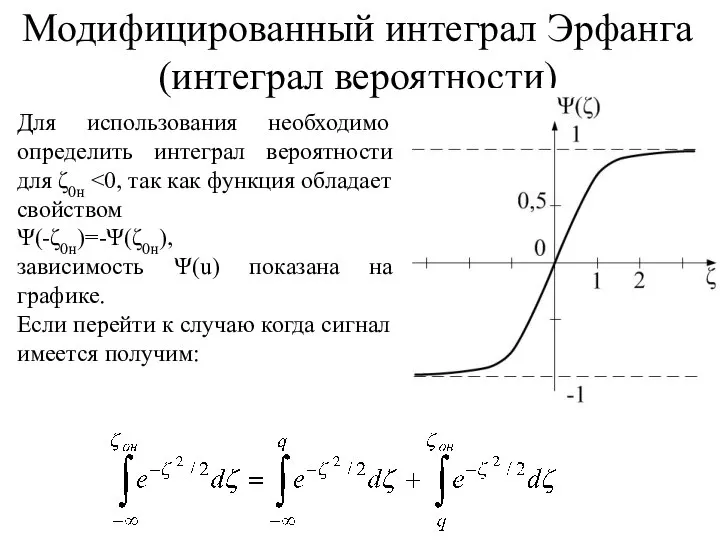
Для использования необходимо определить интеграл вероятности для ζ0н <0, так как функция обладает свойством
Ψ(-ζ0н)=-Ψ(ζ0н),
зависимость Ψ(u) показана на графике.
Если перейти к случаю когда сигнал имеется получим:
Модифицированный интеграл Эрфанга (интеграл вероятности)

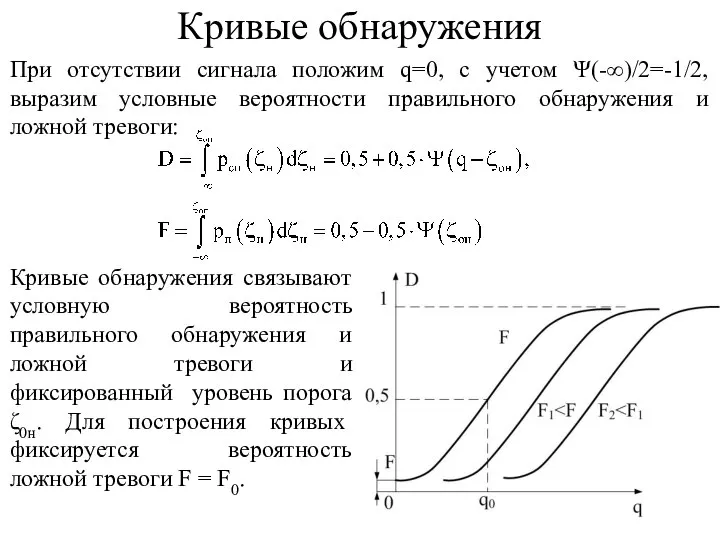
При отсутствии сигнала положим q=0, с учетом Ψ(-∞)/2=-1/2, выразим условные вероятности правильного обнаружения и ложной тревоги:
Кривые обнаружения
Кривые обнаружения связывают условную вероятность правильного обнаружения и ложной тревоги и фиксированный уровень порога ζ0н. Для построения кривых фиксируется вероятность ложной тревоги F = F0.

Условия расчета параметров обнаружения в двухэлементной выборке
При расчете полагают что:
отсутствует корреляция элементов выборки помехи;
помеха стационарна во времени и пространстве;
дисперсия помехи и собственных шумов за время наблюдения постоянна.
Если в выборке имеется более двух элементов данные условия могут быть не выполнены и соответственно требуется информация для декорреляции входной выборки.
Двухэлементная выборка соответствует напряжениям двух элементов антенной системы в один и тот же момент времени. Она образована помехой либо наложением сигнала и помехи. Выборка сигнала S известна. Известна также корреляционная матрица помехи C и обратная ей матрица.

Весовой вектор для структурной схемы 2:
Весовая сумма в таком случае имеет вид
Проведем оптимальное межэлементное взвешивание для устранения не стационарности помехи:
Тогда параметр обнаружения q определяется выражением:
Межэлементное нормирование по уровню помехи

Коэффициент корреляции выборки ρ=0, дисперсии
элементов выборки равны σ12= σ22 =σ2, соответственно:
Каждое из принятых нормированных напряжений U1н, U2н
умножается на соответствующее нормированное по уровню
помехи значение ожидаемого напряжения. Если математическое ожидание ζ в отсутствие сигнала равно нулю Mп{ζн}=0, то при его наличии оно равно:
где |S1н|=q1, |S2н|=q2 – параметры обнаружения элементов выборки. Накопление сигнала осуществляется независимо от знака элементов выборки сигнала с одинаковыми весами элементов выборки, так как дисперсии помехи равны.
Обнаружение и независимые стационарные помехи

1. Коэффициент корреляции выборки ρ=0, дисперсии элементов выборки не равны σ12≠ σ22, соответственно когерентное накопление сигнальных составляющих производится с различными весами:
Весовая обработка связана с межэлементным нормированием принимаемых напряжений по ожидаемому уровню помехи. С меньшим весом учитывается элемент выборки, принимаемый на фоне более интенсивной помехи.
Коэффициент корреляции выборки ρ ≠ 0, дисперсии
элементов выборки не равны σ12≠ σ22, когерентное накопление сигнальных составляющих с учетом когерентной компенсации:
Компенсации коррелированных частей помехи предшествует межэлементное нормирование принимаемых колебаний, обеспечивающее выравнивание помех по интенсивности:
Обнаружение и нестационарные помехи

Для сильно коррелированной помехи роль компенсации может оказаться значительнее роли корреляционного накопления.
Обработка неэффективна, если
т. е. когда отсутствуют существенные различия между сигналом и помехой. В этом случае: q2=q12 и использование второго дискрета не изменяет параметр обнаружения.
Полезный сигнал компенсируется при его использовании вместе с помехой, помеха накапливается, как и полезный сигнал, компенсация, и накопление оказываются неэффективными.
Обнаружение при значительной корреляции помех

Многоканальный корреляционный обнаружитель непрерывного сигнала с известными параметрами на фоне гауссовской коррелированной помехи

Обнаружение непрерывного сигнала
При переходе от дискретных величин к непрерывным выражения для весового интеграла и параметра обнаружения принимают вид:
А для определения весового вектора r(α) необходимо решить интегрально-матричное уравнение:
C(t,α) - матрица взаимных корреляционных функций канальных помеховых напряжений является ядром уравнения;
S(t) – опорный сигнал.
С помощью вектора r(s) можно:
- синтезировать схему обработки, преобразуя rн(s)= r(s)/q можно построить схему обнаружителя с заданной вероятностью ложной тревоги F0;
- определять параметр обнаружения q.

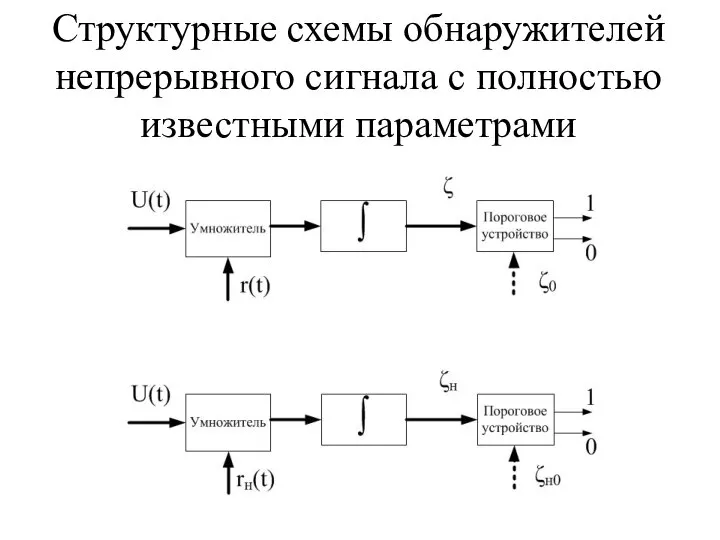
Структурные схемы обнаружителей непрерывного сигнала с полностью известными параметрами

При одноканальном приеме М=1, а помеха - стационарный шумовой процесс с постоянной спектральной плотностью мощности N0 в неограниченной полосе частот (белый шум). По теореме Хинчина корреляционная функция шума с точностью до множителя сводится к дельта-функции:
Подставляя С(t,s)в интегрально-матричное уравнение, получим в силу фильтрующего свойства дельта-функции:
Одноканальное обнаружение непрерывного сигнала

Оптимальная обработка сводится к вычислению и сравнению с порогом нормированного или ненормированного весового интеграла:
Параметр обнаружения q2 сигнала на фоне белого шума равен отношению удвоенной энергии сигнала к спектральной плотности мощности шума:
Выбор порога для одноканального обнаружения

В двух каналах приема (М = 2) действуют некоррелированные стационарные независимые белые шумы со спектральными плотностями N01 и N02. Матрица корреляционных функций имеет вид
Подставляя ее в интегрально-матричное уравнение, получаем следующую систему двух интегральных уравнений:
Независимое двухканальное обнаружение непрерывного сигнала

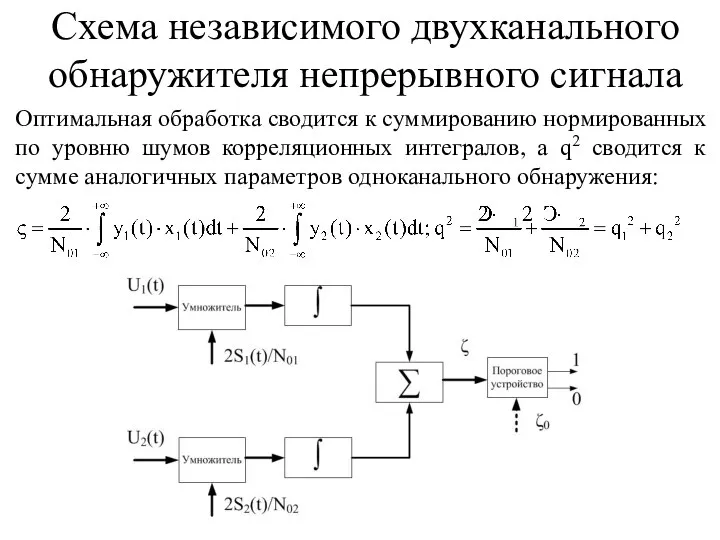
Оптимальная обработка сводится к суммированию нормированных по уровню шумов корреляционных интегралов, а q2 сводится к сумме аналогичных параметров одноканального обнаружения:
Схема независимого двухканального обнаружителя непрерывного сигнала

Каналы с коррелированными помехами встречаются:
- при использовании различных антенных элементов, принимаю­щих колебания общих источников мешающих колебаний;
при использовании незадержанных и задержанных на период посылки мешающих колебаний в импульсном радиолокаторе с селекцией движущихся целей.
Соответственно в каналах имеются коррелированные стационарные помеховые колебания типа белого шума со спектральными плотностями мощности N01 и N02.
Матрица корреляционных функций для рассматриваемых случаев имеет вид
Двухканальное обнаружение при коррелированных помехах

Подставим корреляционную матрицу в интегрально-матричное уравнение, и решим его относительно весового вектора r(t) :
Алгоритм двухканального обнаружения на фоне коррелированных помех

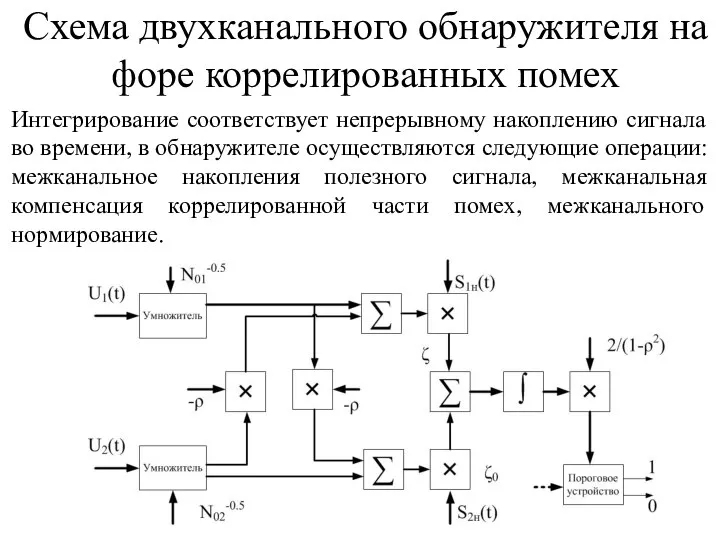
Интегрирование соответствует непрерывному накоплению сигнала во времени, в обнаружителе осуществляются следующие операции: межканальное накопления полезного сигнала, межканальная компенсация коррелированной части помех, межканального нормирование.
Схема двухканального обнаружителя на форе коррелированных помех

Пусть Рассмотрим для одноканального обнаружение воздействие нестационарной дельта-коррелированный шумовой процесс с корреляционной функцией
N0(t) медленно меняющаяся во времени спектральная плотность мощности шума.
Подставим С(t,α) в интегрально-матричное уравнение:
Таким образом алгоритм сводится к взвешиванию временных участков сигнала, меньший вес у участков с большей долей помехи.
Обнаружение на фоне нестационарной помехи

Многоканальный корреляционный обнаружитель комплексного сигнала с полностью известными параметрами

Комплексная модель узкополосного высокочастотного колебания
Полоса узкополосного сигнала значительно меньше несущей частоты f0. С учетом преселекции ограничены полосы помех n(t)=||ni(t)|| и принимаемых колебаний S(t)=||Si(t)||.
Изменение амплитуды ат(t) и начальной фазы φ(t) за период 1/f0 несущей частоты невелики, в пределе их могут полагать постоянными. Воспользовавшись формулами Эйлера после замены переменных получим:

Взаимное влияние пары колебаний
a(t) представляет собой к действительную часть произведения комплексной амплитуды А(t) и высокочастотного комплексного множителя ej· 2π·f0 ·t или к полусумму аналогичных комплексно-сопряженных произведений.
Возьмем другое высокочастотное колебание b(t), взятое в какой-то иной момент времени t2:
Произведение a(t1)·b(t2) сведется к сумме функций разностного и суммарного времен, по формуле Эйлера сведем функции одного времени к реальной части, получим:

Приближенное вычисление интеграла произведения колебаний
При t1 = t2 и медленно изменяющихся A(t) и В(t)
При интегрировании за время t2 - t1, существенно превышающее период колебаний 1/f0, получаем:

Вычисление взаимной корреляционной функции случайных сигналов
Случайными здесь могут быть амплитуды и начальные фазы колебаний a(t1), b(t2), соответственно M[A(t)·B(t)]=0.
M[A(t)·B*(t)] может не быть равным нулю когда A(t) = В(t), а случайные начальные фазы компенсируются, тогда:
Взаимная корреляционная функция С(t1, t2) двух колебаний a(t1) и b(t2) определяется действительной компонентой взаимной корреляционной функции их комплексных амплитуд с учетом высокочастотного множителя.

Комплексная корреляционная матрица помехи
Если принимается сигнал U(t) = ||Ui(t)||, тогда мгновенное значение в соответствующих каналах:
Взаимные корреляционные функции комплексных амплитуд помеховых напряжений в паре каналов имеют вид:
Совокупность этих функций образует комплексную матрицу помеховых взаимных корреляционных функций (комплексную корреляционную матрицу помехи):
U(t)=||Ni(t)||=N(t) – комплексные амплитуды помех.

Комплексная корреляционная матрица помехи С(t1,t2) при t1 = t2 оказывается эрмитовой:
При t1 ≠ t2 справедлива лишь обобщенная эрмитовость комплексной корреляционной матрицы помехи: матрица переходит в комплексно-сопряженную, если вместе с заменой номеров строк и столбцов заменяются аргументы функций:
Весовая интегральная сумма при переходе к комплексной скалярной записи принимает вид
Свойства корреляционной матрицы помехи

Интегрально-матричное уравнение комплексного весового вектора R(t) следует из уравнения вещественного весового вектора r(t) и после преобразования получим:
Выражение параметра обнаружения:
Проведя замены и подставив получим:
Комплексная запись основных соотношений обнаружения

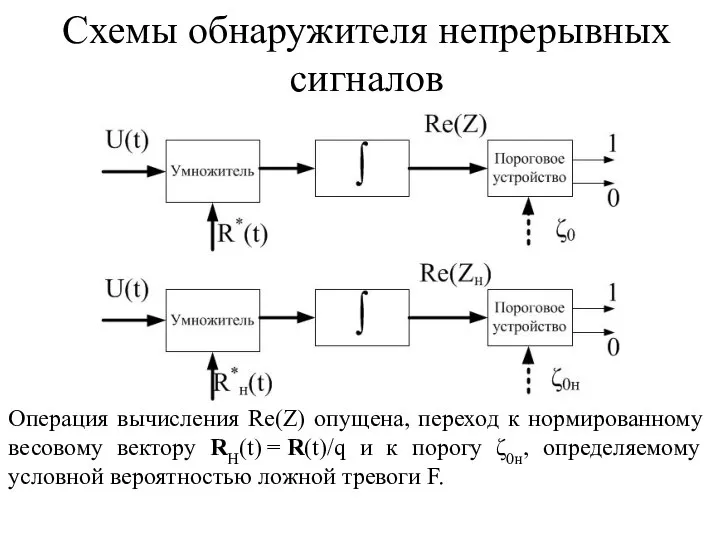
Схемы обнаружителя непрерывных сигналов
Операция вычисления Re(Z) опущена, переход к нормированному весовому вектору RH(t) = R(t)/q и к порогу ζ0н, определяемому условной вероятностью ложной тревоги F.

Алгоритмы многоканального обнаружения сигналов

Модель белого шума для узкополосного сигнала
Действительная корреляционная функция стационарной помехи с равномерно распределенной в полосе Пп спектральной плотностью мощности N0 соответствует выражению
Если полоса помехи больше полосы сигнала функция ∆(τ) переходит в дельта-функцию, тогда:

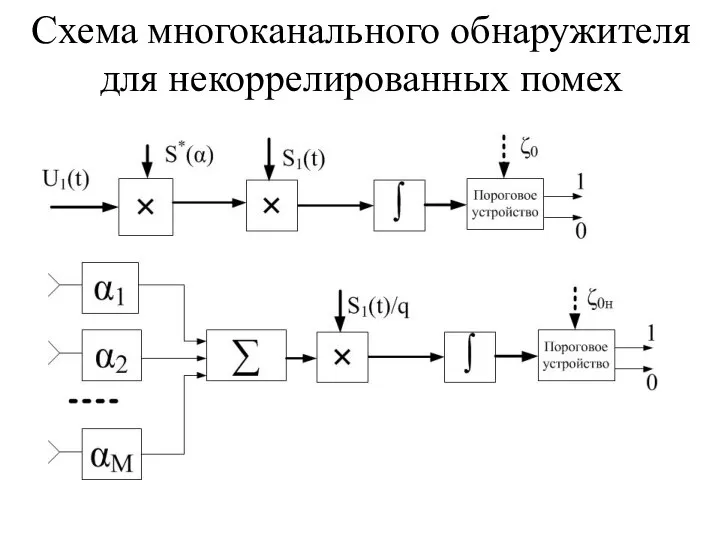
Синтез многоканального обнаружителя для некоррелированных помех
Принимаемый сигнал на антенной решетке:
Вектор α характеризует сдвиги фаз αi (i=1, 2, ..., М), зависящие от угловых координат источника сигнала.
Помеха не коррелирована по времени и элементам разрешения, спектральная плотность мощности постоянная.
Весовой вектор будет иметь вид:
До расчета весового интеграла следует провести пространственную обработку:

Алгоритм обработки сигнала и показатель обнаружения
Алгоритм расчете корреляционного интеграла ζ:
Показатель обнаружения в таком случае:
Алгоритм может использоваться для квадратурного представления сигнала без непосредственного представления сигнала в комплексной форме.

Схема многоканального обнаружителя для некоррелированных помех

Синтез многоканального обнаружителя на фоне коррелированных помех
Комплексная корреляционная матрица помехи
Сигнал имеет вид:
Условия соответствуют приему остронаправленной и слабонаправленной антеннами, соответственно принимаемым слабонаправленной антенной сигналом можно пренебречь. Аналогична ситуация при приеме различных поляризаций.
Система уравнений для комплексных весовых функций: