Содержание
- 2. Список литературы Савельев И.В. Курс общей физики. В 5-и тт. Том 2. Электричество и магнетизм. ISBN
- 3. Основные темы Взаимодействие токов Магнитное поле Закон Био-Савара-Лапласа Поле движущегося заряда Сила Лоренца Закон Ампера Контур
- 4. Взаимодействие токов Опыт показывает, что электрические токи взаимодействуют между собой Два тонких проводника притягиваются друг к
- 5. Взаимодействие токов Коэффициент пропорциональности взят в виде 2k. Закон взаимодействия токов был установлен Ампером в 1820
- 6. Взаимодействие токов В рационализированной форме выражение (6.1) записывается где μ0 – так называемая магнитная постоянная. Значение
- 7. Взаимодействие токов Коэффициент k в формуле (6.1) можно сделать равным 1 за счет выбора единицы силы
- 8. Взаимодействие токов Согласно (6.1) размерность k определяется как Следовательно, в системе СГСЭ k можно представить как
- 9. Взаимодействие токов Вспомним, что 1 Кл=3*109 СГСЭ-ед. заряда 1 дин=10-5 Н, получим подставим значения в (6.1)
- 10. Взаимодействие токов Между электрической постоянной ε0 и магнитной постоянной μ0 имеется связь Найдем размерность и числовое
- 11. Взаимодействие токов Величина произведения ε0 μ0 равна То есть (6.9) (6.10)
- 12. Магнитное поле Взаимодействие токов осуществляется через поле, называемое магнитным Эрстед в 1820 году обнаружил, что при
- 13. Магнитное поле Величину магнитного поля принято обозначать буквой B. Величину B логично называть напряженностью магнитного поля.
- 14. Магнитное поле Опыт показывает, что для магнитного поля справедлив принцип суперпозиции: поле B, порожденное несколькими движущимися
- 15. Магнитное поле Такую нормаль будем называть положительной. Поместив пробный контур в магнитное поле, мы обнаружим, что
- 16. Магнитное поле Модуль момента зависит от угла α между нормалью и направлением поля, достигая наибольшего значения
- 17. Магнитное поле Поскольку контур характеризуется положением в пространстве, магнитный момент следует рассматривать как вектор, направление которого
- 18. Магнитное поле Поэтому в качестве модуля магнитной индукции можно принять величину Mmax – наибольшее значение вращающего
- 19. Закон Био-Савара-Лапласа Био и Савар в 1820 г. провели исследование магнитных полей, создаваемых токами, текущими по
- 20. Закон Био-Савара-Лапласа Для магнитной индукции поля, создаваемого элементом тока длины dl, Лаплас получил формулу Здесь k’
- 21. Закон Био-Савара-Лапласа Коэффициент пропорциональности k’ в формуле (6.15) в СИ равен μ0/4π, μ0 – магнитная пост
- 22. Закон Био-Савара-Лапласа СГСМ-единица магнитной индукции имеет специальное название – гаусс (Гс). К.Ф.Гаусс предложил систему единиц, в
- 23. Закон Био-Савара-Лапласа Формула (6.15) в гауссовой системе имеет вид Модуль выражения (6.16) определяется формулой Где α
- 24. Закон Био-Савара-Лапласа Применим формулу (6.19) для вычисления поля, создаваемого током, текущим по тонкому прямому проводу бесконечной
- 25. Закон Био-Савара-Лапласа Подставим эти выражения в формулу (6.19) Угол α для всех элементов бесконечного прямого тока
- 26. Закон Био-Савара-Лапласа Линии магнитной индукции поля прямого тока представляют собой систему охватывающих провод концентрических окружностей. Рис.4
- 27. Поле движущегося заряда Из формулы (6.16) можно получить выражение для магнитной индукции поля, создаваемого точечным зарядом
- 28. Поле движущегося заряда Учтя, что векторы e’v и dl совпадают по направлению, заменим e’vdl на e’vdl.
- 29. Поле движущегося заряда Здесь r – вектор, проведенный от заряда в точку P поля, r –
- 30. Поле движущегося заряда Появление выделенного направления при движении заряда приводит к тому, что и электрическое поле
- 31. Поле движущегося заряда
- 32. Сила Лоренца На заряд, движущийся в магнитном поле, действует сила, которую мы будем называть магнитной. Опытным
- 33. Сила Лоренца Модуль магнитной силы равен где α - угол между векторами v и B. Из
- 34. Сила Лоренца Поскольку магнитная сила всегда перпендикулярна к скорости заряженной частицы, она не совершает работы над
- 35. Сила Лоренца Пусть заряд q движется со скоростью v параллельно прямому бесконечному проводу, по которому течет
- 36. Сила Лоренца (6.31) Рис.9
- 37. Сила Лоренца Для магнитной силы с учетом (6.24) и (6.27) получается выражение Найдем отношение магнитной силы
- 38. Закон Ампера Если провод, по которому течет ток, помещен в магнитное поле, на каждый из носителей
- 39. Закон Ампера В элементе провода содержится число носителей, равное nSdl (n – число носителей в единице
- 40. Закон Ампера Заменим dV на Sdl и jSdl на jSdl=Idl и получим формулу Эта формула определяет
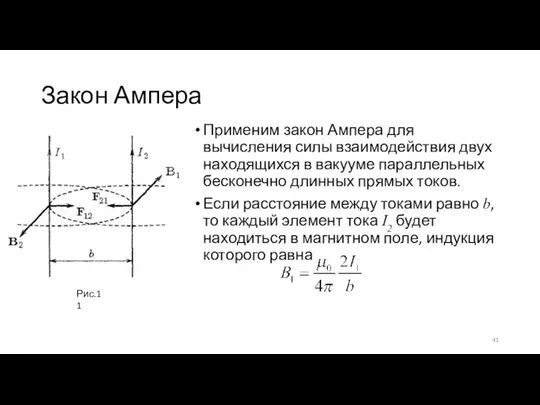
- 41. Закон Ампера Применим закон Ампера для вычисления силы взаимодействия двух находящихся в вакууме параллельных бесконечно длинных
- 42. Закон Ампера Угол α между элементами тока I2 и вектором B1 прямой. Следовательно, согласно (6.39) на
- 43. Контур с током в магнитном поле Выясним, как ведет себя контур с током в магнитном поле.
- 44. Контур с током в магнитном поле Интеграл равен нулю, поэтому и сила F=0 То есть, результирующая
- 45. Контур с током в магнитном поле Вычислим результирующий вращающий момент, созданный силами (6.38), приложенными к контуру.
- 46. Контур с током в магнитном поле Возьмем точку О’, смещенную относительно О на отрезок b. Тогда
- 47. Контур с током в магнитном поле Рассмотрим произвольный плоский контур с током, находящийся в магнитном поле
- 48. Контур с током в магнитном поле На крайний правый элемент контура dl2 действует сила dF2, направленная
- 49. Контур с током в магнитном поле Просуммировав это выражение по все полоскам, получим вращающий момент (здесь
- 50. Контур с током в магнитном поле Аналогом E служит вектор B, а аналогом дипольного электрического момента
- 51. Контур с током в магнитном поле Воспользовавшись обозначением (6.44) можно написать формулу (6.43) следующим образом: Теперь
- 52. Контур с током в магнитном поле Сила, действующая на элемент контура dl, определяется выражением (6.38) Вычислим
- 53. Контур с током в магнитном поле Первый интеграл равен нулю вследствие того, что векторы r и
- 54. Контур с током в магнитном поле Под знаком интеграла стоит полный дифференциал функции r2. Сумма приращений
- 55. Контур с током в магнитном поле Итак, в случае, когда векторы pm и B имеют одинаковое
- 56. Контур с током в магнитном поле Пусть направления векторов pm и B образуют произвольный угол α.
- 57. Контур с током в магнитном поле Из рисунка следует, что Следовательно, в самом общем случае, вращающий
- 58. Контур с током в магнитном поле Для того чтобы угол α между векторами pm и B
- 59. Контур с током в магнитном поле Интегрируя, находим Если положить const=0, форму приобретает вид Параллельная ориентация
- 60. Контур с током в магнитном поле Рис.15
- 61. Контур с током в магнитном поле Поэтому силы, приложенные к элементам контура, образуют симметрический конический веер.
- 62. Контур с током в магнитном поле С помощью выражения (6.49) для энергии контура в магнитном поле
- 63. Контур с током в магнитном поле В этом случае F=Fx и тогда сила будет равна То
- 64. Магнитное поля контура с током Рассмотрим поле, создаваемое током, текущим по тонкому проводу, имеющему форму окружности
- 65. Магнитное поля контура с током Проинтегрируем это выражение по всему контуру: Выражение в скобках равно модулю
- 66. Магнитное поля контура с током Теперь найдем B на оси кругового тока на расстоянии r от
- 67. Магнитное поля контура с током Проинтегрировав по всему контуру и заменив b на получим Эта формула
- 68. Магнитное поля контура с током Выражение (6.54) не зависит от знака r, следовательно в точках оси,
- 69. Магнитное поля контура с током Дополнительные расчеты показывают, что любой системе токов или движущихся зарядов, локализованных
- 70. Магнитное поля контура с током Из всего сказанного вытекает, что дипольный магнитный момент является весьма важной
- 71. Поле соленоида и тороида Соленоид представляет собой провод, навитый на круглый цилиндрический каркас. Линии поля B
- 72. Поле соленоида и тороида Среднее значение этой плотности равно Где n – число витков соленоида, приходящееся
- 73. Поле соленоида и тороида Представим соленоид в виде бесконечного тонкостенного цилиндра, обтекаемого током постоянной линейной плотности
- 74. Поле соленоида и тороида Следовательно, результирующее поле в любой точке внутри и вне бесконечного соленоида может
- 75. Поле соленоида и тороида Чтобы доказать это возьмем внутри соленоида воображаемый прямоугольный контур 1-2-3-4. Обойдя контур
- 76. Поле соленоида и тороида Циркуляция по контуру, изображенному на рисунке, равна a(B+B’). В тоже время циркуляция
- 77. Поле соленоида и тороида Возьмем плоскость, перпендикулярную оси соленоида. Вследствие замкнутости линий B магнитные потоки через
- 78. Поле соленоида и тороида Итак, мы доказали, что вне бесконечно длинного соленоида магнитная индукция равна нулю.
- 79. Поле соленоида и тороида В магнитную индукцию на оси соленоида симметрично расположенные витки вносят одинаковый вклад.
- 80. Поле соленоида и тороида Тороид представляет собой провод, навитый на каркас, имеющий форму тора. Возьмем контур
- 81. Поле соленоида и тороида Если контур проходит внутри тороида, он охватывает ток 2πRnI (R – радиус
- 82. Поле соленоида и тороида В этом случае поле можно считать однородным в каждом из сечений тороида.
- 84. Скачать презентацию
















































































 Обслуживание тормозной системы
Обслуживание тормозной системы Расчет стержневых конструкций по предельному равновесию
Расчет стержневых конструкций по предельному равновесию Широкополосный генератор подавления радиосигналов
Широкополосный генератор подавления радиосигналов Правило Ленца
Правило Ленца Электроемкость. Конденсаторы
Электроемкость. Конденсаторы Порівняння роботи рухомого складу за різними видами тяги
Порівняння роботи рухомого складу за різними видами тяги Презентация на тему Свет и его законы
Презентация на тему Свет и его законы 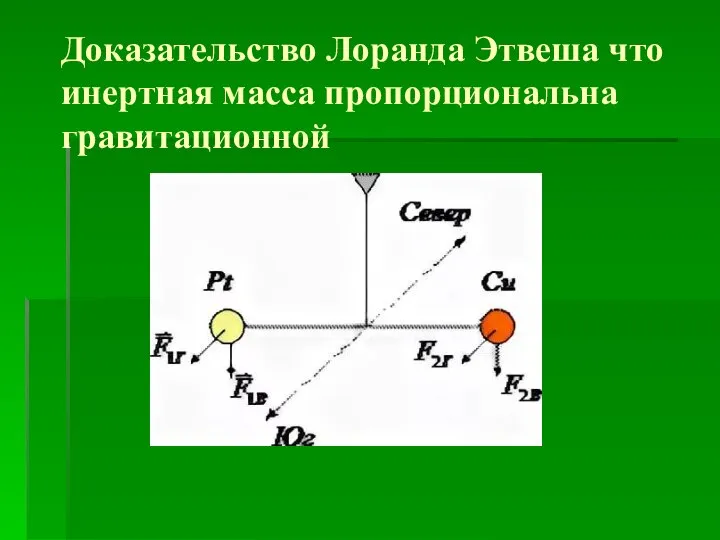 Доказательство Лоранда Этвеша что инертная масса пропорциональна гравитационной
Доказательство Лоранда Этвеша что инертная масса пропорциональна гравитационной Тела,вещества,частицы (1)
Тела,вещества,частицы (1) Развитие интереса к физике у детей начальной школы. Занимательные опыты
Развитие интереса к физике у детей начальной школы. Занимательные опыты Основы динамики
Основы динамики Интерференция и дифракция света
Интерференция и дифракция света Ток в электролитах
Ток в электролитах Политропные процессы. Лабораторная работа
Политропные процессы. Лабораторная работа Работа и мощность
Работа и мощность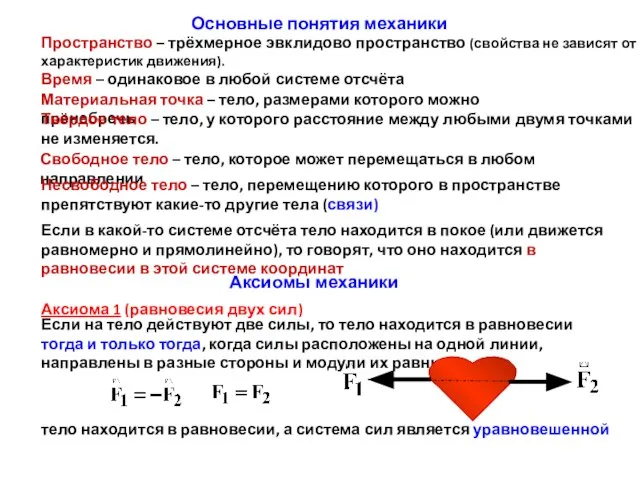 Аксиомы механики
Аксиомы механики Презентация на тему Звуковые волны
Презентация на тему Звуковые волны  Уровнемер для сыпучих материалов
Уровнемер для сыпучих материалов Топология квантовой физики
Топология квантовой физики Презентация на тему Виды сил. Равнодействующая сила. Правила сложения сил
Презентация на тему Виды сил. Равнодействующая сила. Правила сложения сил  Типы астрономических объектов: галактики, звезды, планеты, астероиды, кометы, диффузное вещество
Типы астрономических объектов: галактики, звезды, планеты, астероиды, кометы, диффузное вещество Подшипники качения и скольжения
Подшипники качения и скольжения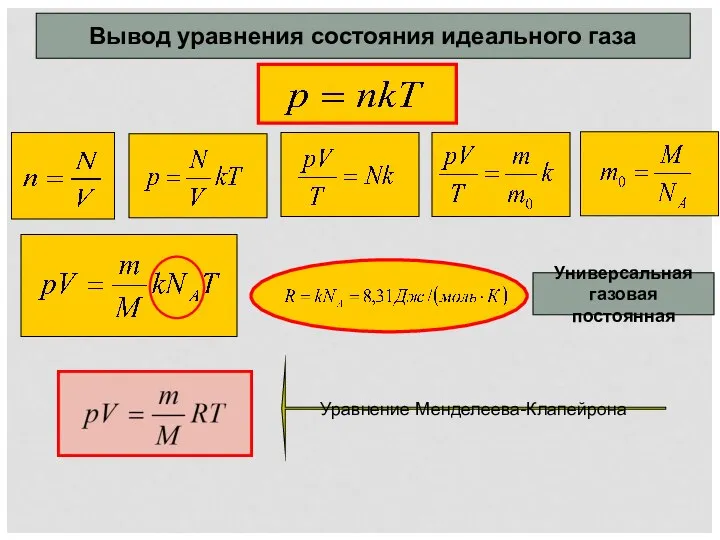 Вывод уравнения Менделеева-Клайперона. Изопроцессы
Вывод уравнения Менделеева-Клайперона. Изопроцессы Сообщающиеся сосуды
Сообщающиеся сосуды Решение задач ЕГЭ на закон Джоуля Ленца
Решение задач ЕГЭ на закон Джоуля Ленца Prezentatsia_7
Prezentatsia_7 Диагностика и ремонт бензонасоса
Диагностика и ремонт бензонасоса Өлшеудің белгісіздігі туралы түсінік
Өлшеудің белгісіздігі туралы түсінік