Слайд 2КРАТКАЯ ТЕОРИЯ
Электроемкостью С любого конденсатора называется физическая
величина, численно равна отношению заряда q

одной из обкладок
Конденсатора к разности потенциалов U между обкладками.
C=q/U
При параллельном соединении конденсаторов их электроемкости складываются.
При последовательном соединении конденсаторов складываются величины, обратные электроемкостям
Слайд 3КРАТКАЯ ТЕОРИЯ
Энергия W заряженного конденсатора в СИ выражается формулами
W=CU²/2 или
W=qU/2

или
W=q²/2C
Слайд 4КРАТКАЯ ТЕОРИЯ
Смешанным соединением конденсаторов называется такое соединение их, при котором имеется

и параллельное и последовательное соединение.
При смешанном соединении конденсаторов для участков с параллельным соединением применяются свойства параллельного соединения конденсаторов, а для участков с последовательным соединением - все свойства последовательного соединения конденсаторов.
Всякое смешанное соединение конденсаторов путем упрощений может быть сведено либо к параллельному соединению, либо к последовательному.
Слайд 6ПРИМЕРЫ РЕШЕНИЯ
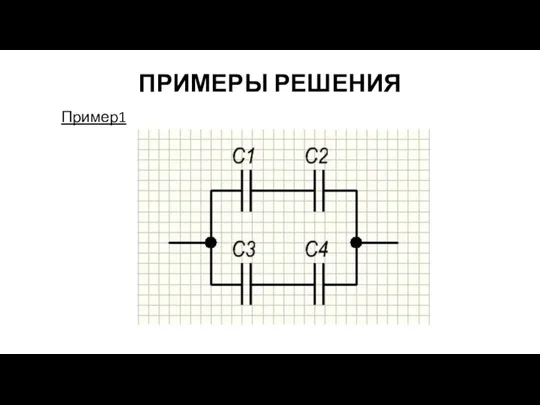
Эквивалентная емкость верхней ветви
Эквивалентная емкость нижней цепи
Теперь это смешанное соединение конденсаторов

может быть приведено к параллельному соединению. Эквивалентная емкость всей батареи конденсаторов
Слайд 8ПРИМЕРЫ РЕШЕНИЯ
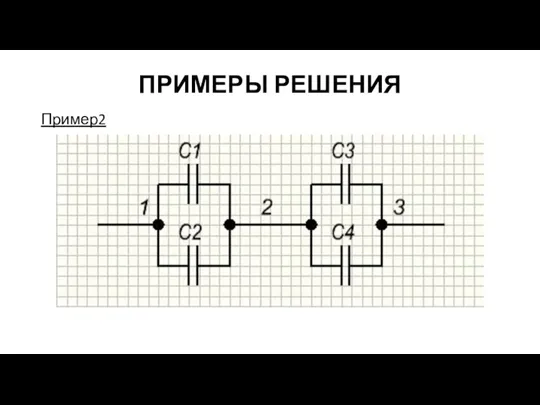
Эквивалентная емкость между точками 1 и 2:
С1,2=С1+С2
Эквивалентная емкость между точками

2 и 3
С3,4=С3+С4
Теперь это смешанное соединение конденсаторов может быть приведено к последовательному соединению
Слайд 9ПРИМЕРЫ РЕШЕНИЯ
Эквивалентная емкость батареи конденсаторов

Слайд 10ПРИМЕРЫ РЕШЕНИЯ
Пример 3
Конденсатор емкостью С=2 мкф и номинальным рабочим напряжением Up=600 в

вышел из строя.
Составить схему замены его конденсаторами емкостью С=1 мкф и номинальным рабочим напряжением Up=200 в
Слайд 11ПРИМЕРЫ РЕШЕНИЯ
Р е ш е н и е .Конденсаторы с номинальным рабочим

напряжением 200 в нельзя включать под напряжение 600в. Поэтому прежде всего необходимо обеспечить электрическую прочность батареи. Для этого конденсаторы надо соединить последовательно. Число последовательно соединенных конденсаторов должно быть
Емкость такой ветви
Слайд 12ПРИМЕРЫ РЕШЕНИЯ
Для обеспечения емкости батареи необходимо соединить несколько параллельных ветвей. Число параллельных

ветвей
Слайд 13ПРИМЕРЫ РЕШЕНИЯ
Общая схема замены конденсатора

Слайд 14ПРИМЕРЫ РЕШЕНИЯ
К какой паре точек схемы, изображенной на рис., надо подключить источник

тока, чтобы зарядить все шесть конденсаторов, емкости которых равны?
Слайд 15ПРИМЕРЫ РЕШЕНИЯ
Решение: Нетрудно понять, что схема, предложенная в задаче, представляет собой «правильный»

тетраэдр, в ребра которого «включены» шесть одинаковых конденсаторов. Поэтому из соображений симметрии ясно, что, к какой бы паре точек мы ни подключили источник, всегда найдется конденсатор, который не будет заряжен (конденсатор ребра, скрещенного с ребром подключения источника). Например, на рис. при подключении источника к точкам А и В конденсатор, соединяющий точки С и D, не будет заряжен, поскольку потенциалы точек С и D равны.
Слайд 16ПРИМЕРЫ РЕШЕНИЯ
Определить ёмкость получившейся батареи конденсаторов, если включить такой куб в цепь
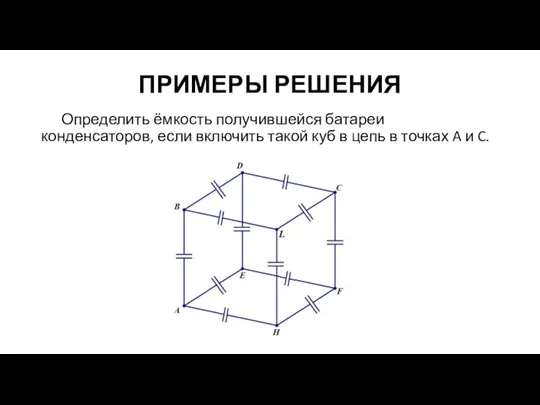
в точках A и C.
Слайд 17ПРИМЕРЫ РЕШЕНИЯ
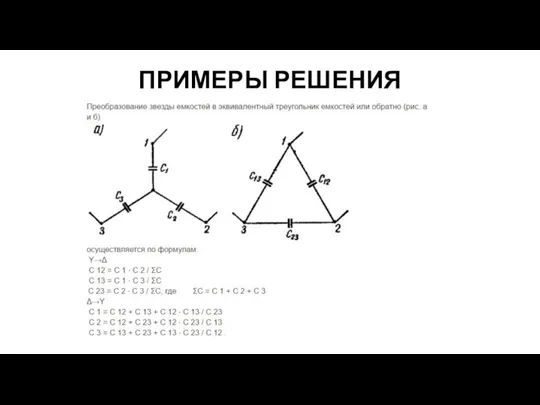
Шаг 1. Сначала пересчитаем звезды из емкостей BDCE, BLCH и EFHC

в треугольники
Слайд 18ПРИМЕРЫ РЕШЕНИЯ
Результат пересчета звезды BDCE с геометрических позиций таков:

Слайд 20ПРИМЕРЫ РЕШЕНИЯ
Тогда для нашего случая:
Аналогично будут пересчитаны и две другие звезды

Слайд 21ПРИМЕРЫ РЕШЕНИЯ
Шаг 2. Видим, что между точками B и C включены параллельно

две емкости (красное и голубое ребро), аналогично – две такие же емкости включены между точками E и C – красное и зеленое ребра, и между точками H и C – зеленое и голубое ребра. Так как параллельно соединенные емкости складываются, то преобразуем пары этих ребер в единичные, сложив их емкости:
Слайд 22ПРИМЕРЫ РЕШЕНИЯ
Образовались рыжие ребра с емкостями по 2C\3.

Слайд 23ПРИМЕРЫ РЕШЕНИЯ
Шаг 3. Посмотрим теперь на схему: видно, что потенциалы точек B,

E, H равны. Таким образом, емкости, оказавшиеся включенными в голубое, красное и зеленое ребра окажутся незаряженными. Поэтому просто исключим их из схемы, получив при этом очень простую конструкцию:
Слайд 24ПРИМЕРЫ РЕШЕНИЯ
Рассчитаем емкость ребра ABC:
Так как ребра ABC, AEC и AHC включены

параллельно, их емкости можно сложить:
Ответ:




















 Явление электромагнитной индукции
Явление электромагнитной индукции Силы в природе. 10 класс
Силы в природе. 10 класс Альтернативные источники энергии
Альтернативные источники энергии Потери электроэнергии в электрических сетях
Потери электроэнергии в электрических сетях Типовой расчет ТР2-ОС
Типовой расчет ТР2-ОС Презентация на тему Явление электромагнитной индукции
Презентация на тему Явление электромагнитной индукции  Атомная энергетика. Общие сведения
Атомная энергетика. Общие сведения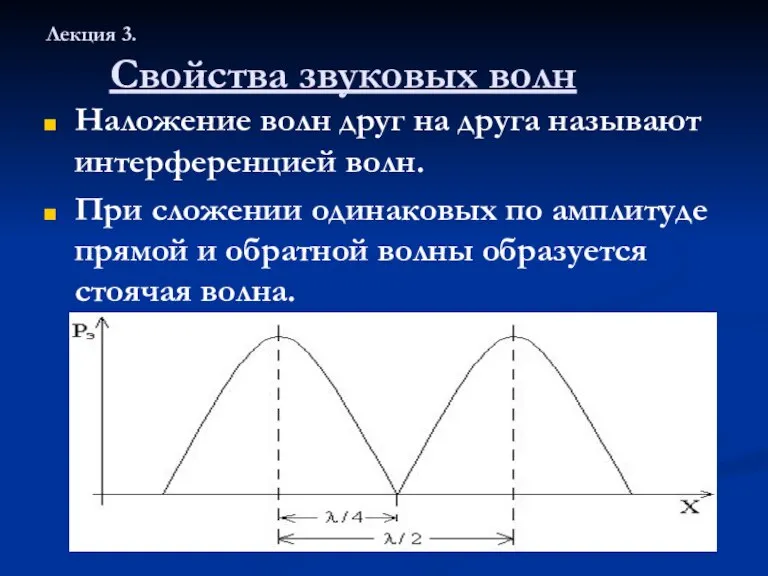 Свойства звуковых волн
Свойства звуковых волн Бесциркуляционное течение около цилиндра. Лекция 7
Бесциркуляционное течение около цилиндра. Лекция 7 Определение объёма твердого тела
Определение объёма твердого тела Преломление света
Преломление света Физический океан
Физический океан Физический маятник
Физический маятник Семинар по физике для 83 и 84 групп
Семинар по физике для 83 и 84 групп Диэлектриктер физикасы
Диэлектриктер физикасы Развитие двигателя внутреннего сгорания
Развитие двигателя внутреннего сгорания Газовые законы
Газовые законы Работа совершаемая при термодинамических процессах. Количество теплоты. Теплоемкость
Работа совершаемая при термодинамических процессах. Количество теплоты. Теплоемкость Презентация по физике "В мире электромагнетизма" -
Презентация по физике "В мире электромагнетизма" -  Состояние мотивационной сферы дошкольника с НОДА (ДЦП)
Состояние мотивационной сферы дошкольника с НОДА (ДЦП) Принципы действия тепловых двигателей
Принципы действия тепловых двигателей Проставка на раму
Проставка на раму Энергия связи ядра. Ядерные реакции
Энергия связи ядра. Ядерные реакции Решение задач: Гидродинамика. Ламинарное и турбулентное течения жидкостей и газов
Решение задач: Гидродинамика. Ламинарное и турбулентное течения жидкостей и газов Тезаурус. Реактор. Генератор
Тезаурус. Реактор. Генератор Радиоизотопное излучение
Радиоизотопное излучение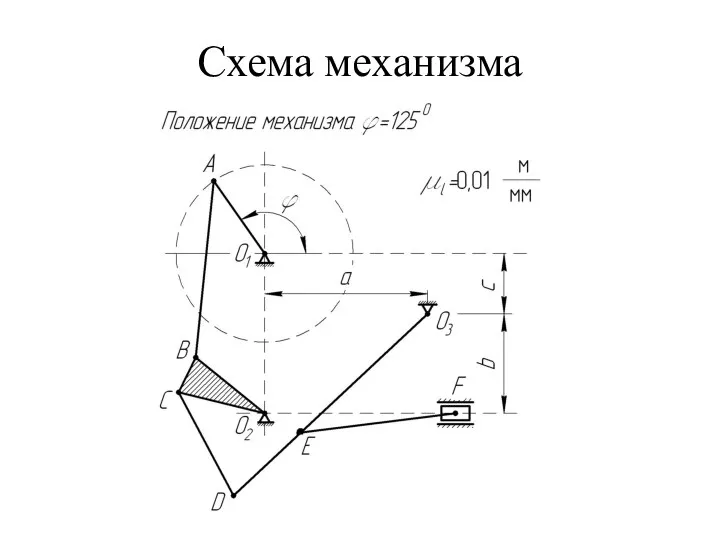 Схема механизма. Пример оформления работы
Схема механизма. Пример оформления работы Постоянный электрический ток и его законы
Постоянный электрический ток и его законы