Магнитное_поле_в_веществе

Список литературы
Савельев И.В. Курс общей физики. В 5-и тт. Том 2. Электричество и магнетизм. ISBN - 978-5-8114-1208-2. Издательство «Лань». 2021 г.
Савельев И.В. Курс общей физики. В 5-и тт. Том 4. Волны. Оптика. ISBN - 978-5-8114-1210-5. Издательство «Лань». 2021 г.
Трофимова Т. И. Руководство к решению задач по физике : учебное пособие для прикладного бакалавриата: Учебное пособие/Трофимова Т. И..-М:Издательство Юрайт,2019, ISBN 978-5-9916-3429-8.-265. https://elis.psu.ru/node/557918

Основные темы
Циркуляция и ротор векторного поля
Дивергенция и ротор магнитного поля
Намагничение магнетика
Напряженность магнитного поля
Вычисление поля в магнетиках
Условия на границе двух магнетиков
Виды магнетиков
Магнитомеханические явления
Диамагнетизм
Парамагнетизм
Ферромагнетизм

Циркуляция векторного поля
Представим себе канал очень тонкого сечения, в котором течет жидкость.
Этот канал включает в себя контур Г.
В зависимости от характера поля вектора скорости v жидкость в канале будет либо неподвижной, либо будет циркулировать в том или ином направлении.
Циркуляцией вектора v по контуру Г называют величину, равную произведению скорости жидкости в канале на длину канала.
Циркуляция любого вектора a по произвольному замкнутому контуру Г
Рис.1

Ротор векторного поля
Циркуляция C вектора a состоит из суммы циркуляций элементарных площадок ΔS.
Элементарная циркуляция ΔC зависит не от длины контура, а от поверхности элементарной площадки, охватываемой контуром.
То есть, циркуляция порождается на поверхности.
Плотность порождения циркуляции это циркуляция, порождаемая бесконечно малым участком поверхности в расчете на единицу площади этого участка:
Рис.2

Ротор векторного поля
Этот вектор называют ротором векторного поля и обозначают символом rot a либо [∇a]
В однородном поле циркуляция по любому контуру равна нулю.
Плотность порождения циркуляции так же равна нулю.
В неоднородном поле плотность порождения циркуляции ведет себя при вращении контура как проекция вектора er на нормаль к контуру
Рис.3

Ротор векторного поля
Плотность порождения циркуляции равна проекции характеризующего поле вектора rot a на положительную нормаль к контуру
Наглядное представление о роторе v можно получить, представив небольшую крыльчатку, помещенную в жидкость.
В тех местах, где ротор отличен от нуля, крыльчатка будет вращаться, причем с тем большей скоростью, чем больше проекция ротора на ось крыльчатки.
Рис.4

Теорема Стокса
Зная ротор вектора a в каждой точке некоторой поверхности, можно вычислить циркуляцию этого вектора по контуру Г.
Теорема Стокса гласит, что циркуляция вектора a по произвольному контуру Г равна потоку вектора rot a через произвольную поверхность S, ограниченную данным контуром Г.
То есть, ротор соотносится с циркуляцией подобно тому как дивергенция соотносится с потоком.
Дивергенция порождает поток.
Ротор порождает циркуляцию.

Дивергенция и ротор магнитного поля
Отсутствие в природе магнитных зарядов приводит к тому, что линии вектора B магнитной индукции не имеют ни начала ни конца.
Поэтому поток вектора B через замкнутую поверхность должен быть равен нулю.
Таким образом, для любого магнитного поля и произвольной замкнутой поверхности S имеет место условие
Заменив поверхностный интеграл на объемный получим, что
(7.1)

Дивергенция и ротор магнитного поля
Это условие должно выполняться для любого произвольного объема V.
Это возможно, если подынтегральная функция в каждой точке поля равна нулю.
Таким образом, магнитное поле обладает тем свойством, что его дивергенция всюду равна нулю:
Циркуляция вектора B по определению равна
Ротор вектора магнитной индукции пропорционален вектору плотности тока в данной точке
(7.2)
(7.3)
(7.4)

Дивергенция и ротор магнитного поля
Дивергенция E равна ρ, деленному на ε0
Дивергенция B равна 0
Ротор E равен 0
Ротор B равен j, умноженному на μ0
Сопоставление этих формул показывает, что электростатическое и магнитное поля имеют существенно различный характер.

Намагничение магнетика
Если несущие ток провода находятся не в вакууме, а в какой либо среде, магнитное поле изменяется.
Это объясняется тем, что всякое вещество является магнетиком, т.е. способно под действием магнитного поля приобретать магнитный момент (намагничиваться).
Намагниченное вещество создает магнитное поле B’, которое накладывается на обусловленное токами поле B0.
Оба поля в сумме дают результирующее поле
(7.5)

Намагничение магнетика
Истинное (микроскопическое) поле в магнетике сильно изменяется в пределах межмолекулярных расстояний.
Под B подразумевается усредненное (макроскопическое) поле.
Для объяснения намагничения Ампер предположил, что в молекулах вещества циркулируют круговые токи (молекулярные токи).
Каждый такой ток обладает магнитным моментом и создает в окружающем пространстве магнитное поле.
В отсутствие внешнего поля молекулярные токи ориентированы хаотично, вследствие чего результирующее поле равно нулю.

Намагничение магнетика
В силу хаотичной ориентации магнитных моментов молекул суммарный магнитный момент тела также равен нулю.
Под действием поля магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении, вследствие чего магнетик намагничивается – его суммарный магнитный момент становится отличным от нуля.
Магнитные поля отдельных молекулярных токов в этом случае уже не компенсируют друг друга и возникает поле B’.

Намагничение магнетика
Намагничение магнетика естественно характеризовать магнитным моментом единицы объема.
Эту величину называют намагниченностью и обозначают буквой J.
Если магнетик намагничен неоднородно, намагниченность в данной точке определяется следующим выражением
Где ΔV – физически бесконечно малый объем, взятый в окрестности рассматриваемой точки, pm – магнитный момент отдельной молекулы, заключенной в объеме ΔV.
(7.6)

Намагничение магнетика
Поле B’, так же как и поле B0, не имеет источников. Поэтому дивергенция результирующего поля (7.1) равна нулю:
Таким образом, для магнитного поля в веществе справедливы выражения
(7.7)
(7.8)

Напряженность магнитного поля
Напишем выражение для ротора результирующего поля (7.5):
Ранее мы показывали, что
Где j – плотность макроскопического тока.
Аналогично ротор вектора B’ должен быть пропорционален плотности молекулярных токов:
Следовательно, ротор результирующего поля определяется как
(7.9)

Напряженность магнитного поля
Для того, чтобы определить ротор B, нужно знать плотность не только макроскопических, но также и молекулярных токов.
Плотность же токов, зависит от значения вектора B.
Для того, чтобы выйти из ситуации можно найти вспомогательную величину, ротор которой определяется только плотностью макроскопических зарядов.
Чтобы установить вид этой вспомогательной величины, попробуем выразить плотность молекулярных токов jмол через намагниченность магнетика J.

Напряженность магнитного поля
Для чего вычислим алгебраическую сумму молекулярных токов jмол, охватываемых некоторым контуром Г. Эта сумма равна
где S – поверхность, натянутая на контур.
В алгебраическую сумму молекулярных токов входят только те токи, которые оказываются «нанизанными» на контур (I’мол)
(7.10)
Токи не «нанизанные» на контур, либо не пересекут поверхность, либо пересекут ее дважды, один раз в одном направлении, второй раз - в другом (I’’мол).
Рис.5

Напряженность магнитного поля
В результате их вклад в алгебраическую сумму токов, охватываемых контуром, оказывается равным нулю.
Из рисунка видно, что элемент контура dl, образующий с направлением намагниченности J угол α, нанизывает на себя те молекулярные токи, центры которых попадают внутрь косого цилиндра с объемом Sмолcosα dl
(Sмол – площадь, охватываемая отдельным молекулярным током).
Если n – число молекул в единице объема, то суммарный ток, охватываемый элементом dl, равен IмолnSмолcosα dl.
Произведение IмолSмол равно магнитному моменту pm отдельного молекулярного тока.
Рис.6

Напряженность магнитного поля
Следовательно выражение IмолSмолn представляет собой магнитный момент единицы объема, т.е. дает модуль вектора j, а IмолnSмолcosα dl – проекцию вектора J на направление элемента dl.
Таким образом суммарный молекулярный ток, охватываемый элементом dl, равен Jdl, а сумма молекулярных токов, охватываемых всем контуром, равна
Преобразовав правую часть по теореме Стокса, получим

Напряженность магнитного поля
Это равенство должно выполняться при произвольном выборе поверхности S.
Это возможно лишь в том случае, если подынтегральные выражения равны в каждой точке магнетика:
Таким образом, плотность молекулярных токов определяется значением ротора намагниченности.
В случае, когда ротор намагниченности [∇J] равен нулю, молекулярные токи отдельных молекул ориентированы так, что их сумма в среднем равна нулю.
(7.11)

Напряженность магнитного поля
Формула (7.6) допускает следующую наглядную интерпретацию.
На рисунке 7 изображены векторы намагниченности J1 и J2 в непосредственной близости к точке P.
Точка P и оба вектора лежат в плоскости рисунка.
Изображенный штриховой линией контур Г также расположен в плоскости рисунка.
Если характер намагниченности таков, что векторы J1 и J2 одинаковы по модулю, то циркуляция J по контуру Г будет равна нулю.
Соответственно [∇J] в точке P также будет равен нулю.
Рис.7

Напряженность магнитного поля
Намагниченностям J1 и J2 можно сопоставить молекулярные токи i’1 и i’2, текущие по контурам, изображенным на рисунке сплошными линиями.
Эти контуры лежат в плоскости, перпендикулярной к плоскости рисунка.
При одинаковом направлении векторов J1 и J2 направления токов i’1 и i’2 в точке P будут взаимно противоположными.
В силу J1=J2 токи i’1 и i’2 одинаковы по величине, вследствие чего результирующий молекулярный ток в точке P оказывается, как и [∇J], равным нулю: jмол=0.
Рис.7

Напряженность магнитного поля
Теперь допустим, J1>J2. Тогда циркуляция J по контуру Г окажется отличной от нуля.
Соответственно поле вектора J в точке P будет характеризоваться вектором [∇J], направленным за чертеж.
Большей намагниченности отвечает больший молекулярный ток, поэтому i’1>i’2.
В итоге в точке P будет наблюдаться отличный от нуля результирующий ток, характеризуемый плотностью jмол, направленной так же как и ∇J, за чертеж.
В случае J1

Напряженность магнитного поля
Итак, в точках, где отличен от нуля ротор намагниченности, оказывается отличной от нуля и плотность молекулярных токов, причем векторы [∇J] и jмол имеют одинаковое направление.
Подставим выражение (7.11) для плотности молекулярных токов в формулу (7.9)
Разделив это выражение на μ0 и объединив роторы, получим
(7.12)

Напряженность магнитного поля
Из выражения (7.12) следует, что искомая величина, ротор которой определяется одними лишь макроскопическими токами, равна:
Эта величина называется напряженностью магнитного поля.
В соответствии с (7.12) ротор вектора H равен вектору плотности макроскопических токов:
(7.13)
(7.14)

Напряженность магнитного поля
Возьмем произвольный контур Г с натянутой на него поверхностью S и образуем выражение
Согласно теореме Стокса левая часть этого равенства эквивалентна циркуляции вектора H по контуру Г, следовательно
(7.15)

Напряженность магнитного поля
Если макроскопические токи текут по проводам, охватываемым контуром, соотношение (7.15) можно записать в виде
Формулы (7.15) и (7.16) выражают теорему о циркуляции вектора H:
циркуляция вектора напряженности магнитного поля по некоторому контуру равна алгебраической сумме макроскопических токов, охватываемых этим контуром.
(7.16)

Напряженность магнитного поля
Напряженность магнитного поля H является аналогом электрического смещения D.
Первоначально предполагалось, что в природе существуют подобные электрическим зарядам магнитные массы.
Именно тогда были введены понятия магнитная индукция для B и напряженность поля для H.
Впоследствии выяснилось, что магнитных масс в природе не существует и что величина, названная магнитной индукцией B, в действительности является аналогом не электрического смещения D, а напряженности электрического поля E.
Соответственно H – аналог D, а не E.

Напряженность магнитного поля
Однако изменять уже установившуюся терминологию не стали.
К тому же, вследствие различной природы электрического и магнитного полей (электрическое поле потенциально, а магнитное поле соленоидально) величины B и D обнаруживают много сходства в своем поведении.
Например, линии B как и D не претерпевают разрыва на границе двух сред.

Напряженность магнитного поля
Напряженность поля прямого тока в вакууме определяется как
Из чего следует, что напряженность магнитного поля имеет размерность силы тока, деленную на размерность длины.
В СИ единица напряженности магнитного поля носит название ампер на метр (А/м).
В гауссовой системе напряженностью магнитного поля называют величину
Из этого следует, что в вакууме H совпадает с B. Единица H в гауссовой системе называемая эрстедом (Э), имеет ту же величину и размерность что и гаусс (Гс).
(7.17)
(7.18)

Напряженность магнитного поля
Намагниченность принято связывать не с магнитной индукцией, а с напряженностью поля.
Полагают, что в каждой точке магнетика
Где (кси) – характерная для данного магнетика величина, называемая магнитной восприимчивостью.
является безразмерной величиной.
(7.19)

Напряженность магнитного поля
Подставив в формулу (7.13) выражение (7.19) для J, получим
Безразмерная величина
называется относительной магнитной проницаемостью, или просто магнитной проницаемостью.
Магнитная восприимчивость может быть как положительной, так и отрицательной.
Поэтому магнитная проницаемость μ может быть как больше, так и меньше единицы
(7.20)
(7.21)

Напряженность магнитного поля
С учетом (7.21) формуле (7.20) можно придать вид
В гауссовой системе
Поэтому магнитной проницаемостью вещества называется безразмерная величина
(7.22)
(7.23)
(7.24)

Напряженность магнитного поля
То есть (7.23) можно выразить как
Значение μ в гауссовой системе совпадает со значением μ в СИ.
Из этого следует, что
(7.25)
(7.26)

Вычисление поля в магнетиках
Рассмотрим поле, создаваемое бесконечно длинным круглым намагниченным стержнем.
Намагниченность J будем считать всюду одинаковой и направленной по оси стержня.
Разобьем мысленно стержень на перпендикулярные к оси слои толщиной dl.
Каждый слой разобьем в свою очередь на малые цилиндрические элементы с основаниями произвольной площади.
Каждый такой элемент обладает магнитным моментом
(7.27)
Рис.8

Вычисление поля в магнетиках
Поле B’, создаваемое элементом на расстояниях, больших по сравнению с его размерами, эквивалентно полю, которое создавал бы ток силы I=Jdl, обтекающий элемент по его боковой поверхности.
Действительно, магнитный момент такого тока равен
На больших расстояниях магнитное поле определяется только модулем и направлением магнитного момента.
Воображаемые токи, текущие по общему для двух соседних элементов участку поверхности, одинаковы по величине и противоположны по направлению, поэтому сумма их равна нулю.
Таким образом, некомпенсированными останутся только токи, текущие по боковой поверхности.

Вычисление поля в магнетиках
Из этого следует, что слой стержня толщины dl создает поле, эквивалентное полю, которое создавал бы ток силы Jdl, обтекающий слой по боковой поверхности.
Линейная плотность этого тока равна jлин=J
Весь же бесконечный намагниченный стержень создает поле, эквивалентное полю цилиндра, обтекаемого током с линейной плотностью jлин=J.
Ранее мы выяснили, что вне такого цилиндра поле равно нулю, а внутри цилиндра поле однородно и равно
(7.28)

Вычисление поля в магнетиках
Пусть имеется однородное поле B0, создаваемое макротоками в вакууме.
Согласно (7.22) напряженность этого поля равна
Внесем в это поле (будем называть его внешним) бесконечно длинный круглый стержень из однородного и изотропного магнетика, расположив его вдоль направления B0.
Из соображений симметрии следует, что возникающая в стержне намагниченность J коллинеарна с вектором B0.
(7.29)

Вычисление поля в магнетиках
Намагниченный стержень создает внутри себя поле B’, определяемое (7.28).
В результате поле внутри стержня станет равным
Подставив это значение B в формулу (7.13), получим напряженность поля внутри стержня
Таким образом, напряженность поля в стержне оказывается совпадающей с напряженностью внешнего поля.
(7.30)

Вычисление поля в магнетиках
Умножив H на μ0μ, получим магнитную индукцию внутри стержня:
Отсюда следует, что магнитная проницаемость μ показывает, во сколько раз усиливается поле в магнетике.
Заметим, что поскольку поле B’ отлично от нуля только внутри стержня, магнитное поле вне стержня остается без изменений.
Полученный результат бывает справедлив в тех случаях, когда однородный и изотропный магнетик заполняет объем, ограниченный поверхностями, которые образованы линиями напряженности внешнего поля.
В противном случае напряженность поля не совпадает с H0=B0/μ0
(7.31)

Вычисление поля в магнетиках
Условно полагают, что напряженность поля в магнетике равна
где H0 – внешнее поле, а H> - так называемое размагничивающее поле, которое предполагается пропорциональным намагниченности:
Коэффициент пропорциональности N называется размагничивающим фактором.
Он зависит от формы магнетика.
Для тела, поверхность которого не пересекается линиями напряженности внешнего поля, размагничивающий фактор равен нулю.
(7.32)
(7.33)

Вычисление поля в магнетиках
Для тонкого диска, перпендикулярного внешнему полю, N=1, а для шара N=1/3.
Соответствующий расчет показывает, что если однородный и изотропный магнетик имеющий форму эллипсоида, помещается в однородное внешнее поле, магнитное поле хотя и отлично в нем, но тоже однородно.
То же справедливо для шара (частный случай эллипсоида), а также для длинного стержня, и тонкого диска, которые можно считать предельными случаями эллипсоида.

Вычисление поля в магнетиках
В заключении найдем поле бесконечно длинного соленоида, заполненного однородным и изотропным магнетиком.
Применив к соленоиду теорему о циркуляции (7.16), получим соотношение Ha=naI, отсюда
Таким образом, напряженность поле внутри бесконечного соленоида равно произведению силы тока на число витков, приходящееся на единицу длины.
Вне соленоида поле равно нулю.
(7.34)

Условия на границе двух магнетиков
Вблизи поверхности раздела двух магнетиков векторы B и H должны удовлетворять определенным граничным условиям, которые вытекают из соотношений (см. Формулы 7.2 и 7.9)
Мы рассматриваем стационарные поля
Возьмем на границе двух магнетиков с проницаемостями μ1 и μ2 воображаемую цилиндрическую поверхность высоты h с основаниями S1 и S2, расположенными по разные стороны поверхности раздела.
(7.35)

Условия на границе двух магнетиков
Поток вектора B через эту поверхность равен
В соответствии с тем, что ∇B=0, поток вектора B через любую замкнутую поверхность равен нулю.
(7.36)
Приравняв нулю выражение (7.36) и сделав переход h →0, придем к соотношению B1n=-B2n
Если проецировать B1 и B2 на одну и ту же нормаль, получится условие
(7.37)
Рис.9

Условия на границе двух магнетиков
Используем выражение (7.22) и получим
Из чего следует, что
(7.38)
Теперь возьмем на границе магнетиков прямоугольный контур и вычислим для него циркуляцию H.
При малых размерах контура циркуляцию можно представить в виде
(7.39)
Где - среднее значение Hl на перпендикулярных к границе участках контура.
Рис.9

Условия на границе двух магнетиков
Если по границе раздела не текут макроскопические токи, [∇H] в пределах контура будет равен нулю.
Поэтому и циркуляция будет равна нулю.
Положив выражение (7.39) равным нулю и осуществив предельный переход b →0 придем к соотношению
Заменим составляющие H на составляющие вектора B, деленными на μ0μ и получим соотношение
(7.40)
из которого следует
(7.41)

Условия на границе двух магнетиков
На рисунке показано поведение линий B при пересечении границы раздела двух магнетиков.
По аналогии с выражением (7.41) можем получить закон преломления линий магнитной индукции
(7.42)
При переходе в магнетик с большей μ линии магнитной индукции отклоняются от нормали к поверхности.
Это приводит к сгущению линий.
Рис.10

Условия на границе двух магнетиков
Сгущение линий B в веществе с большой магнитной проницаемостью дает возможность формировать магнитные пучки, т.е. придавать им необходимую форму и направление.
Для того, чтобы осуществить магнитную защиту некоторого объема, его окружают железным экраном.
Сгущение линий в толщине экрана приводит к ослаблению поля внутри.
Рис.11

Условия на границе двух магнетиков
На рисунке схема лабораторного электромагнита
От состоит из железного сердечника, на который насажены питаемые током катушки.
Линии магнитного поля сосредоточены в основном внутри сердечника.
Лишь в узком воздушном зазоре они проходят в среде с малой μ.
Вектор B пересекает границы между воздушным зазором и сердечником по нормали к поверхности раздела.
Отсюда согласно (7.37) следует что магнитная индукция в зазоре и в сердечнике одинакова по модулю.
Рис.12

Условия на границе двух магнетиков
Применим теорему о циркуляции H к контуру, проходящему через ось сердечника.
Напряженность поля можно считать всюду в железе одинаковой и равной Hжел=B/(μ0μжел).
Напряженность поля в воздухе будет Hвозд=B/(μ0μвозд)
Обозначим длину участка контура в железе через lжел, а в зазоре – lвозд.
Тогда циркуляцию можно представить в виде Hжел lжел +Hвозд lвозд
Эта циркуляция должна быть равна NI, где N – суммарное количество витков, а I – сила тока.

Условия на границе двух магнетиков
Таким образом получим
Отсюда, с учетом того, что μвозд отличается от единицы лишь в пятом знаке после запятой, получим
Обычно lвозд бывает порядка 0,1 м, lжел – порядка 1 м, μжел достигает значений порядка нескольких тысяч, поэтому вторым слагаемым в знаменателе можно пренебречь и тогда получим
(7.43)

Условия на границе двух магнетиков
Следовательно, магнитная индукция в зазоре электромагнита имеет такое же числовое значение, какое она имела бы внутри тороида без сердечника, на единицу длины которого было бы намотано число витков, равное N/lвозд.
Увеличивая общее число витков и уменьшая размеры воздушного зазора, можно получать поля с большим значением B.
Практически с помощью электромагнитов с железным сердечником удается получать поля с B порядка нескольких тесла.

Виды магнетиков
Формула (7.19) определяет магнитную восприимчивость единицы объема вещества.
Часто вместо этой восприимчивости пользуются отнесенной к одному молю вещества молярной восприимчивостью
Очевидно, что , где Vм – объем моля вещества.
В то время как - безразмерная величина, измеряется в м3/моль.
В зависимости от знака и величины магнитной восприимчивости все магнетики разделяются на три группы

Виды магнетиков
Кроме того, в отличие от диа- и парамагнетиков, для которых не зависит от H, восприимчивость ферромагнетиков является функцией напряженности магнитного поля.
Таким образом, намагниченность J может как совпадать по направлению с H (у пара- и ферромагнетиков), так и быть направленной в противоположную сторону (у диамагнетиков).

Диамагнетизм
Электрон, движущийся по орбите, подобен волчку, поэтому ему должны быть свойственны все особенности гироскопов под действием внешних сил.
Отношение магнитного момента элементарной частицы к ее механическому моменту называется магнитомеханическим (или гиромагнитным) соотношением
При соответствующих условиях должна возникать прецессия электронной орбиты
Условия прецессии возникают, если атом находится в магнитном поле B.
В этом случае на орбиту действует вращающий момент N=[pmB], стремящийся установить орбитальный магнитный момент электрона pm по направлению поля.
(7.44)

Диамагнетизм
При этом механический момент M установится против поля
Под действием момента N векторы pm и М совершают прецессию вокруг направления вектора магнитной индукции B.
Найдем скорость этой прецессии.
За время dt вектор M получает приращение dM, равное
Вектор dM, как и вектор N, перпендикулярен к плоскости, проходящей через векторы B и M; его модуль равен
Где α - угол между pm и B.
Рис.13

Диамагнетизм
За время dt плоскость, в которой лежит вектор M, повернется вокруг направления B на угол
Разделив этот угол на dt, получим угловую скорость прецессии:
Из чего следует
Где e – заряд электрона, а m – масса электрона
(7.45)
Рис.13

Диамагнетизм
Частоту (7.45) называют частотой ларморовой прецессии или просто ларморовой частотой.
Она не зависит ни от угла наклона орбиты по отношению к направлению магнитного поля, ни от радиуса орбиты или скорости электрона.
Следовательно, ларморова частота одинакова для всех электронов, входящих в состав атома.
Прецессия орбиты обусловливает дополнительное движение электрона вокруг направления поля.

Диамагнетизм
Если бы расстояние r’ электрона от параллельной B оси, проходящей через центр орбиты, не изменялось, дополнительное движение электрона происходило по окружности радиуса r’.
Ему соответствовал бы круговой ток I’=e(ωL/2π) вокруг заштрихованной площади S, магнитный момент которого направлен в сторону, противоположную B
(7.46)
Этот момент называется индуцированным или наведенным магнитным моментом

Диамагнетизм
В действительности, вследствие движения электрона по орбите, расстояние r’ все время изменяется.
Поэтому в формуле (7.46) вместо r’2нужно брать усредненное по времени значение 〈 r’2 〉.
Это среднее значение зависит от угла α, характеризующего ориентацию плоскости орбиты по отношению к B.
В частности, для орбиты, перпендикулярной к вектору B, r’ постоянно и равно радиусу орбиты r.
Для орбиты, плоскость которой проходит через направление B, r’ изменяется по закону r’=rsinωt, где ω - угловая скорость обращения электрона по орбите.

Диамагнетизм
Следовательно
Если произвести усреднение по всем возможным значениям α, считая их равновероятными, то получается
Подставив в (7.46) значение (7.45) и (7.47), получим для среднего значения индуцированного магнитного момента электрона следующее выражение
Знак минус отражает то обстоятельство, что векторы 〈 p’m 〉 и B направлены в противоположные стороны.
(7.47)
(7.48)

Диамагнетизм
В общем случае (например для эллиптической орбиты) вместо r2 нужно взять 〈 r2〉, то есть средний квадрат расстояния электрона от ядра.
Просуммировав выражение (7.48) по всем электронам, найдем индуцированный момент атома:
(Z – атомный номер химического элемента, число электронов в атоме равно Z).
Итак, под действием внешнего магнитного поля происходит прецессия электронных орбит с одинаковой для всех электронов угловой скоростью.
(7.49)

Диамагнетизм
Обусловленное прецессией дополнительное движение электронов приводит к возникновению индуцированного магнитного момента атома, направленного против поля.
Ларморова прецессия возникает у всех без исключения веществ.
Однако в тех случаях, когда атомы обладают сами по себе магнитным моментом, магнитное поле не только индуцирует момент (7.49), но и оказывает на магнитные моменты атомов ориентирующее воздействие, устанавливая их по направлению поля.

Диамагнетизм
Возникающий при этом положительный магнитный момент бывает значительно больше, чем отрицательный индуцированный момент.
Поэтому результирующий момент оказывается положительным и вещество ведет себя как парамагнетик.
Диамагнетизм обнаруживают только те вещества, у которых атомы не обладают собственным магнитным моментом

Парамагнетизм
Если магнитный момент pm атомов отличен от нуля, вещество ведет оказывается парамагнитным.
Магнитное поле стремится установить магнитные моменты атомов вдоль B, а тепловое движение стремится разбросать их по всем направлениям.
В результате устанавливается некоторая преимущественная ориентация моментов вдоль поля, тем большая чем больше B, и тем меньшая, чем выше температура.
П.Кюри экспериментально установил закон, согласно которому магнитная восприимчивость парамагнитного вещества равна
Где C – постоянная Кюри, зависящая от рода вещества, а Т – термодинамическая температура
(7.50)

Парамагнетизм
Классическая теория парамагнетизма была развита Ланжевеном в 1905 году.
Для не слишком сильных полей и не очень низких температур значение магнитной восприимчивости для парамагнетиков равно
Где NA – постоянная Авогардо, а k – постоянная Больцмана.
(7.51)
(7.52)
И следовательно, значение постоянной Кюри

Парамагнетизм
В очень сильных полях и при низких температурах наблюдается отступления от пропорциональности между намагниченностью парамагнетика J и напряженностью поля H
В частности, может наступить магнитное насыщение, при котором все pm выстраиваются по полю и дальнейшее увеличение H не приводит к возрастанию J.

Ферромагнетизм
Особый класс магнетиков образуют вещества, способные обладать намагниченностью в отсутствие внешнего магнитного поля.
По своему наиболее распространенному представителю – железу – они получили название ферромагнетиков.
К их числу, кроме железа, принадлежат никель, кобальт, гадолиний, их сплавы и соединения, а также некоторые сплавы и соединения марганца и хрома с неферромагнитными элементами.
Ферромагнетизм присущ всем этим веществам только в кристаллическом состоянии.

Ферромагнетизм
Ферромагнетики являются сильномагнитными веществами.
Их намагниченность в огромное (до 1010) число раз превосходит намагниченность диа- и парамагнетиков, принадлежащих к категории слабомагнитных веществ.
Намагниченность слабомагнитных веществ изменяется линейно.
Намагниченность ферромагнетиков зависит от H сложным образом.
На рисунке 14 показана кривая намагничения ферромагнетика, магнитный момент которого первоначально был равен нулю.
Она называется основной или нулевой кривой намагничения.
Рис.14

Ферромагнетизм
Уже в полях порядка нескольких эрстед (~100А/м) намагниченность J достигает насыщения.
Основная кривая намагничения на диаграмме B-H приведена на рисунке 15 (кривая 0-1).
Напомним, что B=μ0(H+J). Поэтому по достижении насыщения B продолжает расти с H по линейному закону:
Кривая намагничения железа была впервые получена и подробно исследована Столетовым.
Рис.15

Ферромагнетизм
Кроме нелинейной зависимости между H и J (или между H и B), для ферромагнетиков характерно также наличие гистерезиса.
Если довести намагничивание до насыщения (точка 1) и затем уменьшать напряженность магнитного поля, то индукция B следует не по первоначальной кривой 0-1, а изменяется в соответствии с кривой 1-2.
В результате, когда напряженность внешнего поля станет равной нулю, (точка 2), намагничение не исчезает и характеризуется величиной Br, которая называется остаточной индукцией.
Намагниченность при этом имеет значение Jr, называемое остаточной намагниченностью.
Рис.15

Ферромагнетизм
Индукция B обращается в нуль лишь под действием поля Hc, имеющего направление, противоположное полю, вызвавшему намагничение.
Напряженность Hc называется коэрцитивной силой.
Существование остаточной намагниченности делает возможным изготовление постоянных магнитов.
Постоянный магнит тем лучше сохраняет свои свойства, чем больше коэрцитивная сила материала, из которого он изготовлен.
Рис.15

Ферромагнетизм
При действии на ферромагнетик переменного магнитного поля индукция изменяется в соответствии с кривой 1-2-3-4-5-1, которая называется петлей гистерезиса.
Аналогичная петля получается и на диаграмме J-H
Если максимальные значения H таковы, что намагниченность достигает насыщения, получается так называемая максимальная петля гистерезиса.
Если при амплитудных значениях H насыщение не достигается, получается петля, называемая частным циклом.
Частных циклов бесконечное множество, все они лежат внутри максимальной петли гистерезиса.
Рис.15

Ферромагнетизм
Гистерезис приводит к тому, что намагничение ферромагнетика не является однозначной функцией H.
Оно в сильной мере зависит от предыстории образца – от того, в каких полях он побывал прежде.
В связи с неоднозначностью зависимости B от H понятие магнитной проницаемости применяется лишь к основной кривой намагничения.
Магнитная проницаемость ферромагнетиков μ (а следовательно, и магнитная восприимчивость ) является функцией напряженности поля.

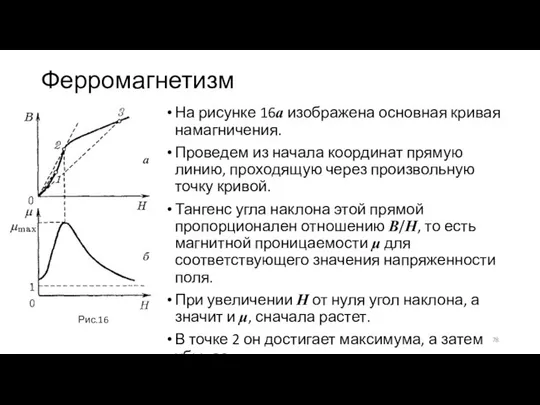
Ферромагнетизм
На рисунке 16а изображена основная кривая намагничения.
Проведем из начала координат прямую линию, проходящую через произвольную точку кривой.
Тангенс угла наклона этой прямой пропорционален отношению B/H, то есть магнитной проницаемости μ для соответствующего значения напряженности поля.
При увеличении H от нуля угол наклона, а значит и μ, сначала растет.
В точке 2 он достигает максимума, а затем убывает.
Рис.16

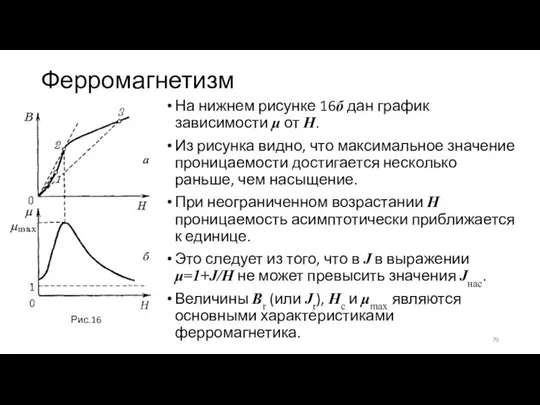
Ферромагнетизм
На нижнем рисунке 16б дан график зависимости μ от H.
Из рисунка видно, что максимальное значение проницаемости достигается несколько раньше, чем насыщение.
При неограниченном возрастании H проницаемость асимптотически приближается к единице.
Это следует из того, что в J в выражении μ=1+J/H не может превысить значения Jнас.
Величины Br (или Jr), Hc и μmax являются основными характеристиками ферромагнетика.
Рис.16

Ферромагнетизм
Если коэрцитивная сила Hc велика, ферромагнетик называется жестким.
Для него характерна широкая петля гистерезиса.
Ферромагнетик с малой Hc и соответственно узкой петлей гистерезиса называется мягким.
В зависимости от назначения берутся ферромагнетики с той или иной характеристикой.
Для постоянных магнитов используются жесткие ферромагнетики.
Для сердечников трансформаторов – мягкие.

Ферромагнетизм

Ферромагнетизм
Из опытов по изучению магнитомеханических явлений следует, что ответственными за магнитные свойства ферромагнетиков являются собственные (спиновые) магнитные моменты электронов.
При определенных условиях могут возникать силы, которые заставляют магнитные моменты электронов выстраиваться параллельно друг другу.
В результате возникают области спонтанного намагничения, которые называют доменами.
В пределах каждого домена ферромагнетик намагничен до насыщения и обладает определенным магнитным моментом.

Ферромагнетизм
Направления этих моментов для разных доменов различны, так что в отсутствии внешнего поля суммарный момент всего тела равен нулю.
Домены имеют размеры порядка 1-10 мкм.
Действие поля на домены на разных стадиях процесса намагничения оказывается различным.
Вначале, при слабых полях, наблюдается смещение границ доменов, в результате чего происходит увеличение тех доменов, моменты которых составляют с H меньший угол, за счет доменов, у которых угол между векторами pm и H больше.
Домены 1 и 3 увеличиваются за счет доменов 2 и 4.
Рис.17

Ферромагнетизм
С увеличением напряженности поля этот процесс идет все дальше и дальше, пока домены с меньшими углами не поглотят целиком энергетически менее выгодные домены.
На следующей стадии имеет место поворот магнитных доменов в направлении поля.
При этом моменты электронов в пределах домена поворачиваются одновременно, без нарушения строгой параллельности друг другу.
Эти процессы являются необратимыми, что и служит причиной гистерезиса.

Ферромагнетизм
Для каждого ферромагнетика имеется определенная температура Tc, при которой области спонтанного намагничения распадаются и вещество утрачивает свойство ферромагнетика.
Эта температура называется точкой Кюри.
Для железа она равна 768°С, а для Никеля 365 °С.
При температуре выше точки Кюри ферромагнетик становится обычным парамагнетиком, магнитная восприимчивость которого подчиняется закону Кюри-Вейсса
(7.53)

Ферромагнетизм
При охлаждении ферромагнетика ниже точки Кюри в нем снова возникают домены.
В некоторых случаях обменные силы приводят к возникновению так называемых антиферромагнетиков (хром, марганец и др.).
В антиферромагнетиках собственные магнитные моменты электронов самопроизвольно ориентированы антипараллельно друг другу.
Такая ориентация охватывает попарно соседние атомы.
В результате антиферромагнетики обладают крайне малой магнитной восприимчивостью и ведут себя как очень слабые парамагнетики.