Механическое движение

Совокупность неподвижных друг относительно друга тел, по отношению к которым рассматривается движение, и отсчитывающих время часов называется системой отсчета
Линия, которую описывает материальная точка при своем движении, называется траекторией. В зависимости от формы траектории различают прямо-
линейное движение, движение по окружности, криволинейное движение и т. д.
Отрезок прямой, проведенный из начального положения частицы в конечное, называется перемещением. На рис. 1.1.1 вектор перемещения
Рис. 1.1.1
радиус вектор - орты декартовой системы координат
Рис. 1.1.2

§ 1.2. Скорость и ускорение точки
Скорость — это векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчета.
Рис. 1.2.1
Средняя скорость
Скорость точки
Рис. 1.2.2
(1.2.1)
вектор скорости точки в данный момент равен производной, от радиуса-вектора точки по времени и направлен по касательной к траектории движения точки

радиус вектор - орты декартовой системы координат
Согласно (1.2.1)
Скорость в декартовой системе координат
(1.2.2)
(1.2.3)
Из (1.2.2) и (1.2.3) следует
(1.2.4)
Компоненты скорости равны производным соответствующих координат по времени
Вектор ускорения точка равен первой производной от скорости или второй производной от радиуса-вектора точки по времени.

Компоненты ускорения равны вторым производным соответствующих координат по времени
Представим скорость в виде
(1.2.5)
- орт вектора
Рассмотрим два частных случая: 1) движение по прямолинейной траектории и 2) равномерное движение по окружности
1. При прямолинейном движении
2. При равномерном движении по окружности
, поэтому
Из рис. 1.2.3 следует, что за время
орт скорости поворачивается на угол
и получает приращение
(1.2.6)
(1.2.7)

Рис. 1.2.3

Рис. 1.2.4

Глава 2. Простейшие движения твердого тела
2.1. Поступательное движение твердого тела.
Поступательным движением тела называется такое движение, при котором любая прямая, проведённая в теле, всё время перемещается параллельно своему первоначальному положению (рис. 2.1.1).
Рис. 2.1.1
Проведем радиусы векторы к точкам А и В
Тогда,
При поступательном движении все точки твердого тела имеют в любой момент времени одинаковые скорости и ускорения.
Для описания поступательного движения твердого тела достаточно знать, как движется одна из его точек. Все остальные точки движутся таким же образом.

2.2. Вращательное движение твердого тела (ТТ).
При вращательном движении ТТ все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.
Положение тела определяется углом поворота
вокруг оси относительно какого-либо заранее выбранного положения. Этот угол измеряется в радианах. Чтобы определить положение тела в любой момент времени, должен быть задан угол поворота как функция времени (t), рис. 2.2.1 .
Эта функция называется уравнением вращения тела.
Векторы, направления которых связываются с направлением вращения, называются псевдовекторами.
Рис. 2.2.1
Элементарные повороты тела можно рассматривать как векторы . Модуль вектора равен углу поворота, а его направление совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, т.е. подчиняется правилу правого винта.
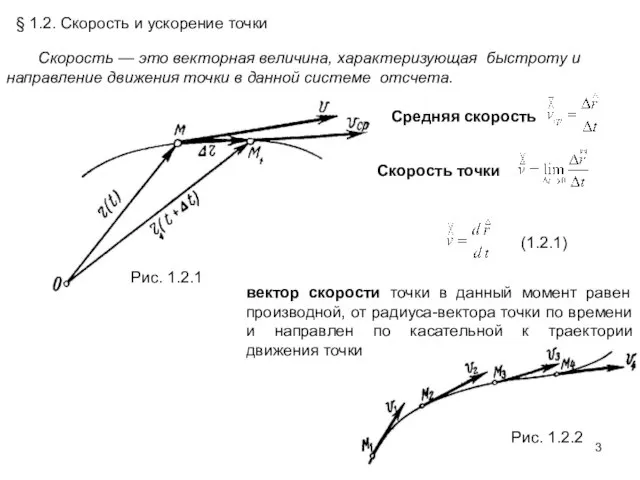
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени

Рис. 2.2.2