Механические передачи. Цилиндрические и конические зубчатые передачи. (Лекция 5)

Конструктивные особенности и параметры ЦКЗП.
В зубчатых колесах можно выявить 4 основных элемента:
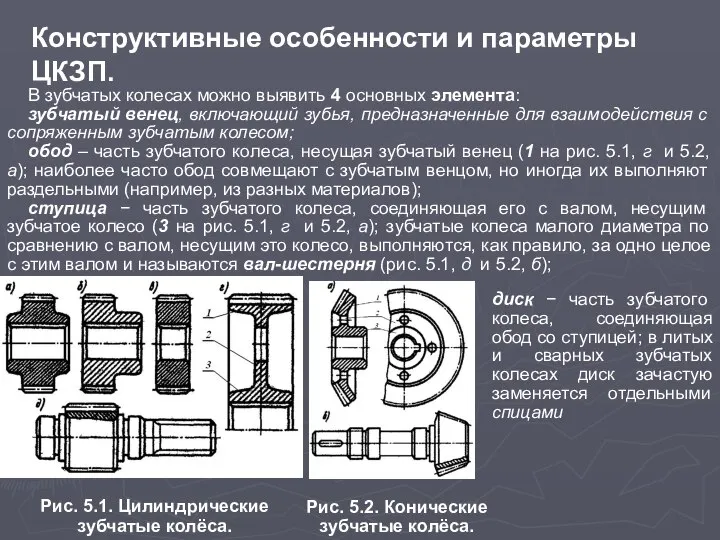
зубчатый венец, включающий зубья, предназначенные для взаимодействия с сопряженным зубчатым колесом;
обод – часть зубчатого колеса, несущая зубчатый венец (1 на рис. 5.1, г и 5.2, а); наиболее часто обод совмещают с зубчатым венцом, но иногда их выполняют раздельными (например, из разных материалов);
ступица − часть зубчатого колеса, соединяющая его с валом, несущим зубчатое колесо (3 на рис. 5.1, г и 5.2, а); зубчатые колеса малого диаметра по сравнению с валом, несущим это колесо, выполняются, как правило, за одно целое с этим валом и называются вал-шестерня (рис. 5.1, д и 5.2, б);
.
Рис. 5.1. Цилиндрические зубчатые колёса.
Рис. 5.2. Конические
зубчатые колёса.
диск − часть зубчатого колеса, соединяющая обод со ступицей; в литых и сварных зубчатых колесах диск зачастую заменяется отдельными спицами

Рис. 5.3. Конструктивные параметры
точеных и кованых колес.
Конструктивные параметры зубчатых колес представлены на рис. 5.3. Толщина обода цилиндрических и конических зубчатых колес может быть выбрана по соотношению
, (5.1)
в котором m – модуль зацепления (для конических колес следует использовать внешний модуль me (mte)), b – ширина зубчатого венца.
Толщину диска принимают равной:
для цилиндрических колёс , (5.2)
для конических колёс . (5.3)
Диаметр ступицы - dст = 1,55d, а её длину − lст = (0,8…1,5)d, где d – посадочный диаметр вала.
У колес большого диаметра с целью экономии легированной стали иногда применяют насадной зубчатый венец (сборные зубчатые колёса), который крепится на ободе так, чтобы исключить возможность его проворачивания.

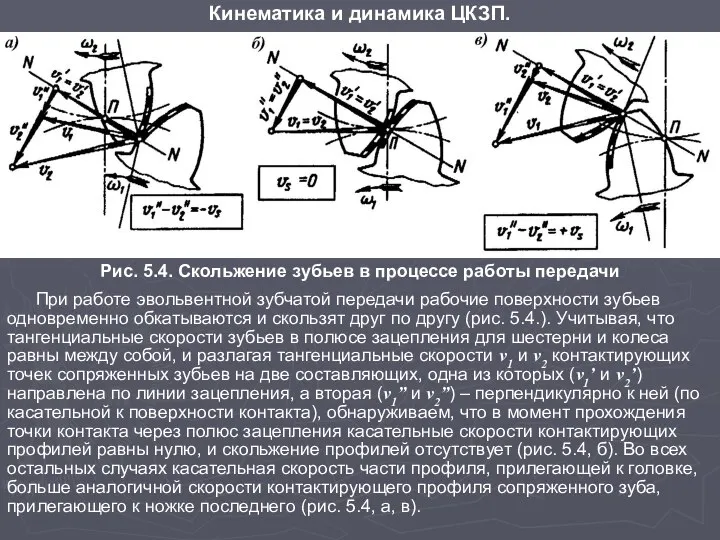
Рис. 5.4. Скольжение зубьев в процессе работы передачи
При работе эвольвентной зубчатой передачи рабочие поверхности зубьев одновременно обкатываются и скользят друг по другу (рис. 5.4.). Учитывая, что тангенциальные скорости зубьев в полюсе зацепления для шестерни и колеса равны между собой, и разлагая тангенциальные скорости v1 и v2 контактирующих точек сопряженных зубьев на две составляющих, одна из которых (v1’ и v2’) направлена по линии зацепления, а вторая (v1” и v2”) – перпендикулярно к ней (по касательной к поверхности контакта), обнаруживаем, что в момент прохождения точки контакта через полюс зацепления касательные скорости контактирующих профилей равны нулю, и скольжение профилей отсутствует (рис. 5.4, б). Во всех остальных случаях касательная скорость части профиля, прилегающей к головке, больше аналогичной скорости контактирующего профиля сопряженного зуба, прилегающего к ножке последнего (рис. 5.4, а, в).

Поскольку протяженность профилей ножки и головки примерно одинаковы, ножка зуба работает в наиболее неблагоприятных условиях (дольше работает в условиях трения скольжения), что ведет к её более интенсивному изнашиванию.
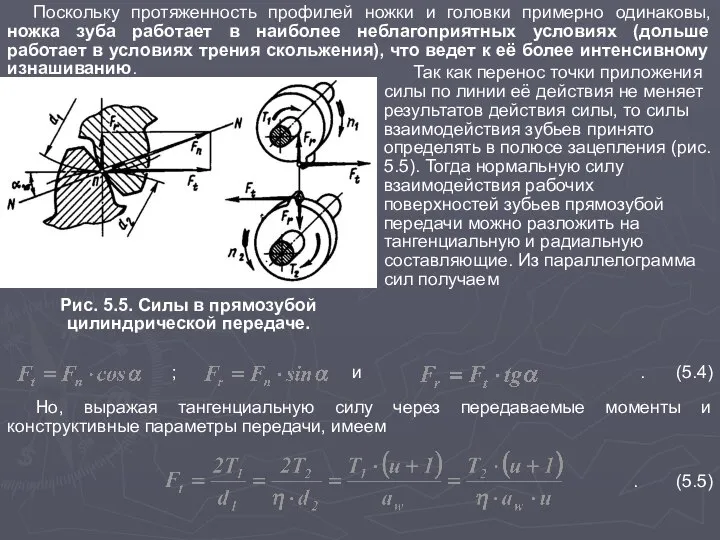
Рис. 5.5. Силы в прямозубой
цилиндрической передаче.
Так как перенос точки приложения силы по линии её действия не меняет результатов действия силы, то силы взаимодействия зубьев принято определять в полюсе зацепления (рис. 5.5). Тогда нормальную силу взаимодействия рабочих поверхностей зубьев прямозубой передачи можно разложить на тангенциальную и радиальную составляющие. Из параллелограмма сил получаем
; и . (5.4)
Но, выражая тангенциальную силу через передаваемые моменты и конструктивные параметры передачи, имеем
. (5.5)

В косозубой передаче за счет наклона продольной оси зуба к образующей делительного цилиндра кроме тангенциальной и радиальной сил появляется осевая сила (рис. 5.6).Соотношения между составляющими силы взаимодействия зубьев в этом случае будут следующими:
; . И (5.6)
При этом соотношения (5.5), связывающие тангенциальную силу с геометрическими параметрами передачи, остаются теми же самыми.

Рис. 5.7. Силы в прямозубой
конической передаче.
В конической зубчатой передаче как и в цилиндрической косозубой появляются осевые составляющие силы взаимодействия зубьев, но причиной их возникновения является наклонное расположение зубьев. Силы в конической зубчатой передаче обычно приводятся к плоскости серединного сечения зубчатого венца (рис. 5.7).
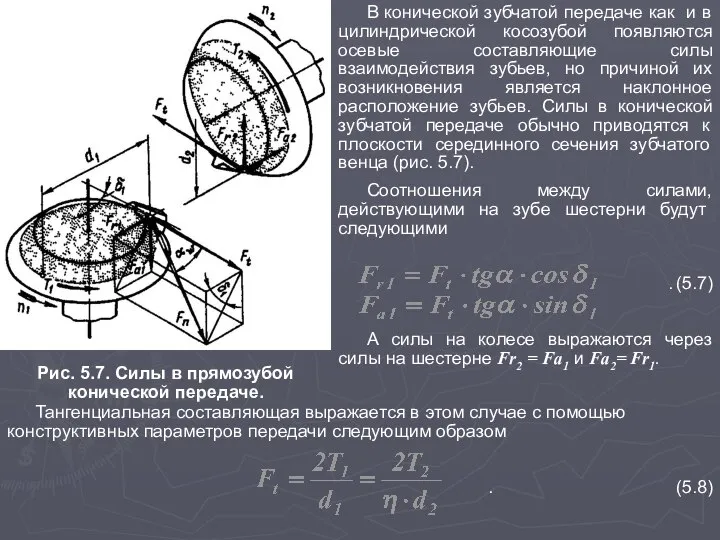
Соотношения между силами, действующими на зубе шестерни бу­дут следующими
. (5.7)
А силы на колесе выражаются через силы на шестерне Fr2 = Fa1 и Fa2= Fr1.
Тангенциальная составляющая выражается в этом случае с помощью конструктивных параметров передачи следующим образом
. (5.8)

Расчет ЦКЗП.
Основными критериями работоспособности закрытых зубчатых передач, обеспеченных достаточным количеством смазки является контактная прочность взаимодействующих поверхностей зубьев и прочность зубьев на изгиб.
При недостаточной контактной прочности рабочих поверхностей зубьев на этих поверхностях в области ножки происходит прогрессирующее усталостное выкрашивание металла, нарушающее геометрию зацепления и ослабляющее поперечное сечение зуба по отношению к изгибным напряжениям, что в конечном итоге приводит к усталостному излому зуба.
Таким образом расчет ведется из условия
и (5.9)
При проектном расчете цилиндрических передач вначале вычисляется межосевое расстояние передачи
; (5.10)
где для прямозубой передачи Ka = 450 (Н/мм2)1/3;
для косозубой передачи Ka = 410 (Н/мм2)1/3;

KH – коэффициент нагрузки, учитывающий условия работы зубьев и качество их рабочих поверхностей и состоящий из произведения нескольких других коэффициентов; T1 – вращающий момент на шестерне, Нм; u - передаточное число передачи; [σ]H – допускаемые напряжения для материалов, из которых изготовлены зубчатые колеса передачи, МПа ψba – коэффициент ширины зубчатого венца колеса (венец шестерни обычно выполняется на 2…4 мм шире зубчатого венца колеса), изменяющийся обычно в пределах 0,2…0,5 в зависимости от способа закрепления валов, несущих зубчатые колеса. Полученное значение aw округляется до ближайшего большего стандартного значения.
Ширина зубчатого венца колеса в этом случае составит
. (5.11)
Далее определяется минимально допустимое значение модуля передачи
; (5.12)
где Km = 3,4⋅103 для прямозубых передач и
Km = 2,8⋅103 для косозубых передач;
KF – коэффициент нагрузки, зависящий от точности изготовления передачи, режима её работы и качества материалов зубчатых колес.

Максимально возможное значение модуля зацепления определяют из условия неподрезания зубьев шестерни у основания
. (5.13)
В полученном диапазоне mmin…mmax выбирают стандартное значение модуля, учитывая, что при малом значении модуля увеличивается коэффициент перекрытия зубьев, повышается КПД, снижается уровень шума, уменьшаются отходы металла в стружку, сокращается трудоемкость изготовления колеса, но при больших значениях модуля передача менее чувствительна к неточности межосевого расстояния, выше изгибная прочность зубьев её колес.
Для косозубой передачи определяем минимальный угол наклона зуба
(5.14)
Далее определяют числа зубьев шестерни и колеса
и (5.14)
Полученные расчетом числа зубьев округляют до ближайшего целого значения и уточняют фактическое передаточное число и фактический угол наклона зубьев

и (5.16)
При наличии перечисленных параметров остальные параметры передачи вычисляются по приведенным ранее формулам.
При проектном расчете конических зубчатых передач в первую очередь вычисляют внешний делительный диаметр зубчатого колеса, поскольку именно он определяет в конечном итоге максимальный габаритный размер передачи.
; (5.17)
где Kd = 165 – вспомогательный коэффициент; T2 – вращающий момент на зубчатом колесе (на выходном валу), Нм; KHβ - коэффициент неравномерности распределения нагрузки по длине зуба, зависящий от твердости поверхностей зубьев и характера закрепления валов, несущих зубчатые колеса передачи; [σ]H – допускаемые контактные напряжения для материалов из которых изготовлены зубчатые колеса; vH – коэффициент, учитывающий ослабление зубьев конической передачи по сравнению с цилиндрической, для прямозубой конической передачи vH = 0,85; u − необходимое передаточное число конической зубчатой передачи
Полученное значение внешнего делительного диаметра колеса следует округлить до ближайшего стандартного значения.
Ширину зубчатого венца можно определить по соотношению
; (5.18).

где - коэффициент ширины зубчатого венца.
Число зубьев колеса вычисляют по эмпирической формуле
; (5.19)
где коэффициент С изменяется в пределах от 11,2 до 18 в зависимости от вида термической обработки рабочих поверхностей зубьев.
Далее вычисляют число зубьев шестерни
; (5.20)
Полученные числа зубьев округляют до ближайших целых величин и определяют фактическое передаточное число uф = z2/z1 с точностью не ниже 4-х знаков после запятой.
После этого вычисляют минимально допустимый внешний окружной модуль из условия прочности зуба при изгибе

После этого вычисляют минимально допустимый внешний окружной модуль из условия прочности зуба при изгибе
; (5.21)
Далее определяют углы делительных конусов и ; внешнее конусное расстояние и среднее конусное расстояние .
Внешние диаметры вершин зубьев шестерни и колеса находят по идентичным выражениям
. (5.22)
Таким образом в настоящей лекции представлены основные соотношения, необходимые для выполнения проектного расчета цилиндрических и конических зубчатых колес с эвольвентным профилем зуба. Методику проверочного расчета, а также проектного расчета передач с неэвольвентными зубчатыми колесами можно найти в учебной и справочной литературе.