Параллельное программирование для ресурсоёмких задач численного моделирования в физике. Лекция 8

Лекция № 8
Физический факультет МГУ им М.В.Ломоносова

Содержание лекции
Использование MPI
Перемножение матриц
Решение СЛАУ итерационным методом
Решение СЛАУ методом Гаусса
Минимизация функции
Физический факультет МГУ им М.В.Ломоносова

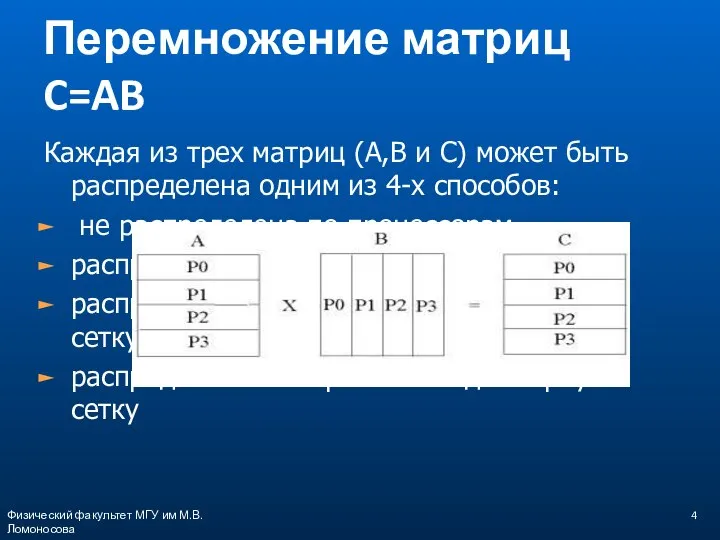
Перемножение матриц C=AB
Каждая из трех матриц (A,B и C) может быть распределена одним из 4-х способов:
не распределена по процессорам
распределена на двумерную сетку
распределена по столбцам на одномерную сетку
распределена по строкам на одномерную сетку
Физический факультет МГУ им М.В.Ломоносова

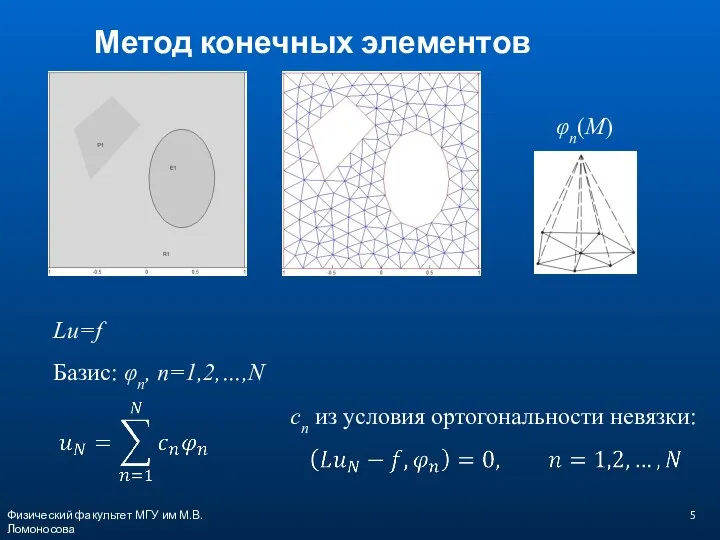
Физический факультет МГУ им М.В.Ломоносова
Метод конечных элементов
φn(M)
Lu=f
Базис: φn, n=1,2,…,N
cn из условия ортогональности невязки:

Физический факультет МГУ им М.В.Ломоносова
Решение СЛАУ итерационным методом
Одношаговые (двухслойные) итерационные методы решения СЛАУ Ay=f :
Вn+1 — итерационная матрица (det Вn+1 ≠0), τn+1>0 — итерационный параметр.
Если Вn+1=В, τn+1=τ, то метод стационарный.
Если В ≠ E, то метод неявный.

Метод релаксации (Ay=f , В=E):
Достаточное условие сходимости:
Физический факультет МГУ им М.В.Ломоносова
Метод Якоби (Ay=f , В=D, τ=1):

Решение СЛАУ методом Гаусса
Рассмотрим задачу
где A – матрица размерности NxN,
y, f - векторы размерности N
a + b + c = 6
2a – b + c = 3
-a + b – c = -2
-3b – c = -9
2b = 4
-2/3 c = -2
a = 1
b = 2
c = 3
Физический факультет МГУ им М.В.Ломоносова

Решение СЛАУ методом Гаусса
Рассмотрим задачу
где A – матрица размерности NxN,
y, f - векторы размерности N
L – нижнетреугольная матрица
U – верхнетреугольная матрица
с 1 на главной диагонали
Физический факультет МГУ им М.В.Ломоносова

Может возникнуть ситуация, когда некоторое lii << 1, тогда необходимо производить выбор главного элемента по столбцу, по строке, либо по подматрице.
В данном случае удобно осуществлять выбор по столбцу, тогда обычная перенумерация строк позволит получить достаточно большой элемент на главной диагонали. Если такого элемента нет, матрица плохо обусловлена, и решать систему данным методом нельзя.
Элементы матриц L и U:
Физический факультет МГУ им М.В.Ломоносова

double A[1:n,1:n], LU[1:n,1:n]; #предполагается, что А #инициализирована
int ps[1:n]; #индексы ведущих строк
double pivot; int pivotRow; #ведущее значение и строка
double mult; int t; #временные переменные
#инициализация ps и LU
for [i = 1 to n] {
ps[i] = i;
for [j = 1 to n]
LU[i,j] = A[i,j];
}
# исключение Гаусса с помощью ведущих элементов
for [k = 1 to n-1] { #итерации вниз по главной диагонали
pivot = abs(LU[ps[k],k]);
pivotRow = k;
Последовательная программа:
Физический факультет МГУ им М.В.Ломоносова

for [i = k+1 to n] { #выбор главного элемента в столбце k
if (abs(LU[ps[i],k]) > pivot) {
pivot = abs(LU[ps[i],k]); pivotRow = i;
}
}
if (pivotRow != k) { #перестановка строк с помощью
#перестановки указателей
t = ps[k]; ps[k] = ps[pivotRow]; ps[pivotRow] = t;
}
pivot = LU[ps[k],k];
for [i = k+1 to n] { #для всех строк в подматрице
mult = LU[ps[i],k]/pivot; #вычислить множитель
LU[ps[i],k] = mult; #и сохранить его
for [j = k+1 to n] #исключение по столбцам
LU[ps[i],j] = LU[ps[i],j] - mult*LU[ps[k],j];
}
}
Физический факультет МГУ им М.В.Ломоносова

double sum, y[1:n], f[1:n];
#прямой ход для решения Lg = f с записью g в y
for [i = 1 to n] {
sum = 0.0;
for [j = 1 to i - 1]
sum = sum + LU[ps[i],j] * y[j];
y[i] = f[ps[i]] - sum;
}
#обратный ход для решения Uy = g относительно y
for [i = n to 1 by -1] {
sum = 0.0;
for [j = i+1 to n]
sum = sum + LU[ps[i],j] * y[j];
y[i] = (y[i] - sum) / LU[ps[i],i];
}
Физический факультет МГУ им М.В.Ломоносова

Поскольку LU-разложение работает с
уменьшающимися подматрицами, объем работы
также уменьшается по мере выполнения исключений.
Схема параллельной программы
Физический факультет МГУ им М.В.Ломоносова

process Worker(w = 1 to PR) {
double LU[1:n/PR,1:n]; #свои строки LU int ps[1:n/PR]; #индексы ведущих строк
double pivot, mult, pivotRow[n];
int myRow;
декларация других локальных переменных;
инициализация ps и своих строк в LU;
#исключение Гаусса с главными элементами
for [k = 1 to n-1] { #итерации вниз по главной диагонали
поиск наибольшего главного элемента в столбце k своих строк;
обмен pivot с другими процессами;
выбор глобального максимального элемента и обновление ps;
Параллельная программа
Физический факультет МГУ им М.В.Ломоносова

if (владелец ведущей строки)
рассылка копий pivotRow другим процессам;
else
получение pivotRow;
#исключение своих строк в LU с помощью pivot и
#pivotRow
for [i = k+1 to n st (i%PR == )] { #для своей полосы
myRow = i/PR; #преобразовать индекс строки
mult = LU[ps[myRow],k]/pivot; #вычислить
#множитель
LU[ps[myRow],k] = mult; #и сохранить его
for [j = k+1 to n] #исключение по столбцам
LU[ps[myRow],j] = LU[ps[myRow],j] - mult *
pivotRow[j];
}
}
}
Физический факультет МГУ им М.В.Ломоносова

Физический факультет МГУ им М.В.Ломоносова
Минимизация функции
Метод золотого сечения:
a
b
c
d
if (f(c) < f(d)) отбросить b
else
отбросить a

Физический факультет МГУ им М.В.Ломоносова
Имеем N процессоров
a
b
x1
x2
x3
xN-2
…

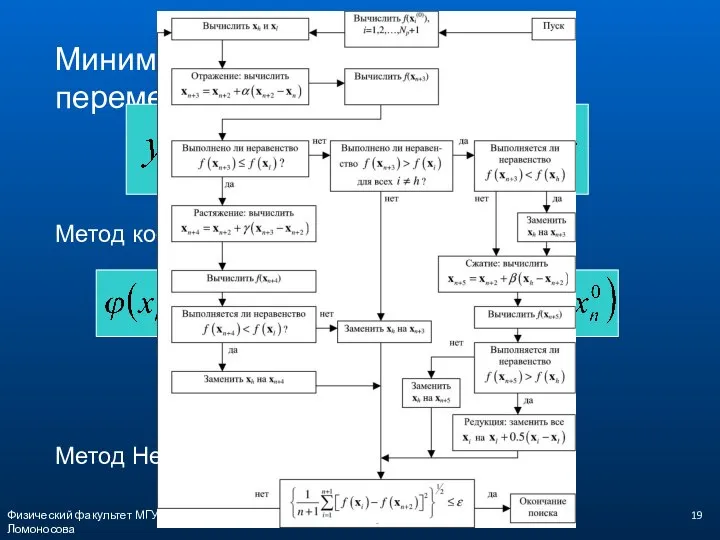
Физический факультет МГУ им М.В.Ломоносова
Минимум функции нескольких переменных
Метод координатного спуска
Метод Нелдера-Мида

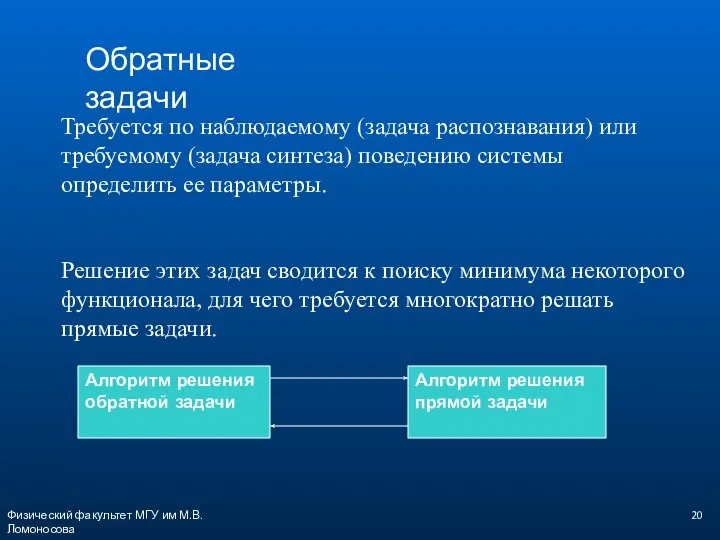
Физический факультет МГУ им М.В.Ломоносова
Обратные задачи
Требуется по наблюдаемому (задача распознавания) или
требуемому (задача синтеза) поведению системы
определить ее параметры.
Решение этих задач сводится к поиску минимума некоторого
функционала, для чего требуется многократно решать
прямые задачи.
Алгоритм решения прямой задачи
Алгоритм решения обратной задачи

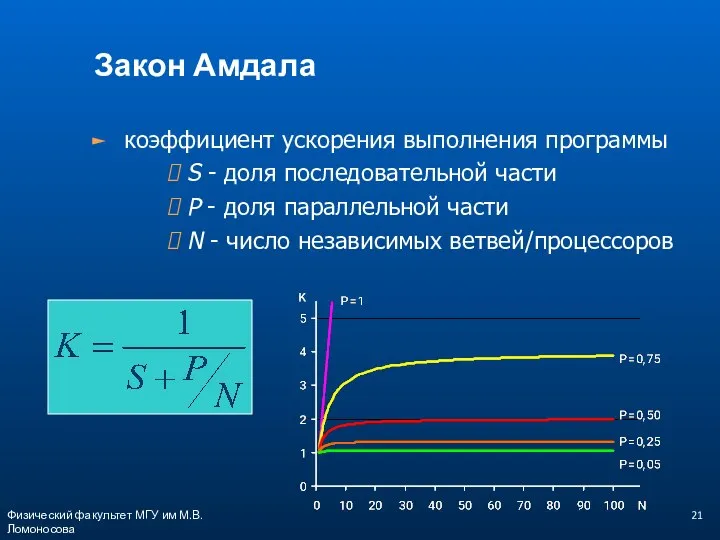
Физический факультет МГУ им М.В.Ломоносова
Закон Амдала
коэффициент ускорения выполнения программы
S - доля последовательной части
P - доля параллельной части
N - число независимых ветвей/процессоров

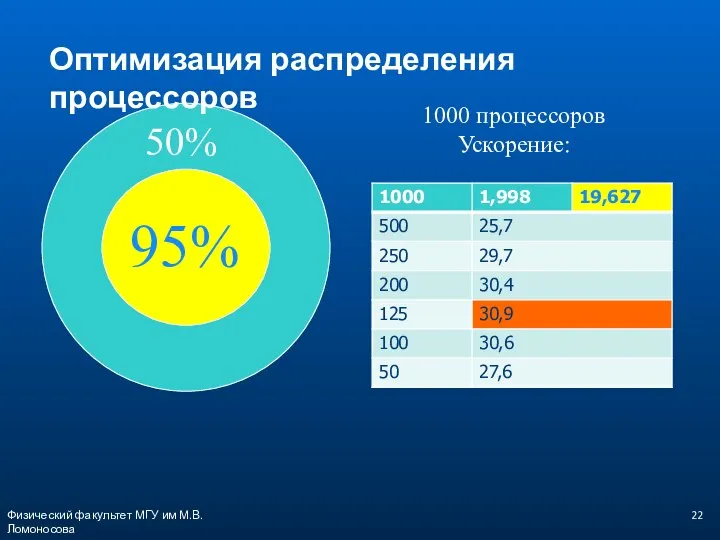
Физический факультет МГУ им М.В.Ломоносова
50%
95%
1000 процессоров
Ускорение:
Оптимизация распределения процессоров

Практическое задание
Решение системы уравнений методом Гаусса
Физический факультет МГУ им М.В.Ломоносова
Основные параметры, по которым оценивается задание:
возможность того, что число уравнений не кратно числу процессоров
блочное либо циклическое распределение по процессорам
выбор главного элемента (есть/нет)
хранение матрицы системы (по частям/целиком)
LU-разложение / Гаусс / приведение системы к диагональному виду
распределение матрицы по строкам / столбцам