Содержание
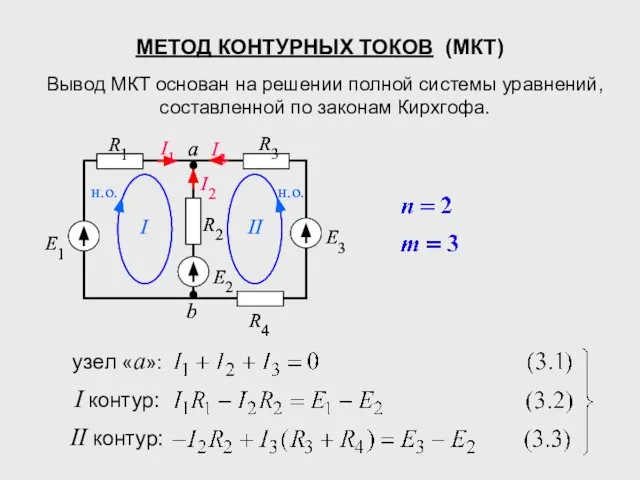
- 2. МЕТОД КОНТУРНЫХ ТОКОВ (МКТ) Вывод МКТ основан на решении полной системы уравнений, составленной по законам Кирхгофа.
- 3. Из (3.1) выразим ток внутренней ветви I2 : Подставим (3.4) в (3.2), (3.3) и приведем подобные
- 4. Из (3.1) выразим ток внутренней ветви I2 : Подставим (3.4) в (3.2), (3.3) и приведем подобные
- 5. Обозначим: (3.6)
- 6. Обозначим: контурные ЭДС (алгебраическая сумма ЭДС, входящих в контур) (3.6)
- 7. Обозначим: контурные ЭДС (алгебраическая сумма ЭДС, входящих в контур) С учетом принятых обозначений систему (3.5) можно
- 8. Структура уравнений, составленных по МКТ: В результате решения полученной системы уравнений находим контурные токи I11, I2
- 9. Порядок решения задач методом контурных токов Определить число узлов n и ветвей m схемы. 2. Выбрать
- 10. Порядок решения задач методом контурных токов Определить число узлов n и ветвей m схемы. 2. Выбрать
- 11. Порядок решения задач методом контурных токов Определить число узлов n и ветвей m схемы. 2. Выбрать
- 12. Порядок решения задач методом контурных токов Определить число узлов n и ветвей m схемы. 2. Выбрать
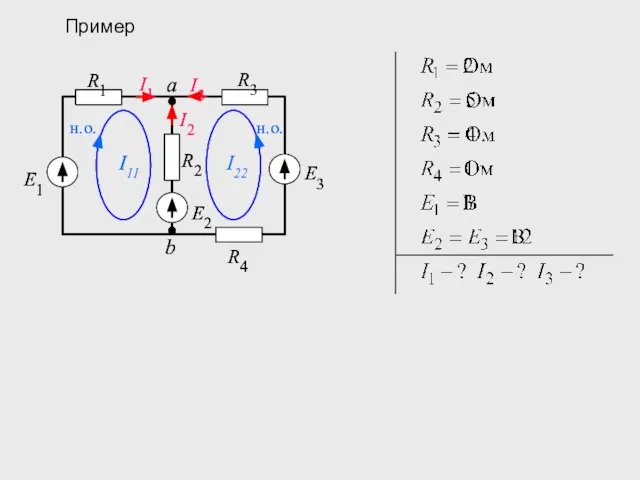
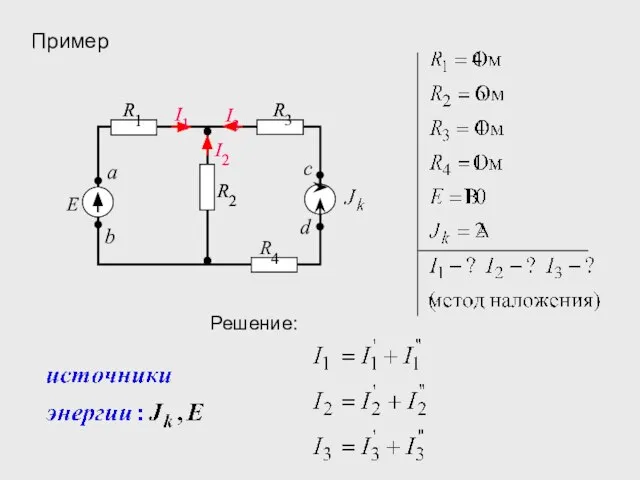
- 13. Пример
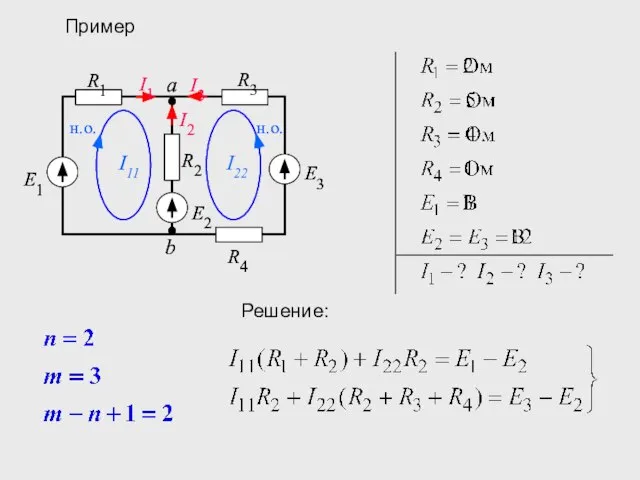
- 14. Пример Решение:
- 15. Решение полученной системы методом подстановки :
- 16. Решение полученной системы методом подстановки : Определение реальных токов в ветвях : E1 E2 E3 R1
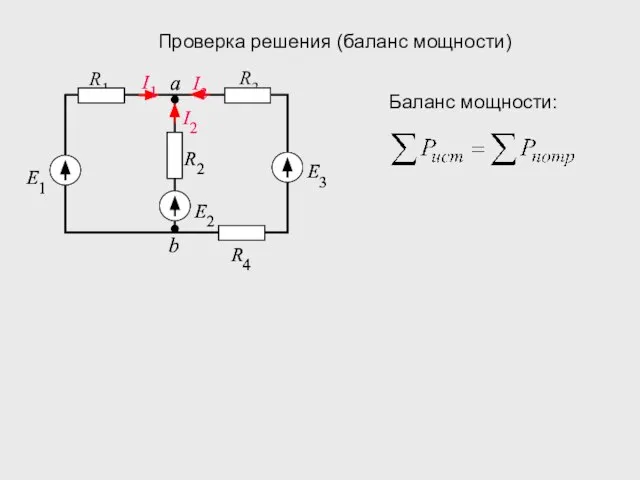
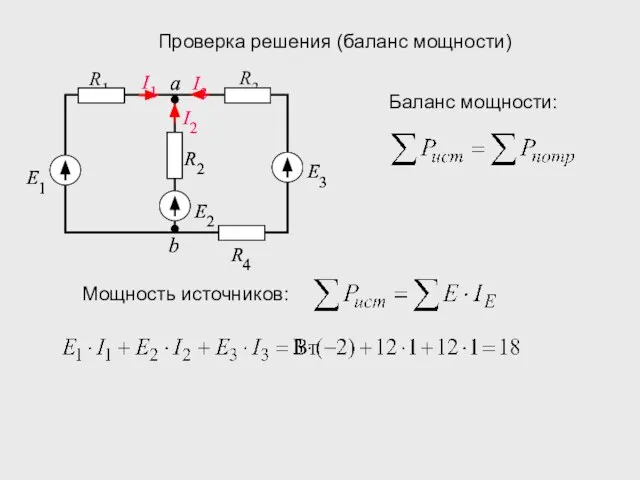
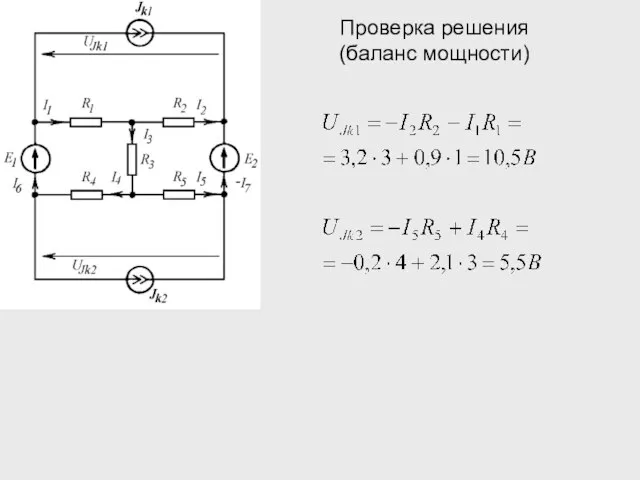
- 17. Проверка решения (баланс мощности)
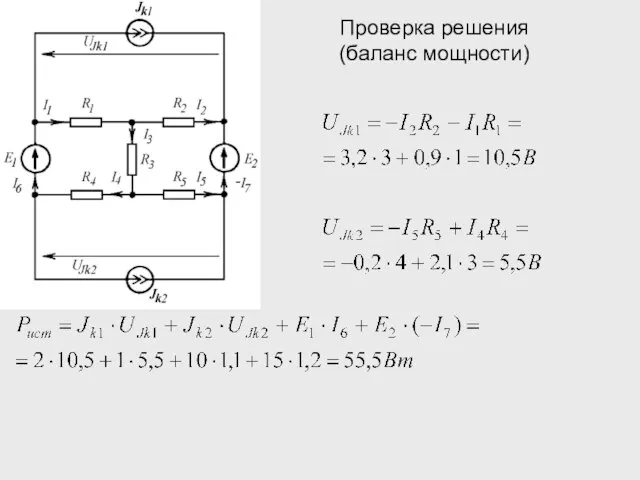
- 18. Проверка решения (баланс мощности) Мощность источников:
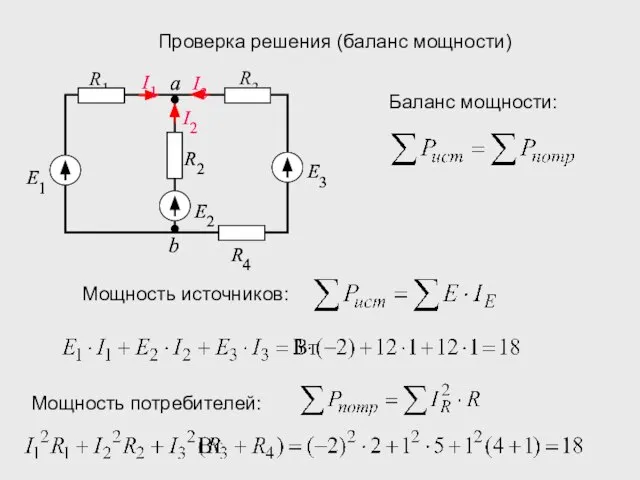
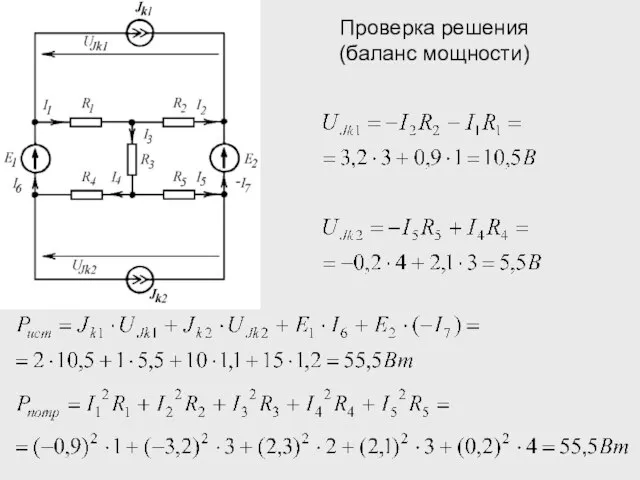
- 19. Проверка решения (баланс мощности) Мощность источников: Мощность потребителей:
- 20. Особенности применения метода контурных токов при наличии в цепи источников тока При наличии в схеме источника
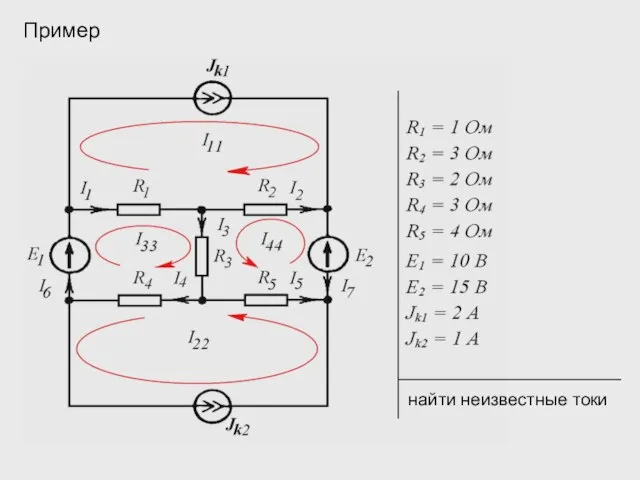
- 21. Пример найти неизвестные токи
- 22. Решение:
- 23. Решение:
- 24. Решение:
- 25. Решение полученной системы методом Крамера :
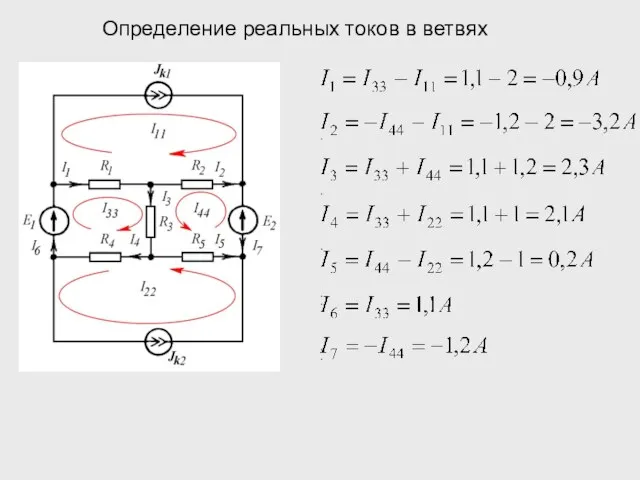
- 26. . . . . . . . Определение реальных токов в ветвях
- 27. Проверка решения (баланс мощности)
- 28. Проверка решения (баланс мощности)
- 29. Проверка решения (баланс мощности)
- 30. При расчете токов МКТ всегда можно добиться того, чтобы ветвь с искомым током входила только в
- 31. Каждую из контурных ЭДС можно выразить через ЭДС ветвей E1, E2, E3… Тогда: Ток в произвольной
- 32. Порядок решения задач методом наложения Определить число источников энергии в схеме. Количество источников энергии равно количеству
- 33. Порядок решения задач методом наложения Определить число источников энергии в схеме. Количество источников энергии равно количеству
- 34. Порядок решения задач методом наложения Определить число источников энергии в схеме. Количество источников энергии равно количеству
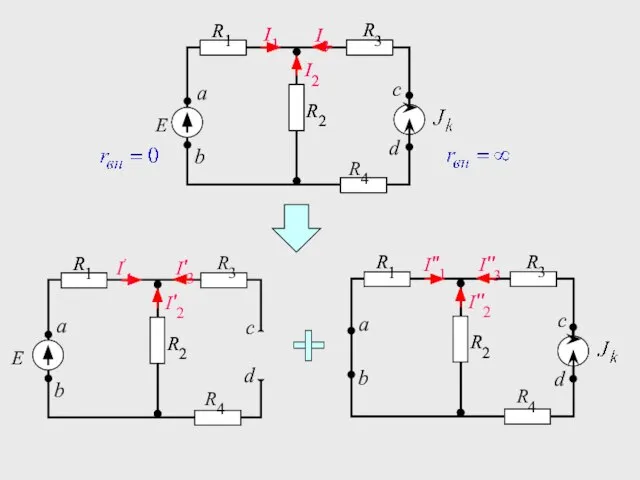
- 35. Решение: Пример
- 36. E R1 R2 R3 I1 I3 I2 R1 R2 R3 R4 I1 I3 I2 а b
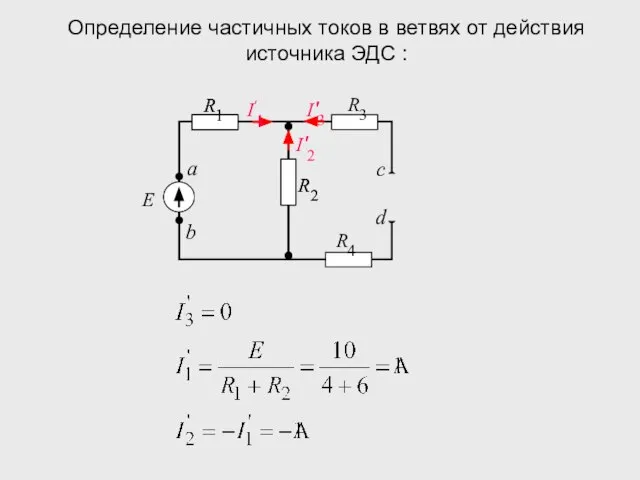
- 37. Определение частичных токов в ветвях от действия источника ЭДС :
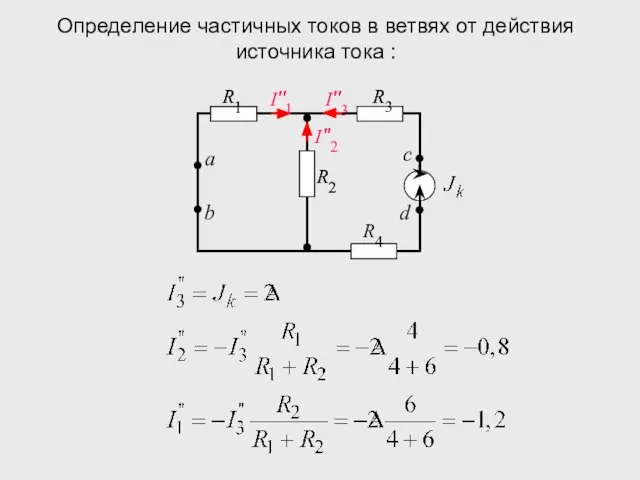
- 38. Определение частичных токов в ветвях от действия источника тока :
- 40. Скачать презентацию






















 Ускорение свободного падения на Земле и других планетах. 9 класс
Ускорение свободного падения на Земле и других планетах. 9 класс Оптимальна обробка радіотеплових сигналів
Оптимальна обробка радіотеплових сигналів Теория кварков
Теория кварков Алгоритм расчёта закрытой цилиндрической зубчатой передачи на выносливость по контактным напряжениям
Алгоритм расчёта закрытой цилиндрической зубчатой передачи на выносливость по контактным напряжениям Математическая модель канала связи
Математическая модель канала связи Длина пути машинки с крутой и пологой горки
Длина пути машинки с крутой и пологой горки Уравнение теплового баланса
Уравнение теплового баланса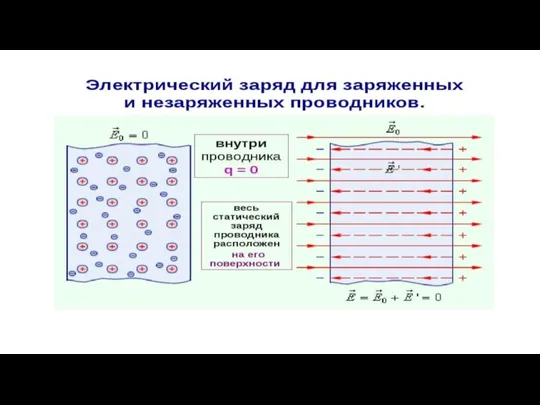 Распределение зарядов по поверхности проводника
Распределение зарядов по поверхности проводника Презентация на тему Взаимодействие электрических токов
Презентация на тему Взаимодействие электрических токов  LG_proverka_lineynogo1 (2)
LG_proverka_lineynogo1 (2) Закон сохранения импульса
Закон сохранения импульса Свободное падение тел
Свободное падение тел Магнитное поле
Магнитное поле 1664775489323__ml7bfa (1)
1664775489323__ml7bfa (1) Виды теплопередачи
Виды теплопередачи Фотоэффект
Фотоэффект Круговые процессы и их КПД. Цикл Карно
Круговые процессы и их КПД. Цикл Карно Презентация на тему Эмилий Ленц
Презентация на тему Эмилий Ленц  Полупроводники. Проводимость полупроводников
Полупроводники. Проводимость полупроводников Электрические машины. Вращающееся магнитное поле. Трехфазные асинхронные двигатели
Электрические машины. Вращающееся магнитное поле. Трехфазные асинхронные двигатели Презентация на тему Конвекция
Презентация на тему Конвекция  Решение задач по теме Соединение проводников
Решение задач по теме Соединение проводников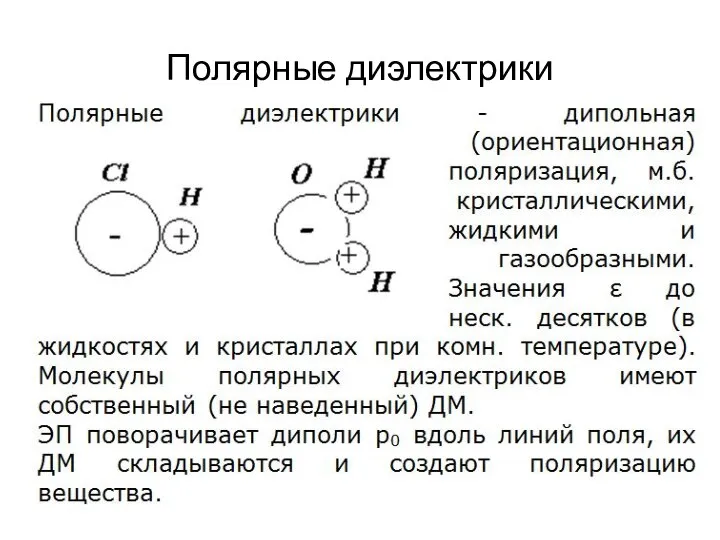 Полярные диэлектрики
Полярные диэлектрики Термодинамические циклы. Второе начало термодинамики. Энтропия. Термодинамические потенциалы
Термодинамические циклы. Второе начало термодинамики. Энтропия. Термодинамические потенциалы Интересные факты из физики. 7 класс
Интересные факты из физики. 7 класс Вимірювання проекції спіну на заданий напрямок. Експеримент Штерна-Герлаха
Вимірювання проекції спіну на заданий напрямок. Експеримент Штерна-Герлаха Отчёт о проверке автомобиля
Отчёт о проверке автомобиля Механические передачи
Механические передачи