Содержание
- 2. 09/09/2023 Тема занятия 3 Поток и ценность нейтронов. Единицы их измерения. Как зависит микроскопическое сечение поглощения
- 3. 09/09/2023 Поток нейтронов, плотность потока Поток нейтронов (плотность потока) определяется соотношением Согласно ГОСТ 19849-71 эту величину
- 4. 09/09/2023 Ценность нейтронов Ценность нейтронов ϕ+(r, E, Ω) – это решение уравнения сопряженного уравнению переноса нейтронов.
- 5. 09/09/2023 Поток нейтронов в системе удовлетворяет стационарному уравнению переноса с источником Q, в котором граничное условие
- 6. 09/09/2023 Из уравнения для функции сопряженной функции потока в реакторе следует, что функция ценности безразмерна. В
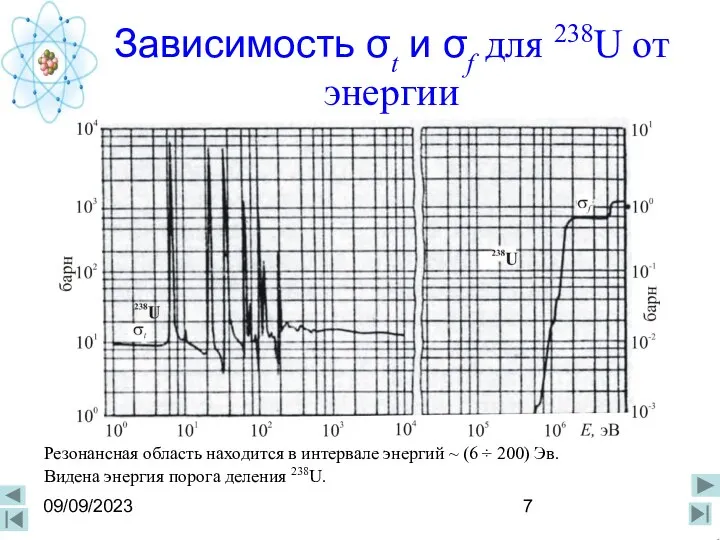
- 7. 09/09/2023 Зависимость σt и σf для 238U от энергии Резонансная область находится в интервале энергий ~
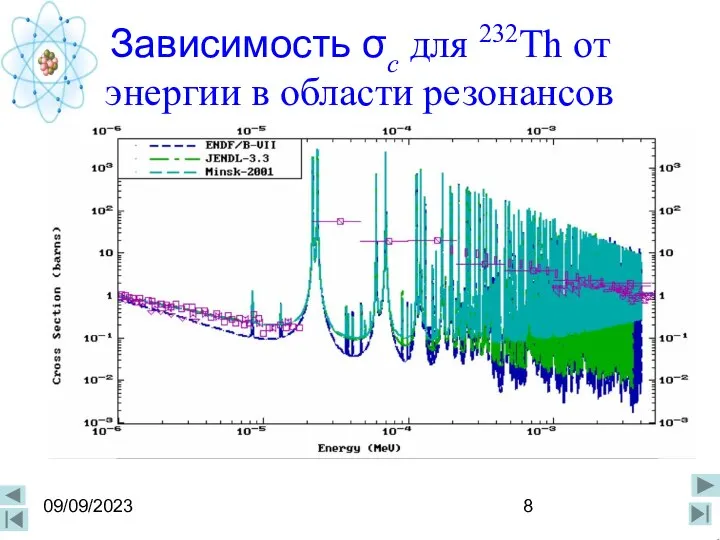
- 8. 09/09/2023 Зависимость σc для 232Th от энергии в области резонансов
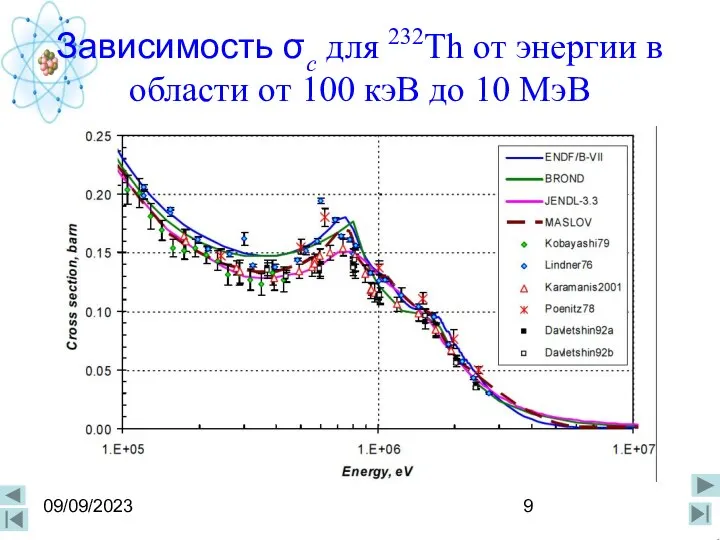
- 9. 09/09/2023 Зависимость σc для 232Th от энергии в области от 100 кэВ до 10 МэВ
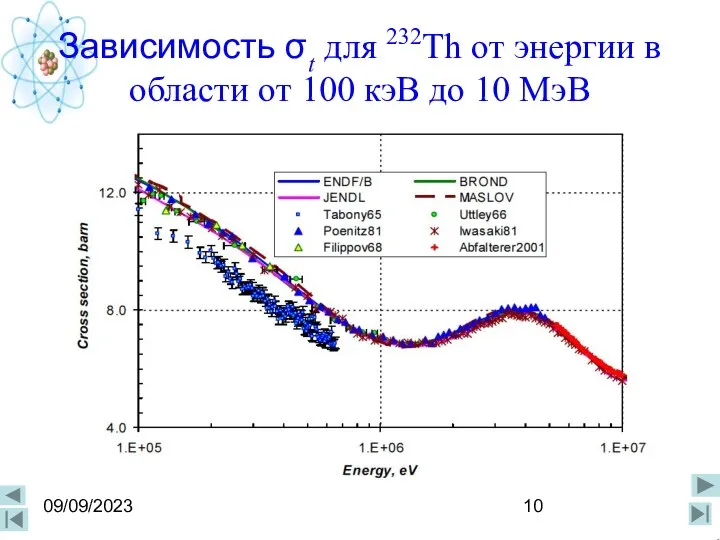
- 10. 09/09/2023 Зависимость σt для 232Th от энергии в области от 100 кэВ до 10 МэВ
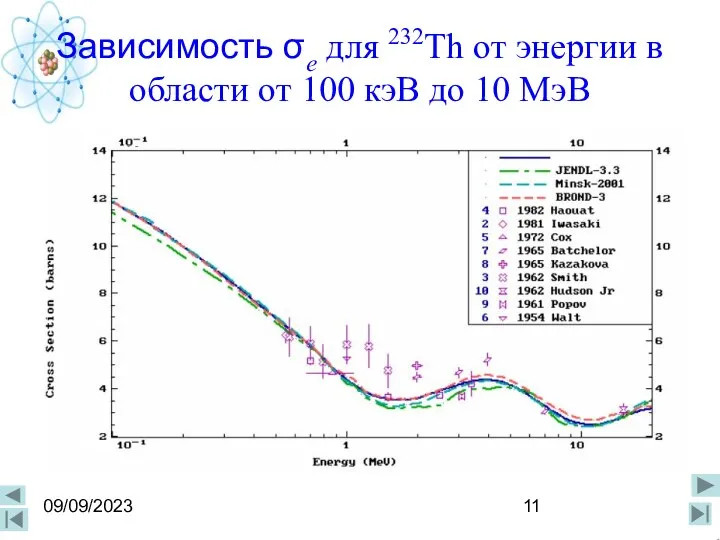
- 11. 09/09/2023 Зависимость σe для 232Th от энергии в области от 100 кэВ до 10 МэВ
- 12. 09/09/2023 Эффект Доплера при резонансном поглощении нейтронов Рассмотренные выше зависимости сечений от энергии в резонансной области
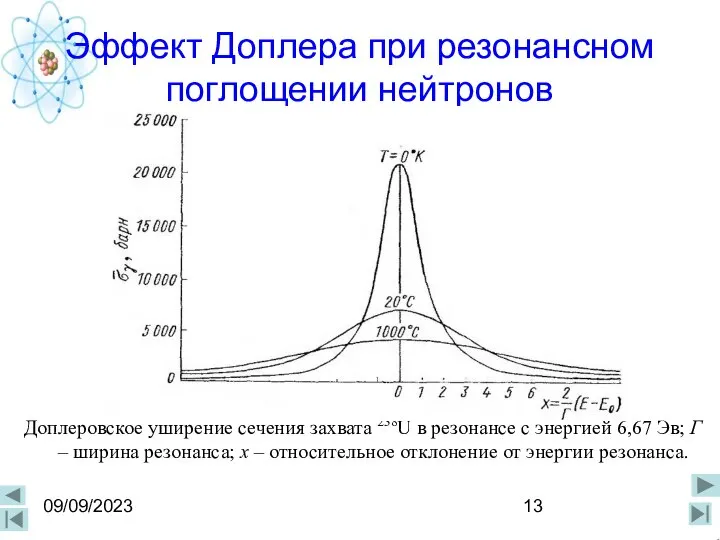
- 13. 09/09/2023 Эффект Доплера при резонансном поглощении нейтронов Доплеровское уширение сечения захвата 238U в резонансе с энергией
- 14. 09/09/2023 Уширение резонанса Как видно из рисунка, с увеличением температуры максимум резонанса снижается, а его периферийная
- 16. Скачать презентацию







 Динамика вращения. Закон динамики вращения
Динамика вращения. Закон динамики вращения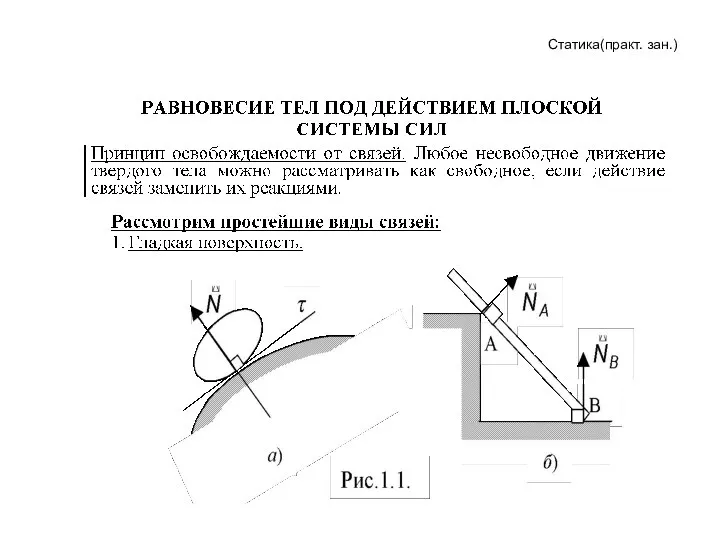 Равновесие тел под действием плоской системы сил
Равновесие тел под действием плоской системы сил Сущность фотометрических методов
Сущность фотометрических методов Ядерные реакции
Ядерные реакции Лень – двигатель прогресса или труженики с вековым стажем
Лень – двигатель прогресса или труженики с вековым стажем Логарифмы в физике
Логарифмы в физике Механический и магнитный моменты атома
Механический и магнитный моменты атома Элементарные частицы
Элементарные частицы Трактор ДТ-75
Трактор ДТ-75 Презентация на тему Законы преломления
Презентация на тему Законы преломления  Новые цели школьного физического образования – новые учебные задачи
Новые цели школьного физического образования – новые учебные задачи Электризация тел
Электризация тел Методика измерений. Виды измерений
Методика измерений. Виды измерений Унікальні фізичні властивості води
Унікальні фізичні властивості води Изменение агрегатного состояния вещества
Изменение агрегатного состояния вещества Физико-химические основы спекания ультра- и- нанодисперсных порошков TiC- Mo, полученных в процессе плазменной переконденсации
Физико-химические основы спекания ультра- и- нанодисперсных порошков TiC- Mo, полученных в процессе плазменной переконденсации Метод составления уравнений движения гибкого кольца
Метод составления уравнений движения гибкого кольца Электрические цепи переменного тока. Практическое занятие №1
Электрические цепи переменного тока. Практическое занятие №1 Презентация по физике "Решение задач на расчет работы и мощности" -
Презентация по физике "Решение задач на расчет работы и мощности" -  Физический диктант (9 класс). Взаимодействие тел. Колебания
Физический диктант (9 класс). Взаимодействие тел. Колебания Резка металла слесарной ножовкой
Резка металла слесарной ножовкой Презентация на тему Конвекция. Излучение
Презентация на тему Конвекция. Излучение  Кинематика точки
Кинематика точки Открытие нейтрона. Строение ядра. Ядерные силы
Открытие нейтрона. Строение ядра. Ядерные силы Твердотельные реле
Твердотельные реле Электричество и магнетизм. Лекция № 3
Электричество и магнетизм. Лекция № 3 Электромагниты и их применение
Электромагниты и их применение Гамма излучение
Гамма излучение