Модель Андерсона для описания магнитных примесей в металле

КРАТКАЯ ТЕОРИЯ
Примесь 0.1% и менее вызывает возникновение в металле необычных физических явлений (эффект Кондо и др.)
Причина - влияние, оказываемое на электронный спектр атомами примеси с незамкнутыми внешними d− и f−оболочками
При помещении атома примеси в кристаллическую решетку дискретные атомные уровни превращаются в электронные подзоны, ширина которых, значительно меньше, чем ширина s- и p- зон электронов проводимости

ОБОБЩЕННОЕ РЕШЕНИЕ
Из первых принципов можем построить гамильтониан (N электронов в присутстви уединенной примеси)
Для решения подобных задач подходит метод DFT при условии, что магнитный момент скомпенсирован и плотность элктронов однородна
Vimp - дополнительный потенцал, связанный с заменой одного из ядер
3-е слагаемое - спин-орбитальное взаимодействие

ПОСТРОЕНИЕ МОДЕЛИ АНДЕРСОНА
ПЕРВЫЙ ШАГ
Рассмотрим металл, зона проводимости которого образована электронами из s-атомных состояний:
1) Электроны - квазичастицы движущиеся в периодическом потенциале
2) Кулоновский потенциал экранируется
3) Пренебрегаем взаимодействием на малых расстояниях (зона широкая, состояния делокализованы)
Получаем:
Затравочный закон E(k) дисперсии определяется структурой решетки

ПОСТРОЕНИЕ МОДЕЛИ АНДЕРСОНА
ДОБАВЛЕНИЕ ПРИМЕСНОГО ИОНА
Взаимодействие электронов с примесью учтем через функции Ванье
Vk - матричный элемент гибридизации
В данном случае R - любой вектор решетки, k - квазимпульс электронов
Na - число ячеек Вигнера-Зейца в кристалле, ψ - волна Блоха
Φd - волновая функция d оболочки магнитоного иона

ПОСТРОЕНИЕ МОДЕЛИ АНДЕРСОНА
МОДЕЛЬ БЕЗ ВЗАИМОДЕЙСТВИЯ
Построенный на первых принципах гамильтониан без учета кулоновского взаимодействия, можно переписать
Модель Андерсона без взаимодействия
Для получения конечной модели нужно учесть кулоновский член на d орбитали

ПОСТРОЕНИЕ МОДЕЛИ АНДЕРСОНА
ФИНАЛЬНЫЙ ШАГ
Кулоновский интеграл:
Для атомных d орбиталей U принимает значения до 30 эВ, что существенно
При помещении иона в решетку U уменьшается до 1-7 эВ
Итоговое выражение
1,3 члены - кинетические слагаемые; 2 - потенциальное; 4 - гибридизация

ПАРАЛЛЕЛИ С МОДЕЛЬЮ ХАББАРДА
Общий вид модели Хаббарда
Общий вид модели Андерсона
Если не учитывать кинетические члены, математически модели выглядят практически идентично, хоть и несут разный смысл

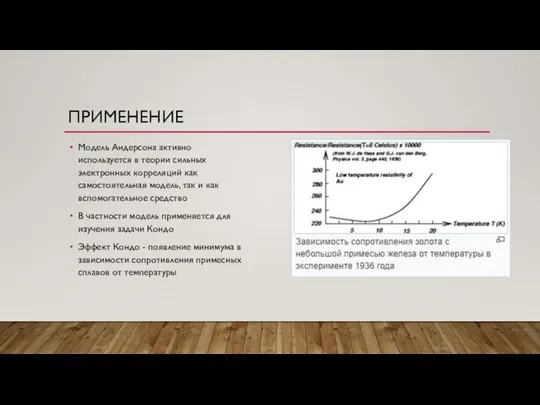
ПРИМЕНЕНИЕ
Модель Андерсона активно используется в теории сильных электронных корреляций как самостоятельная модель, так и как вспомогательное средство
В частности модель применяется для изучения задачи Кондо
Эффект Кондо - появление минимума в зависимости сопротивления примесных сплавов от температуры

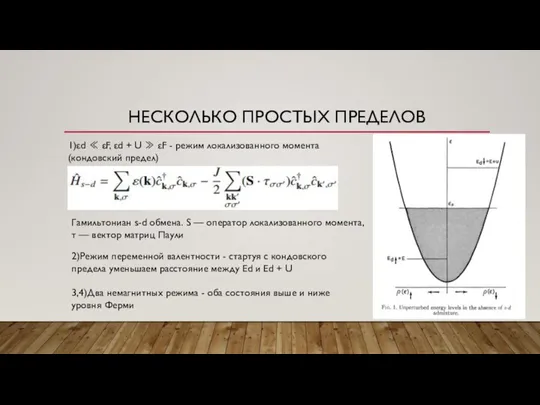
НЕСКОЛЬКО ПРОСТЫХ ПРЕДЕЛОВ
1)εd ≪ εF, εd + U ≫ εF - режим локализованного момента (кондовский предел)
2)Режим переменной валентности - стартуя с кондовского предела уменьшаем расстояние между Ed и Ed + U
3,4)Два немагнитных режима - оба состояния выше и ниже уровня Ферми
Гамильтониан s-d обмена. S — оператор локализованного момента, τ — вектор матриц Паули