что модуль
и от времени не зависит. Однако
эксперимент показывает, что при приближении системы к состоянию равновесия все
недиагональные элементы матрицы плотности стремятся к нулю. Это связано с тем, что
в
действительности рассматриваемые нами микросистемы взаимодействуют с термостатом.
Учтем действие термостата феноменологически. Опыт показывает, что
стремится к нулю по экспоненциальному закону. Это можно учесть добавкой слагаемого
в уравнение для недиагональных элементов:
,
где
- время релаксации, определяемое из эксперимента. Решение
данного уравнения
следующее:
,
причем
.
За время
элементы матрицы плотности по модулю
уменьшаются в
e
раз. Числа
образуют квадратную матрицу, ввиду
самосопряженности
матрицы
являющуюся симметричной:
.











 Криволинейное движение. Движение тела по окружности
Криволинейное движение. Движение тела по окружности Urok_Osnovy_MKT
Urok_Osnovy_MKT Постоянный электрический ток
Постоянный электрический ток Цепи синусоидального тока. Лекция 6
Цепи синусоидального тока. Лекция 6 Термодинамика фазовых превращений в однокомпонентных системах
Термодинамика фазовых превращений в однокомпонентных системах Скорость. Единицы скорости
Скорость. Единицы скорости Решение задач с помощью законов Ньютона
Решение задач с помощью законов Ньютона Вклад советских учёных-физиков в Великую Победу
Вклад советских учёных-физиков в Великую Победу Презентация на тему Химические действия света (11 класс)
Презентация на тему Химические действия света (11 класс) 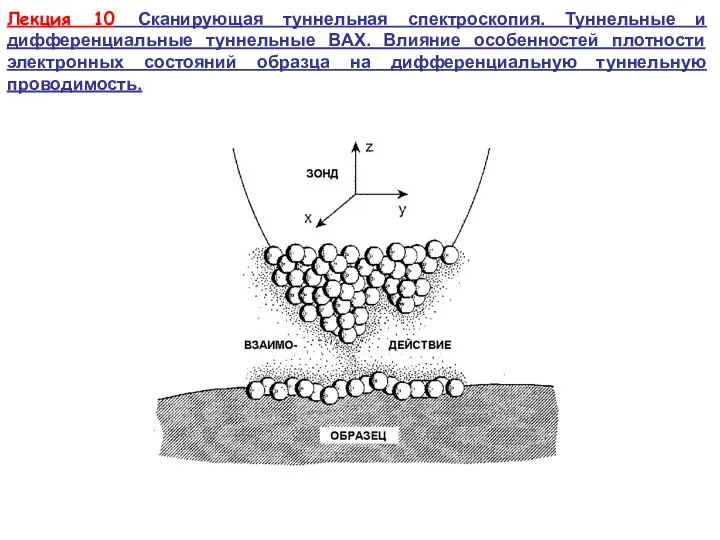 Сканирующая туннельная спектроскопия. Туннельные и дифференциальные туннельные ВАХ
Сканирующая туннельная спектроскопия. Туннельные и дифференциальные туннельные ВАХ Зубчатые передачи и их изображения на чертежах
Зубчатые передачи и их изображения на чертежах Решение задач БТ-21-1, ИСТ-21-1,2,3. Механика
Решение задач БТ-21-1, ИСТ-21-1,2,3. Механика Неисправности и ремонт системы питания дизельного двигателя
Неисправности и ремонт системы питания дизельного двигателя Действие жидкости и газа на погружённое в них тело. Урок физики в 7 классе
Действие жидкости и газа на погружённое в них тело. Урок физики в 7 классе Выпускная квалификационная работа: Проектирование шиномонтажного участка АТП
Выпускная квалификационная работа: Проектирование шиномонтажного участка АТП Механикалық тербелистер
Механикалық тербелистер Назначение основных размеров опор и определение нагрузок, действующих на опоры
Назначение основных размеров опор и определение нагрузок, действующих на опоры Физические основы микроэлектроники. Радиоматериалы и радиокомпоненты
Физические основы микроэлектроники. Радиоматериалы и радиокомпоненты Измерение мощности в трехфазной цепи
Измерение мощности в трехфазной цепи Определение толщины зуба на любом радиусе
Определение толщины зуба на любом радиусе Нейтронное излучение: опасности и перспективы
Нейтронное излучение: опасности и перспективы 11_ ОТС_ Модуляция и демодуляция 14
11_ ОТС_ Модуляция и демодуляция 14 Устройство, назначение, принцип действия подвески автомобиля
Устройство, назначение, принцип действия подвески автомобиля Презентация на тему Электрический ток (8 класс)
Презентация на тему Электрический ток (8 класс)  Модели атомов. Атом водорода по теории Бора. Тема 7
Модели атомов. Атом водорода по теории Бора. Тема 7 Презентация на тему Модели строения газа, жидкости и твердого тела
Презентация на тему Модели строения газа, жидкости и твердого тела  Миграция Кирхгофа
Миграция Кирхгофа Опрделение силы веса, координат центра тяжести и предельных значений статических углов против опрокидывания трактора
Опрделение силы веса, координат центра тяжести и предельных значений статических углов против опрокидывания трактора