Содержание
- 2. Первый закон Ньютона Существуют такие системы отсчета, относительно которых тело сохраняет состояние покоя или равномерного и
- 3. Инерциальные системы отсчета Системы отсчета, относительно которых выполняется 1 закон Ньютона, называются инерциальными. Инерциальной системой отсчета
- 4. Сила, масса, импульс Сила - это мера воздействия одного тела на другое в результате которого тела
- 5. Масса – мера инертности тела, а также мера его гравитационных свойств. При υ m = m0
- 6. Второй закон Ньютона Скорость изменения импульса материальной точки равна результирующей всех сил, действующих на эту точку:
- 7. Второй закон Ньютона (продолжение) При m=const Ускорение, приобретаемое материальной точкой, пропорционально вызывающей его силе, совпадает с
- 8. Третий закон Ньютона: Силы взаимодействия двух материальных точек равны по модулю, противоположны по направлению и направлены
- 9. Механическая система Совокупность взаимодействующих между собой тел образует механическую систему. Силы, действующие между телами, образующими систему,
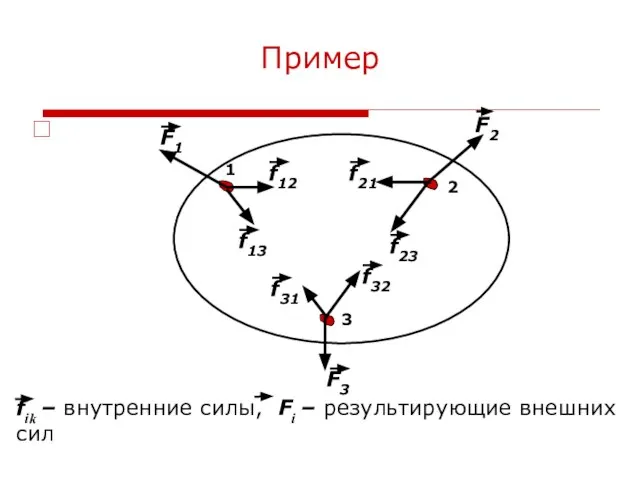
- 10. Пример 1 2 3 F1 F2 F3 fik – внутренние силы, Fi – результирующие внешних сил
- 11. Центром масс ( или центром инерции) системы материальных точек, называется точка, радиус вектор которой определяется выражением:
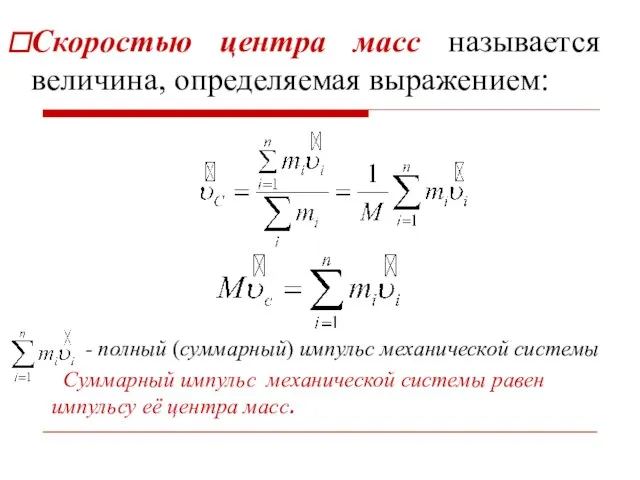
- 12. Скоростью центра масс называется величина, определяемая выражением: - полный (суммарный) импульс механической системы Суммарный импульс механической
- 13. Движение центра масс Взяв производную по времени от обеих частей равенства, получим (1) (1) – 2-ой
- 14. Закон сохранения импульса По II закону Ньютона: Система называется изолированной, если результирующая внешних сил, действующих на
- 15. Энергия и работа Энергия - универсальная количественная мера различных форм движения и взаимодействия. Она учитывает возможность
- 16. Работа переменной силы Элементарной работой силы F на перемещении dr называется скалярная величина δA= ( F,dr
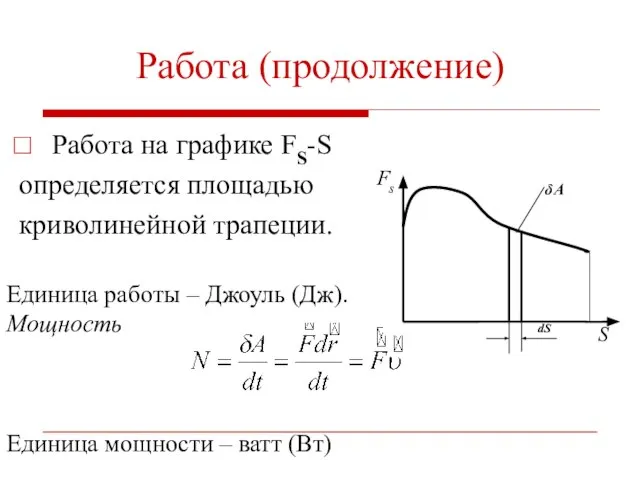
- 17. Работа (продолжение) Работа на графике FS-S определяется площадью криволинейной трапеции. Единица работы – Джоуль (Дж). Мощность
- 18. Wк = mυ2/ 2 Кинетической называется энергия движущегося тела, зависящая от его скорости. Она измеряется работой,
- 19. Консервативные и диссипативные силы Силы, работа которых зависит от того, как система переходит из одного состояния
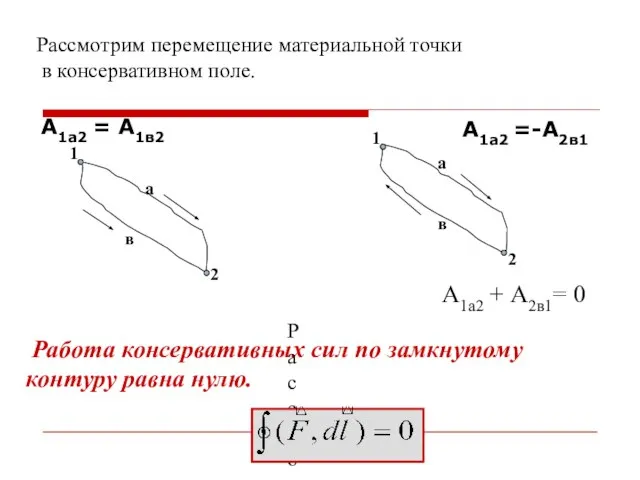
- 20. Работа консервативных сил по замкнутому контуру равна нулю. Рассмотрим перемещение материальной точки в консервативном поле. А1а2
- 21. Потенциальная энергия Если система консервативная, то её можно охарактеризовать потенциальной энергией. Потенциальная энергия - это энергия
- 22. Потенциальная энергия в частных случаях Сравнить: А12 = ∆Wк = Wк2 - Wк1 Если в потенциальном
- 24. Скачать презентацию

















 Расчёт кругового поворота автомобиля
Расчёт кругового поворота автомобиля Фильтры с бесконечной импульсной характеристикой. Построение структурных схем БИХ-фильтров
Фильтры с бесконечной импульсной характеристикой. Построение структурных схем БИХ-фильтров Решение задач
Решение задач Закон сохранения импульса. Реактивное движение
Закон сохранения импульса. Реактивное движение Тест. Физика элементарных частиц
Тест. Физика элементарных частиц Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц Радиоактивность. Человек и радиация
Радиоактивность. Человек и радиация Магнитное поле и его графическое изображение
Магнитное поле и его графическое изображение Теория относительности. (Лекция 4)
Теория относительности. (Лекция 4) Презентация на тему Сила упругости. Закон Гука. Вес тела
Презентация на тему Сила упругости. Закон Гука. Вес тела  Квантовая радиофизика
Квантовая радиофизика Обнаружение магнитного поля по его действию на электрический ток. Правило левой руки
Обнаружение магнитного поля по его действию на электрический ток. Правило левой руки Режим натуральной мощности
Режим натуральной мощности “Жарық техникасы және жарық көздері” пәні бойынша оқу-әдістемелік кешенін жасақтау
“Жарық техникасы және жарық көздері” пәні бойынша оқу-әдістемелік кешенін жасақтау Механические колебания
Механические колебания Электроосветительные установки
Электроосветительные установки Презентация на тему Деление ядер урана
Презентация на тему Деление ядер урана  Графики в задачах по кинематике
Графики в задачах по кинематике Условия плавания тел
Условия плавания тел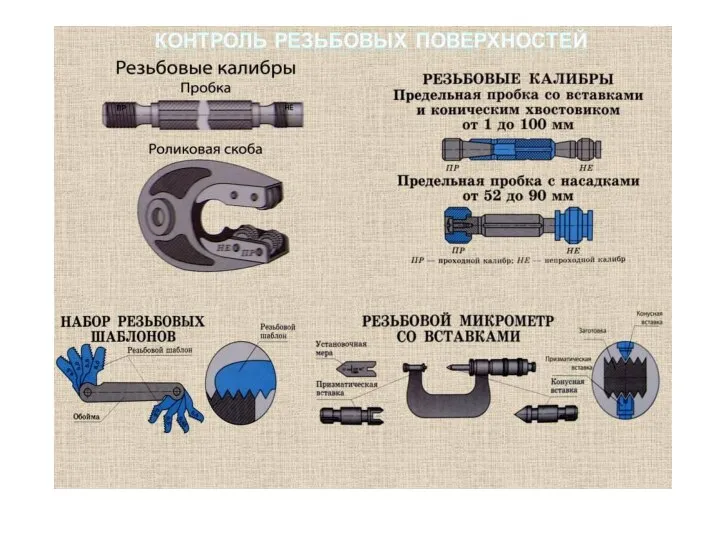 Технология обработки на металлорежущих станках. Контроль резьбовых поверхностей
Технология обработки на металлорежущих станках. Контроль резьбовых поверхностей Механические волны
Механические волны План структурной оптимизации технологического процесса изготовления кузова модели SX11
План структурной оптимизации технологического процесса изготовления кузова модели SX11 Электрический ток
Электрический ток Механические колебания и волны. Звук
Механические колебания и волны. Звук Нетрадиционные источники энергии
Нетрадиционные источники энергии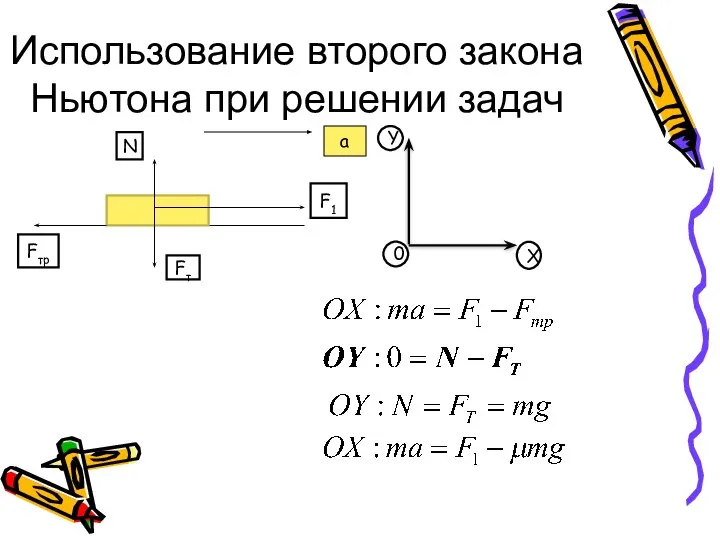 Использование второго закона Ньютона при решении задач
Использование второго закона Ньютона при решении задач Дисперсия света. Опыт И. Ньютона
Дисперсия света. Опыт И. Ньютона Предмет механики. Аксиомы статики. Связи и реакции связей. Система сходящихся сил. Равнодействующая сходящихся сил
Предмет механики. Аксиомы статики. Связи и реакции связей. Система сходящихся сил. Равнодействующая сходящихся сил