параметры, которые определяют процесс колебания механической системы:
1)P1 – М (кг), 2) Р2 – ω (с−1), 3) Р3 – F (кг⋅м/с2),
4) Р4 – S (м), 5) P5 – μ (кг/с), 6) P6 − c (кг/с2),
7) P7 − t (c).
Участвующих величин будет семь (m = 7). Функциональная зависимость, подлежащая исследованию, получит вид:
Ф(Р1, Р2, Р3, Р4, Р5, Р6, Р7) = 0 или Ф(М, ω, F, S, μ, с, t) = 0, где Р1, Р2 ,…, Р7 − параметры системы.
2. Выберем три (k = 3) независимые единицы применительно к системе измерений LMT (здесь L – линейный размер, м; М − масса, кг; Т − время, с). В качестве основных (базисных) параметров примем: P1 = М, кг; Р2 = ω, с−1, P3 = F, кг⋅м/с2.

![3. Определяем размерность каждого основного (базисного) параметра: P1 = [M] = [L]0](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/967096/slide-2.jpg)










 Основы технической механики
Основы технической механики Все о звуке
Все о звуке Короткое замыкание. Предохранители
Короткое замыкание. Предохранители Презентация на тему Работа и мощность тока
Презентация на тему Работа и мощность тока  Подводные индикаторы наклона типа Bullseye производства I-TECH
Подводные индикаторы наклона типа Bullseye производства I-TECH Сверхпроводимость материалов
Сверхпроводимость материалов Разложение вектора по трём некомпланарным векторам
Разложение вектора по трём некомпланарным векторам еометрическая оптика
еометрическая оптика Решение задач , подготовка к контрольной кинематика
Решение задач , подготовка к контрольной кинематика Зависимость сопротивления от температуры сверхпроводимость
Зависимость сопротивления от температуры сверхпроводимость Электростатика. Заря́д
Электростатика. Заря́д Реактивное движение. Ракеты
Реактивное движение. Ракеты Равновесие. Ключевые слова
Равновесие. Ключевые слова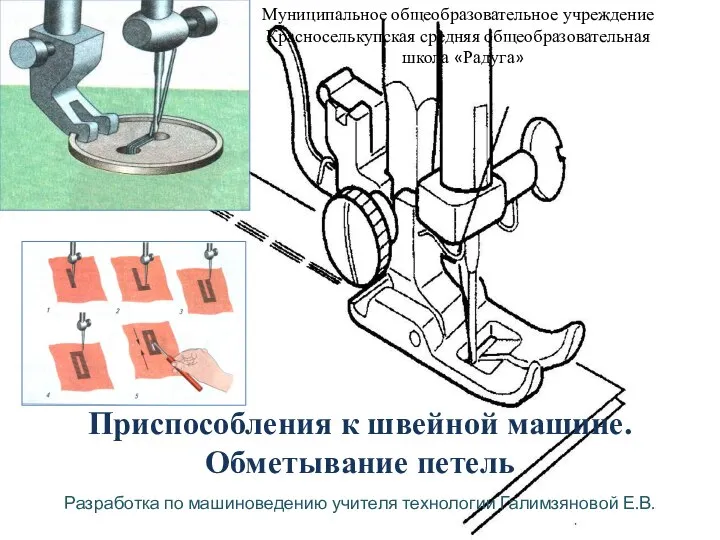 Приспособления к швейной машине. Обметывание петель
Приспособления к швейной машине. Обметывание петель Презентация на тему Тепловое равновесие
Презентация на тему Тепловое равновесие  Инфракрасное излучение в помощь школе
Инфракрасное излучение в помощь школе Кинематика. 8 класс
Кинематика. 8 класс Сила — векторная величина
Сила — векторная величина Медицинское открытие. Бионические контактные линзы
Медицинское открытие. Бионические контактные линзы Вимірювання проекції спіну на заданий напрямок. Експеримент Штерна-Герлаха
Вимірювання проекції спіну на заданий напрямок. Експеримент Штерна-Герлаха Аккумуляторная батарея
Аккумуляторная батарея Испарение и конденсация. Поглощение и выделение энергии
Испарение и конденсация. Поглощение и выделение энергии Презентация на тему Первый урок физики
Презентация на тему Первый урок физики  Оптика. Законы отражения
Оптика. Законы отражения Валерий Брюсов “Мир электрона”. (1922г)
Валерий Брюсов “Мир электрона”. (1922г) Ремонт центробежного водяного насоса
Ремонт центробежного водяного насоса Презентация на тему Закон всемирного тяготения. Движение планет
Презентация на тему Закон всемирного тяготения. Движение планет  Дифракция механических волн
Дифракция механических волн