Определение уравнения движения. Общий случай интегрального уравнения

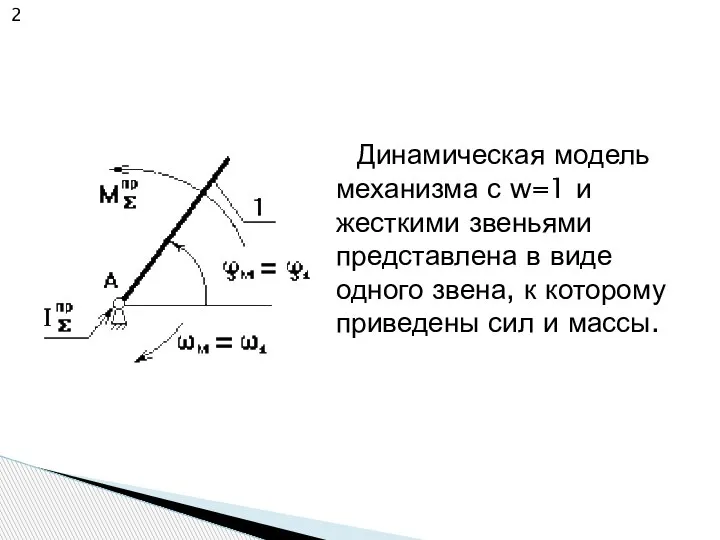
Динамическая модель механизма с w=1 и жесткими звеньями представлена в виде одного звена, к которому приведены сил и массы.

Закон движения выбранного звена может быть найден по приведенным параметрам динамической модели
Теорема об изменении кинематической энергии :
Получаем:
Где

Сумму работ можно представить в виде интеграла с переменным верхним пределом ψ от суммарного приведенного момента по углу поворота, поэтому:

Закон движения ω(ψ) звена приведения представляет решение предыдущего уравнения в виде функции обобщенной координаты ψ

Продифференцировав выражение суммы работ по координате ψ, получим дифференциальное уравнение движения:

Учитывая, что , получаем дифференцированием
угловое ускорение звена приведения

МА можно представить как одно звено с переменным моментом инерции, в общем случае зависящим от обобщенной координаты ψ.
Алгоритм расчета динамической модели строиться в виде функции ψ(независимая переменная).

Свяжем расчетные значения ψ со временем. Проинтегрируем и получим:
При:

Определение соответствующих моментов времени движения связано с интегрированием обратной функции
Вывод