Газовые законы

Газовые законы
Количественные зависимости между двумя из параметров состояния газа (р, V, T), когда третий параметр и масса газа не меняются, называются газовыми законами.
Изопроцессы
Процессы изменения состояния системы, при которых один из параметров состояния газа не меняется, называются изопроцессами:
1) изотермическим, 2) изобарическим и 3) изохорическим.
Изотермический процесс
Изотермическим называется процесс изменения состояния системы, проходящий при постоянной температуре:
Изобарический процесс
Изобарическим называется процесс изменения состояния системы, проходящий при постоянном давлении:
Изохорический процесс
Изохорическим называется процесс изменения состояния системы, проходящий при постоянном объеме:

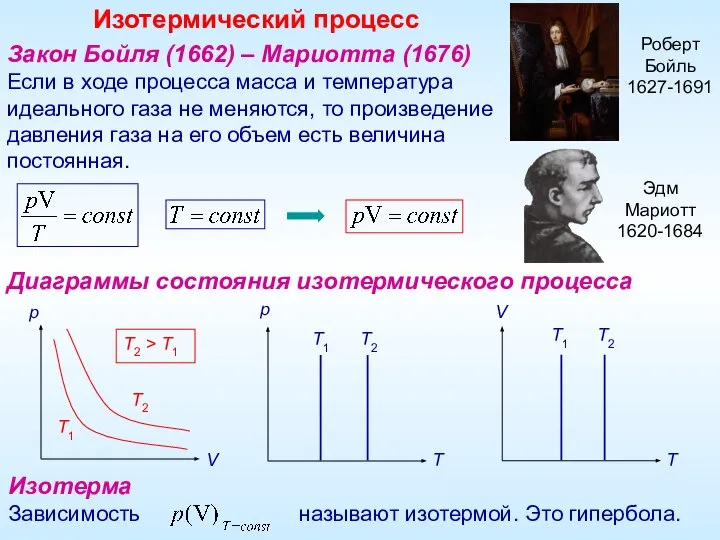
Закон Бойля (1662) – Мариотта (1676)
Если в ходе процесса масса и температура
идеального газа не меняются, то произведение
давления газа на его объем есть величина
постоянная.
Диаграммы состояния изотермического процесса
V
T
T
p
V
p
T2
T1
T1
T2
T2
T1
Изотерма
Зависимость называют изотермой. Это гипербола.
Изотермический процесс
T2 > T1
Роберт
Бойль
1627-1691
Эдм
Мариотт
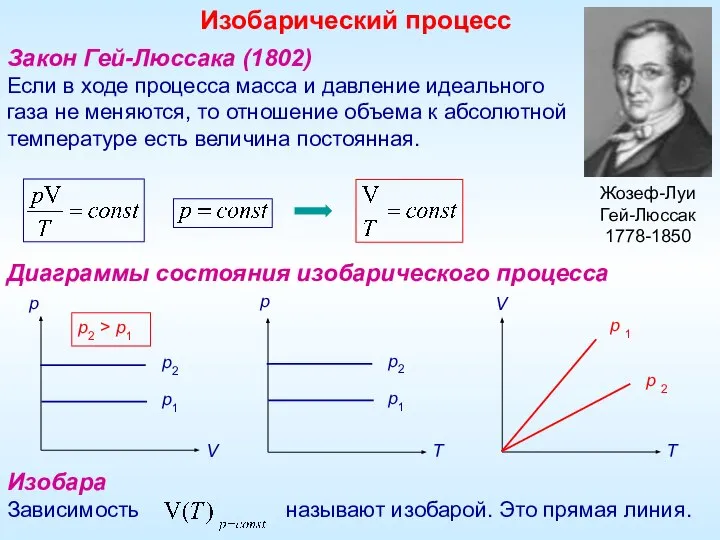
1620-1684

Закон Гей-Люссака (1802)
Если в ходе процесса масса и давление идеального
газа не меняются, то отношение объема к абсолютной
температуре есть величина постоянная.
Диаграммы состояния изобарического процесса
V
T
T
p
V
p
p 2
p 1
p2
p1
Изобара
Зависимость называют изобарой. Это прямая линия.
Изобарический процесс
p2 > p1
p2
p1
Жозеф-Луи
Гей-Люссак
1778-1850

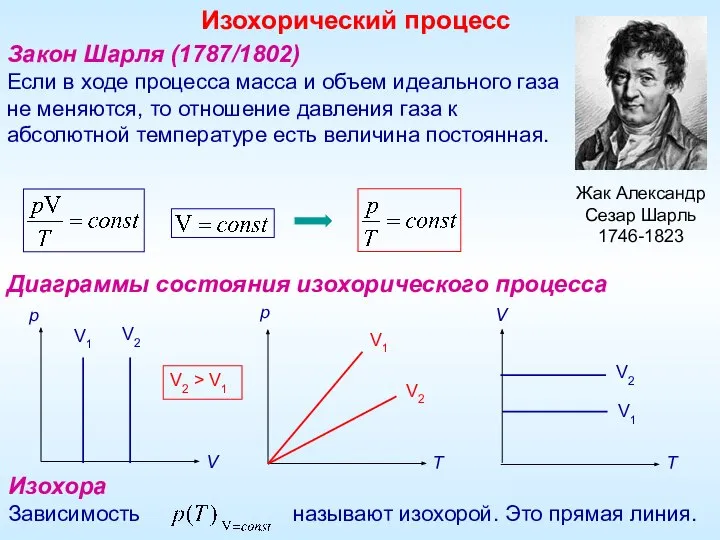
Закон Шарля (1787/1802)
Если в ходе процесса масса и объем идеального газа
не меняются, то отношение давления газа к
абсолютной температуре есть величина постоянная.
Диаграммы состояния изохорического процесса
V
T
T
p
V
p
V2
Изохора
Зависимость называют изохорой. Это прямая линия.
Изохорический процесс
V2 > V1
V1
V2
V1
V2
V1
Жак Александр
Сезар Шарль
1746-1823

Объемное тепловое расширение газов
Закон Гей-Люссака в другом виде: чему равен объем газа V при температуре t °C, если при температуре t0 = 0 °C = 273 K объем V0:
При нагревании при постоянном давлении на 1 °С объем некоторой массы газа увеличивается на 1/273 часть того объема, который эта масса газа занимала при t = 0 °C.
Коэффициент объемного расширения
Коэффициенты объемного расширения всех газов одинаковы и равны 1/T0 = 1/273 K–1.
Давление при тепловом расширение газов
Закон Шарля в другом виде:
Давление некоторой массы газа при нагревании его при постоянном объеме на 1 °С увеличивается на 1/273 часть того давления, который этот газ имел при t = 0 °C.

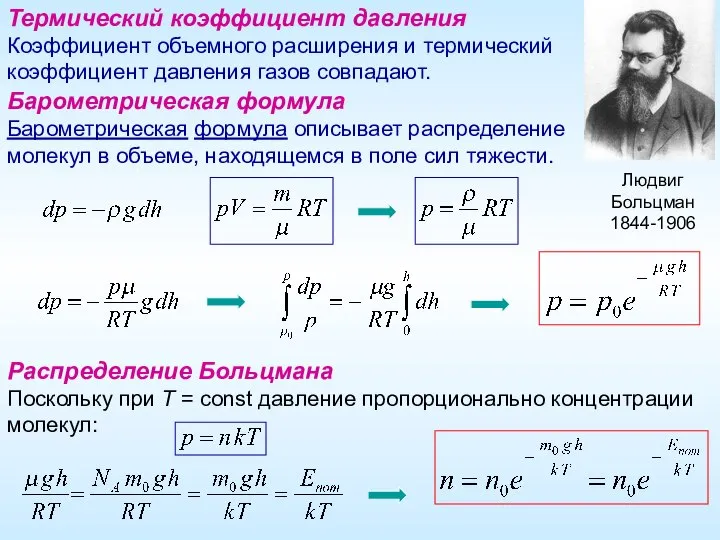
Термический коэффициент давления
Коэффициент объемного расширения и термический
коэффициент давления газов совпадают.
Барометрическая формула
Барометрическая формула описывает распределение
молекул в объеме, находящемся в поле сил тяжести.
Распределение Больцмана
Поскольку при Т = const давление пропорционально концентрации молекул:
Людвиг
Больцман
1844-1906

Явления переноса
В отсутствии равновесия в газе имеются пространственные неоднородности параметров (давления, плотности, температуры).
Если газ предоставить самому себе, то хаотическое движение молекул постепенно выравнивает эти неоднородности и газ приходит в состояние термодинамического равновесия.
Явления выравнивания сопровождаются направленным переносом ряда физических величин (массы, энергии, импульса) и поэтому называются явлениями переноса.
К явлениям переноса относятся:
1) Диффузия (перенос массы)
2) Теплопроводность (перенос энергии)
3) Внутреннее трение или вязкость (перенос импульса)
Градиент
Градиентом величины А в направлении x называется вектор, направленный в сторону возрастания этой величины, и численно равный изменению А на единицу длины этого направления.
Градиент характеризует быстроту изменения этой величины по данному направлению.

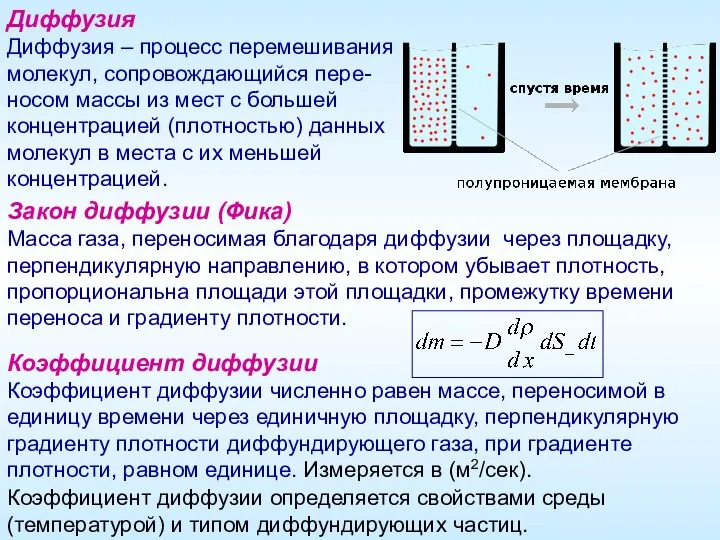
Диффузия
Диффузия – процесс перемешивания
молекул, сопровождающийся пере-
носом массы из мест с большей концентрацией (плотностью) данных
молекул в места с их меньшей
концентрацией.
Закон диффузии (Фика)
Масса газа, переносимая благодаря диффузии через площадку, перпендикулярную направлению, в котором убывает плотность, пропорциональна площади этой площадки, промежутку времени переноса и градиенту плотности.
Коэффициент диффузии
Коэффициент диффузии численно равен массе, переносимой в единицу времени через единичную площадку, перпендикулярную градиенту плотности диффундирующего газа, при градиенте плотности, равном единице. Измеряется в (м2/сек).
Коэффициент диффузии определяется свойствами среды (температурой) и типом диффундирующих частиц.

Теплопроводность
Теплопроводность – процесс выравнивания температуры тела, сопровождающийся направленным переносом тепла из более нагретых мест в менее нагретые.
Закон теплопроводности (Фурье)
Количество теплоты, переносимой благодаря теплопроводности через площадку, перпендикулярную направлению, в котором убывает температура, пропорционально площади этой площадки, промежутку времени переноса и градиенту температуры.
Коэффициент теплопроводности
Коэффициент теплопроводности численно равен количеству тепла, переносимой в единицу времени через единичную площадку, перпендикулярную градиенту температуры, при градиенте температуры, равном единице. Измеряется в (Дж/(м⋅сек⋅К).
Коэффициент теплопроводности определяется свойствами среды.

Вязкость
Вязкость – процесс выравнивания скоростей частиц тела, сопровождающийся направленным переносом импульса из более быстрых слоев в более медленные в направлении, перпендикулярном направлению движения слоев газа (жидкости).
Закон вязкого (внутреннего) трения
Импульс, переносимый благодаря вязкому трению через площадку, перпендикулярную направлению, в котором убывает скорость, пропорционален площади этой площадки, промежутку времени переноса и градиенту скорости.
Коэффициент вязкости
Коэффициент динамической вязкости численно равен силе внутреннего трения, приходящейся на единицу площади, перпендикулярную градиенту скорости, при градиенте скорости, равном единице. Измеряется в (Па⋅сек).
Коэффициент вязкости определяется свойствами среды.

Многоатомный газ
Степени свободы системы (N)
Числом степеней свободы материального объекта называется число независимых координат, которые необходимо задать, чтобы однозначно определить положение этого объекта относительно рассматриваемой системы отсчета.
Материальная точка (N=3)
Положение материальной точки в пространстве определяется тремя координатами x, y, z (три степени свободы).
Абсолютно твердое тело (N=6)
Абсолютно твердое тело имеет шесть степеней свободы – три поступательных (x, y, z) и три вращательных (θ, ϕ, ψ ).
Двухатомная молекула с жесткой связью (N=5)
Две материальные точки на неизменном расстоянии друг от друга – три поступательных и две вращательных.
Двухатомная молекула с упругой связью (N=6)
Две материальные точки на изменяющемся расстоянии друг от друга – три поступательных, две вращательных и одну колебательную (расстояние между точками).

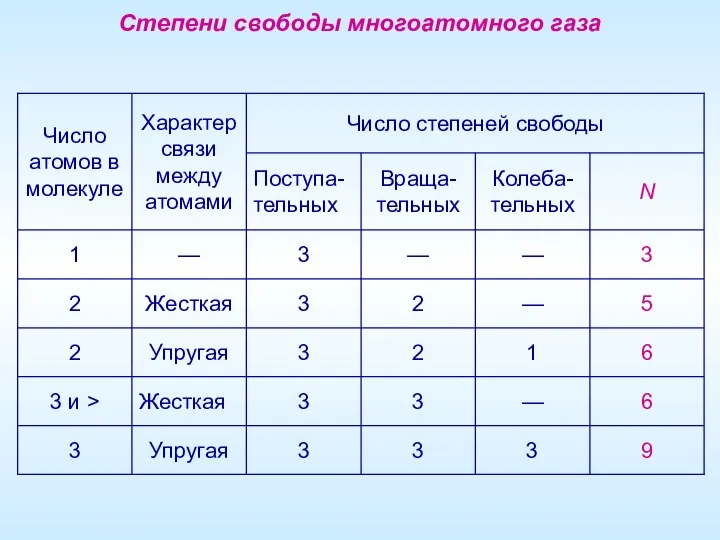
Степени свободы многоатомного газа

Средняя энергия молекул одноатомного газа
Распределение энергии по степеням свободы молекул
Поступательно двигаются только одноатомные молекулы. Двух и многоатомные молекулы могут также совершать вращательные и колебательные движения. При любом числе степеней свободы три — поступательные, причем ни одна из них не имеет преимуществ перед другими. Следовательно, на каждую поступательную степень свободы приходится в среднем одинаковая энергия
Закон о равномерном распределение
энергии по степеням свободы
На каждую степень свободы молекулы приходится равная энергия
i — сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы. При T < 1 000 K связи между атомами можно рассматривать как жесткие.

Идеальный газ
1) Молекулы действуют как точечные массы (что приблизительно соответствует действительности, если они удалены друг от друга)
2) молекулы не оказывают воздействия друг на друга (за исключением соударений).
Уравнение Ван-дер-Ваальса (1873)
Ян Дидерик
Ван-дер-Ваальс
1837-1923
Ноб. лаур.
1910
Реальные газы
1) Поправка на недоступный для движения объем.
2) Поправка на силы притяжения молекул (внутреннее давление).
Rm~10-10 м
Vm~4⋅10-30 м3
В 1 м3 при нормальных условиях N~2.7⋅1025
Vc~1.2⋅10-4 м3
~0.0001 V
При p~5000 атм
V~2⋅10-4 м3

Уравнение Ван-дер-Ваальса (1873)
Для 1 моля:
Для молей:
Значение уравнения Ван-дер-Ваальса:
1) уравнение было получено из модельных представлений о свойствах реальных газов и жидкостей, а не явилось результатом эмпирического подбора функции f (p, V, T), описывающей свойства реальных газов;
2) уравнение долго рассматривалось как некоторый общий вид уравнения состояния реальных газов, на основе которого было построено много других уравнений состояния;
3) с помощью уравнения Ван-дер-Ваальса впервые удалось описать явление перехода газа в жидкость и проанализировать критические явления.

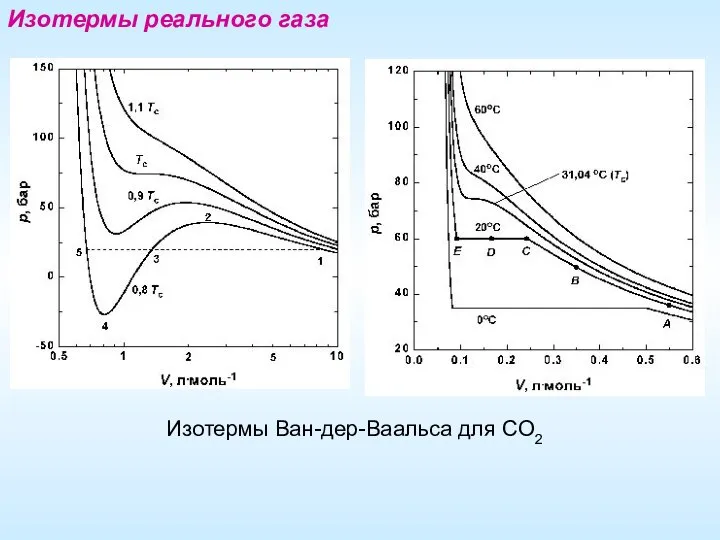
Изотермы реального газа
Изотермы Ван-дер-Ваальса для СО2

Переход жидкость–газ
Притяжение между молекулами приводит к тому, что В. назвал внутренним давлением, которое стремится удержать молекулы вместе. По мере того как объем уменьшается под действием внешнего давления, внутреннее давление возрастает гораздо быстрее внешнего. Если оно окажется равным или превысит внешнее давление, то молекулы сцепятся друг с другом и им уже не потребуется более давление со стороны содержащего их сосуда. Газ превратится в жидкость. Т.е. между газообразным и жидким состояниями нет существенной разницы. Те же самые силы и эффекты молекулярного объема действуют в обоих случаях. Различие свойств газов и жидкостей связано с различием в величине, а не в типе сил и объемных эффектов, поскольку молекулы могут располагаться ближе или дальше друг от друга.

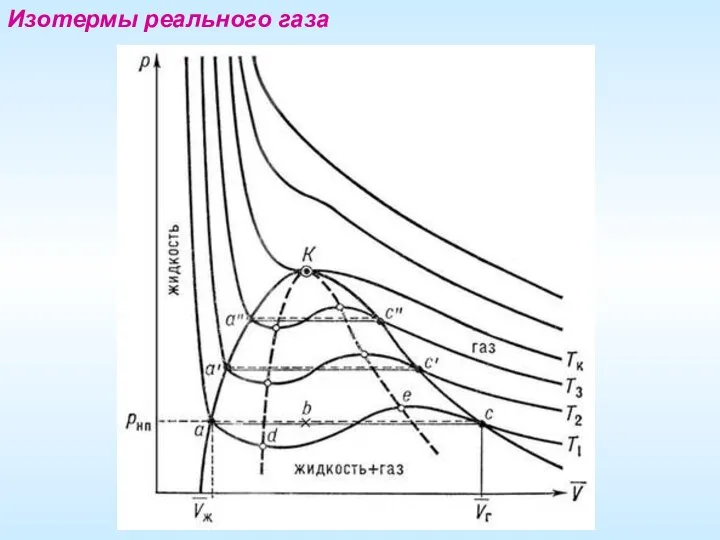
Изотермы реального газа