Определение закона движения начального звена

Тема 8

Тема 8

Тема 8
В случаях, когда установка на приводном валу маховика невозможна по конструктивным или иным соображениям, для реализации его функций можно использовать уже существующие в структуре машинного агрегата звенья, совершающие вращательные движения: ротор энергетической машины, соединительные муфты, зубчатые колеса, кулачки, шкивы, звездочки и т.п.
Основное назначение маховика состоит в ограничении колебаний угловой скорости приводного вала в пределах, определяемых заданным коэффициентом неравномерности хода.
Определение момента инерции маховика проводится в процессе проектирования машинного агрегата и составляет одну из задач его динамического синтеза.
Эффективным методом решения этой задачи является использование диаграммы Виттенбауэра. Касательные, проведенные к этой диаграмме и соответствующие допустимым для заданного коэффициента неравномерности хода значениям максимальной и минимальной угловой скорости ведущего звена, позволяют определить величину необходимого момента инерции маховика.

Тема 8

Тема 8

Тема 8

Тема 8

Тема 8

Тема 8

Тема 9
Тема 9. Уравновешивание механизмов и балансировка вращающихся масс
9.1. Виды неуравновешенности механизмов
При движении звеньев механизмов в КП возникают дополнительные динамические нагрузки от сил и моментов сил инерции звеньев. Это происходит из-за того, что центры масс звеньев в общем случае имеют переменные по величине и направлению ускорения. Так как всякий механизм имеет неподвижное звено – стойку, то и на нее, и на фундамент будут передаваться динамические нагрузки.
Переменные динамические нагрузки являются причиной неуравновешенности механизмов, вызывающей появление дополнительных сил трения в КП, напряжений и вибраций звеньев и фундамента, разрушений конструкций, шума и т. д. Поэтому при проектировании механизмов и машин ставится задача устранения неуравновешенности. Решить её можно установкой в определенных местах конструкции механизма дополнительных масс (противовесов), приводящих к ограничению динамических нагрузок.
Уравновешиванием называется полное или частичное устранение динамических нагрузок путем рационального распределения масс звеньев или подбора внешних сил, действующих на механизм.

Тема 9
Рассмотрим плоский механизм, начальное звено 1 которого вращается с постоянной угловой скоростью. Приведем всю систему сил инерции к главному вектору сил инерции Ф , приложенному в т. А, и главному моменту сил инерции МФ :
Ф
МФ
Так как w1 = const, то MФ1 = 0.
Динамические составляющие сил давления
стойки на основание численно равны общему главному
вектору и общему главному моменту сил инерции.
Уравновешенным считается механизм, у которого
главный и главный момент сил инерции равны нулю.
Если общий главный вектор сил инерции
то механизм статически неуравновешен.
Если моментная неуравновешенность.
Если динамическая неуравновешенность.

Тема 9
9.2. Неуравновешенность вращающихся масс (роторов)
На вращающиеся звенья механизма действуют переменные центробежные силы инерции из-за несимметричного расположения массы звеньев по их объему. В теории уравновешивания любое вращающееся звено называется ротором. Если вращение ротора сопровождается появлением динамических реакций и вибраций его опор и стойки, то такой ротор называется неуравновешенным.
В зависимости от взаимного расположения
оси вращения О-О ротора и главной центральной
оси инерции (ГЦОИ) I-I различают статическую
(рис. а), когда ось вращения и ГЦОИ параллельны;
моментную (рис. б), когда оси пересекаются
в центре масс ротора и динамическую (рис. в)
неуравновешенности, когда эти оси
пересекаются вне центра или перекрещиваются.
Уравновешивание роторов или вращающихся
масс используется при проектировании механизмов.

Тема 9
Из теоретической механики известно, что давление вращающегося тела на его опоры, в общем случае, складывается из двух составляющих: статической, обусловленной действием заданных сил, и динамической, определяемой ускоренным движением материальных частиц, из которых состоит вращающееся тело (ротор). У неуравновешенного ротора динамическая составляющая не равна нулю.
При равномерном вращении ротора вокруг
оси z проекции динамической составляющей
определяются следующим образом:
XA +XB = Фх; YA +YB = Фy;
– XAa +XBb = MФy; YAa – YBb = MФx.
Эти проекции главных векторов и главных
моментов сил инерции находятся по формулам:
Фx = m xs; Фy = m ys;
MФх = – Jyz; MФy = – Jxz.
Здесь m – масса ротора; Jyz, Jxz – центробежные моменты инерции ротора относительно системы координат Oxyz.

Тема 9

Тема 9

Тема 9
Для устранения малой неуравновешенности, возникающей после изготовления звеньев и их монтажа из-за несоблюдения размеров в процессе изготовления, неточности сборки, неоднородности материала, звенья подвергают балансировке. Балансировкой называется процесс уравновешивания вращающихся звеньев путем подбора и установки дополнительных масс.
Если масса ротора распределена относительно оси вращения равномерно, то ГЦОИ совпадает с осью вращения и ротор является уравновешенным.
Различают балансировку:
– статическую, которую производят для достаточно плоских роторов типа дисков, колес, маховиков, шкивов. Ротор при этом устанавливают в опорах с малым трением (например, на призмах) и путем добавления масс или высверливания добиваются безразличного положения балансируемого ротора на опорах;
– динамическую, которую выполняют для роторов, имеющих значительную длину (валы, широкие колеса, шкивы и т.д.), на специальных станках.

Тема 9
9.3. Уравновешивание механизмов
Целью уравновешивания механизмов является устранение переменных во времени и пространстве воздействий стойки механизма на основание и фундамент.
Полное уравновешивание (статическое, моментное и динамическое) рычажных механизмов является очень трудной задачей, поэтому в большинстве случаев ограничиваются их статическим уравновешиванием. Однако и его не всегда удается осуществить в полной мере. В этих случаях производится частичное статическое уравновешивание.
При статическом уравновешивании механизма необходимо обеспечить условие Ф = 0.
Так как масса системы всех подвижных звеньев то ускорение центра масс S этой должно быть равным нулю (aSM = 0). Это условие выполняется тогда, когда центр масс S системы подвижных звеньев не перемещается.
Таким образом, статическое уравновешивание есть такое действие, в результате которого центр масс системы подвижных звеньев работающего механизма становится неподвижным.

Тема 9
На практике наиболее часто применяют следующие способы статического уравновешивания.
1. Выбор симметричных схем механизмов.
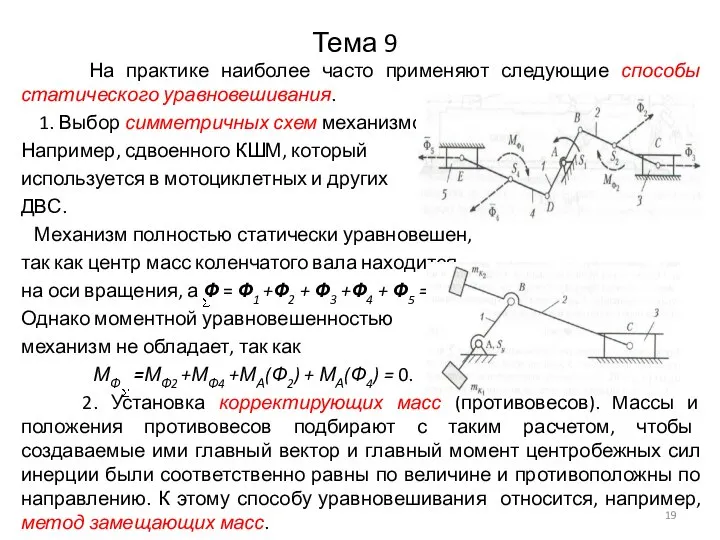
Например, сдвоенного КШМ, который
используется в мотоциклетных и других
ДВС.
Механизм полностью статически уравновешен,
так как центр масс коленчатого вала находится
на оси вращения, а Ф = Ф1 +Ф2 + Ф3 +Ф4 + Ф5 = 0.
Однако моментной уравновешенностью
механизм не обладает, так как
МФ =МФ2 +МФ4 +МА(Ф2) + МА(Ф4) = 0.
2. Установка корректирующих масс (противовесов). Массы и положения противовесов подбирают с таким расчетом, чтобы создаваемые ими главный вектор и главный момент центробежных сил инерции были соответственно равны по величине и противоположны по направлению. К этому способу уравновешивания относится, например, метод замещающих масс.

Тема 9
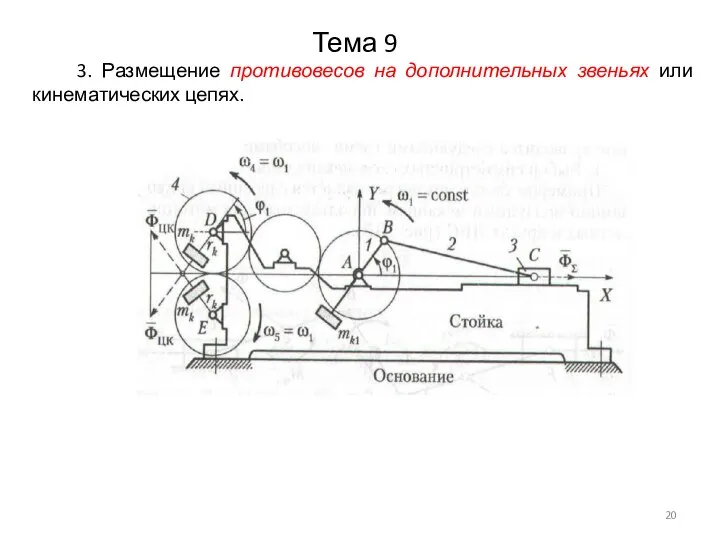
3. Размещение противовесов на дополнительных звеньях или кинематических цепях.

Тема 9
9.4. Метод замещающих масс
Этот метод состоит в следующем: каждое звено механизма заменяется двумя сосредоточенными массами, затем введением корректирующие масс (противовесов) добиваются того, чтобы центры объединенных масс оказались размещенными в неподвижных точках механизма.
При использовании этого метода звено
механизма с распределенной массой заменяется
расчетной моделью, состоящей из точечных масс.
Точки приведения масс можно выбирать
произвольно, но обычно замещающие массы
располагают в КП (шарнирах). Условия перехода:
1. Сохранение массы модели и звена:
miA + miB = mi.
2. Сохранение положения центра масс:
lASi = const; miA lASi = miB (lAB – lASi).
3. Сохранение момента инерции:
MiA l2ASi +miB(lAB – lASi)2 = Jsi.

Тема 9
Очевидно, что выполнить три условия системой с двумя массами невозможно, поэтому при статическом уравновешивании ограничиваются выполнением двух первых условий. Чтобы обеспечить выполнение всех трех условий необходимо ввести третью (корректирующую) массу.
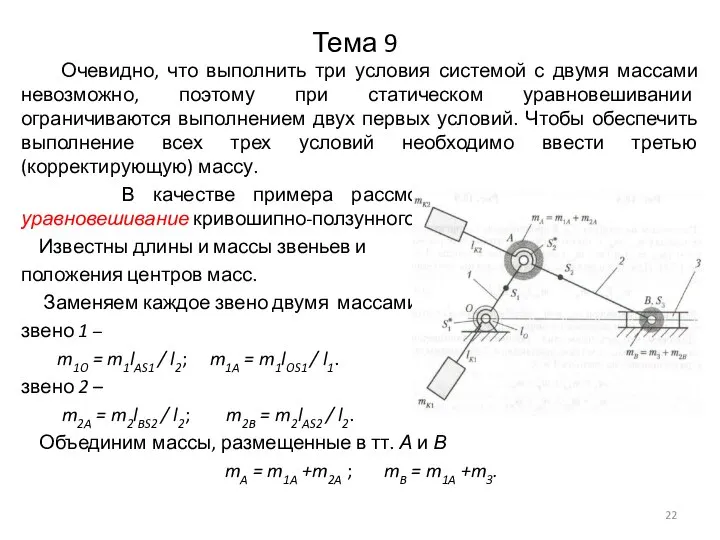
В качестве примера рассмотрим полное статическое уравновешивание кривошипно-ползунного механизма.
Известны длины и массы звеньев и
положения центров масс.
Заменяем каждое звено двумя массами:
звено 1 –
m1O = m1lAS1 / l2; m1A = m1lOS1 / l1.
звено 2 –
m2A = m2lBS2 / l2; m2B = m2lAS2 / l2.
Объединим массы, размещенные в тт. А и В
mA = m1A +m2A ; mB = m1A +m3.

Тема 9
Массу звена 3 уравновесим корректирующей массой mK2 , определяемой из соотношения mK2lK2 = mB l2 (задавшись lK2):
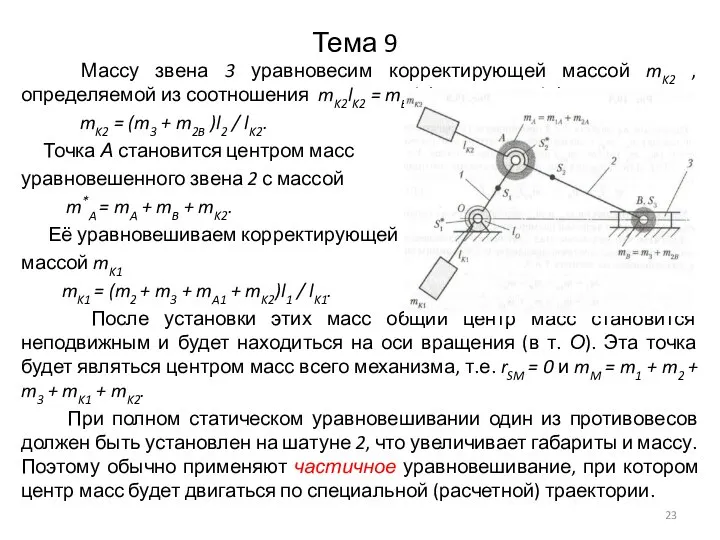
mK2 = (m3 + m2B )l2 / lK2.
Точка А становится центром масс
уравновешенного звена 2 с массой
m*A = mA + mB + mK2.
Её уравновешиваем корректирующей
массой mK1
mK1 = (m2 + m3 + mA1 + mK2)l1 / lK1.
После установки этих масс общий центр масс становится неподвижным и будет находиться на оси вращения (в т. О). Эта точка будет являться центром масс всего механизма, т.е. rSM = 0 и mM = m1 + m2 + m3 + mK1 + mK2.
При полном статическом уравновешивании один из противовесов должен быть установлен на шатуне 2, что увеличивает габариты и массу. Поэтому обычно применяют частичное уравновешивание, при котором центр масс будет двигаться по специальной (расчетной) траектории.