Содержание
- 2. Fупр mg Сила упругости – сила, возникающая при деформации тела и направленная противоположно направлению смещения частиц
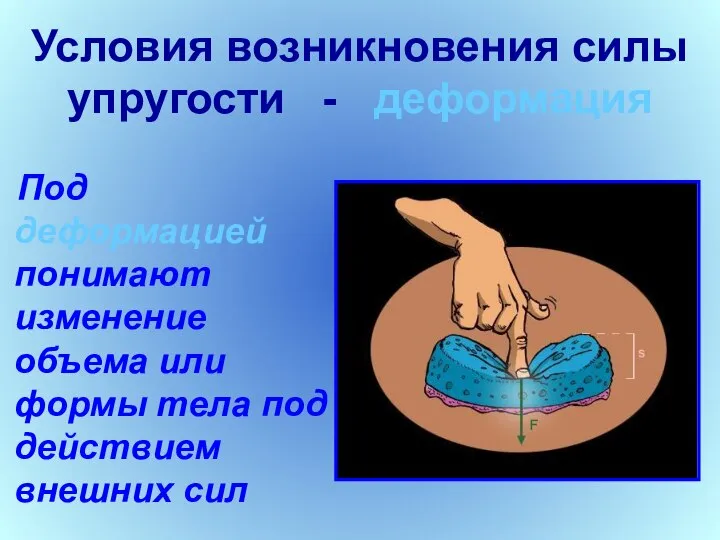
- 3. Условия возникновения силы упругости - деформация Под деформацией понимают изменение объема или формы тела под действием
- 4. Причины деформации При изменении расстояния между атомами изменяются силы взаимодействия между ними, которые стремятся вернуть тело
- 5. Виды деформаций
- 6. Основные типы упругой деформации
- 7. Основные типы упругой деформации
- 8. Основные типы упругой деформации
- 9. Основные типы упругой деформации
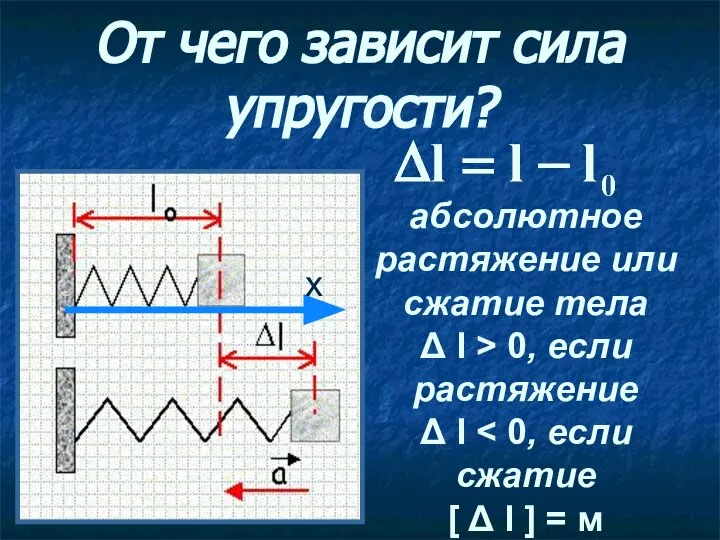
- 10. От чего зависит сила упругости? абсолютное растяжение или сжатие тела Δ l > 0, если растяжение
- 11. Сила упругости прямо пропорциональна абсолютному удлинению (растяжению) тела
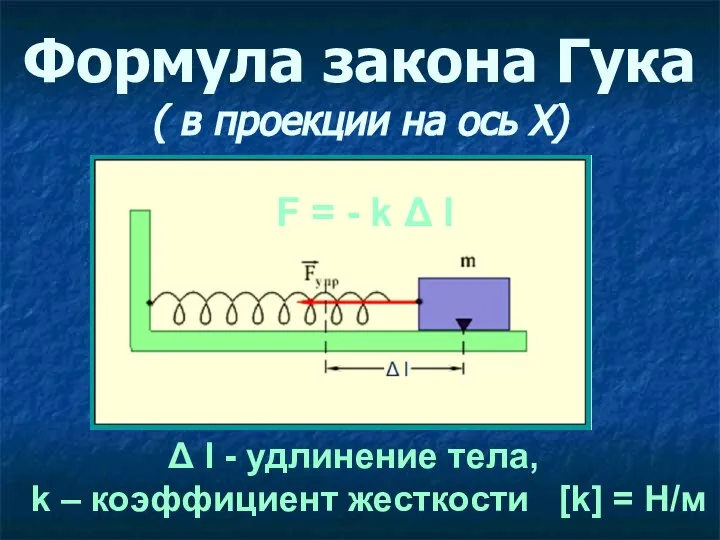
- 12. Формула закона Гука ( в проекции на ось Х) Δ l - удлинение тела, k –
- 13. Что называется жесткостью тела? Коэффициент жесткости зависит от формы и размеров тела, а также от материала.
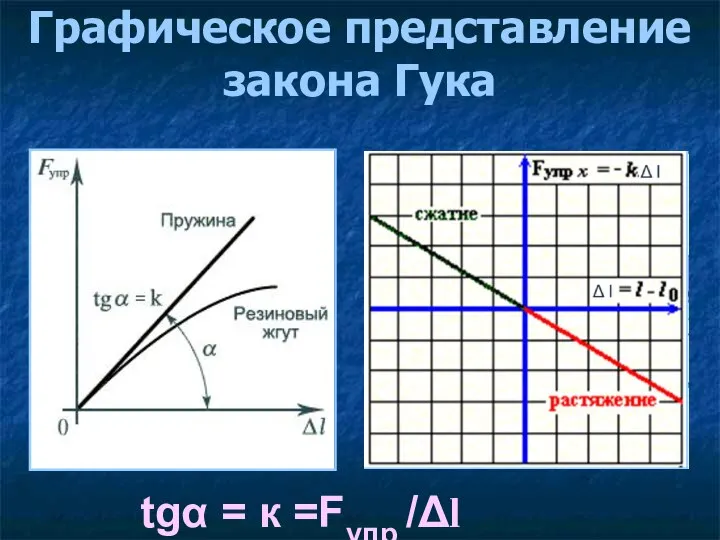
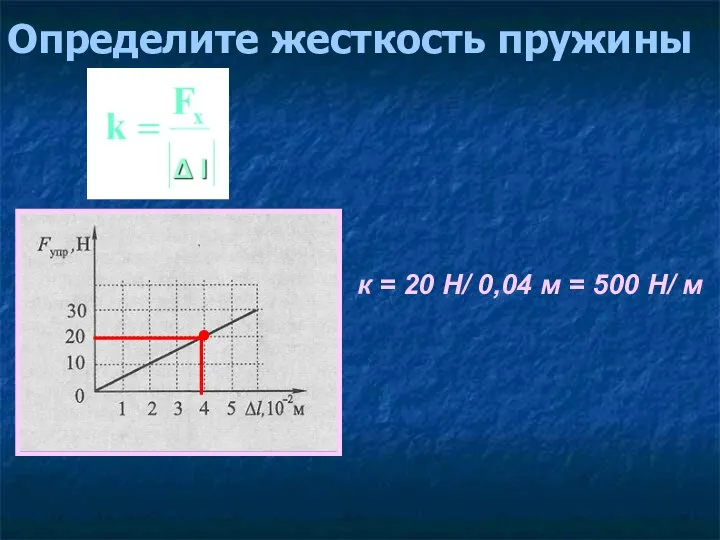
- 14. Графическое представление закона Гука tgα = к =Fупр /Δl
- 15. Определите жесткость пружины к = 20 Н/ 0,04 м = 500 Н/ м
- 16. Закон Гука для малых упругих деформаций Сила упругости, возникающая при деформации тела, прямо пропорциональна его удлинению
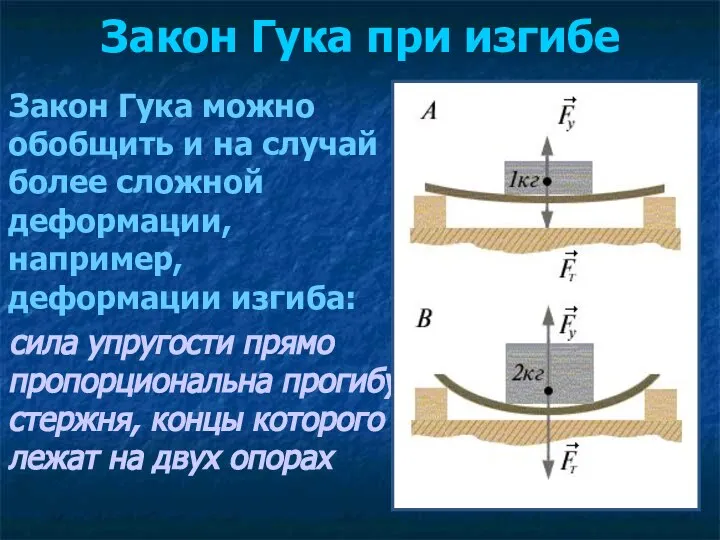
- 17. Закон Гука при изгибе Закон Гука можно обобщить и на случай более сложной деформации, например, деформации
- 18. Расчет коэффициента жесткости двух пружин (параллельное соединение) Имеем две пружины с коэффициентами жесткости к1 и к2.
- 19. Расчет коэффициента жесткости двух пружин (последовательное соединение) Имеем две пружины с коэффициентами жесткости к1 и к2.
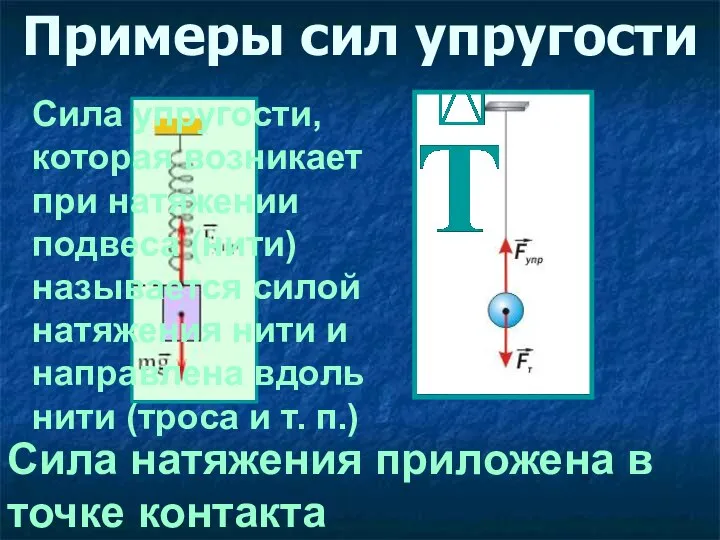
- 20. Примеры сил упругости Сила натяжения приложена в точке контакта Сила упругости, которая возникает при натяжении подвеса
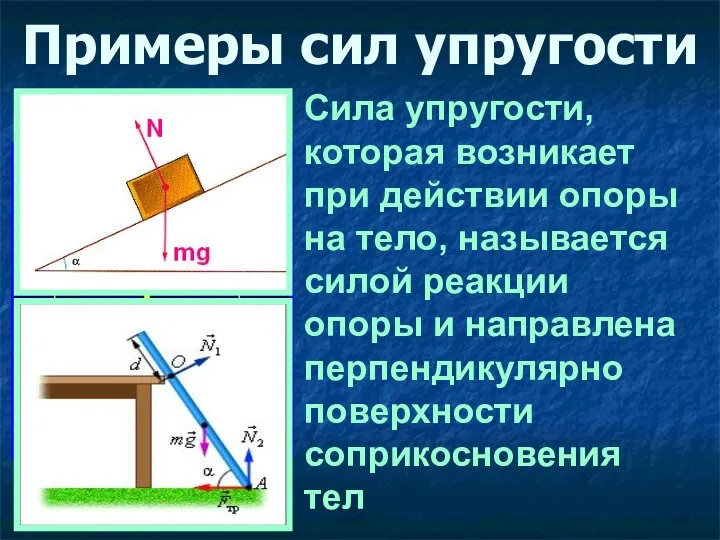
- 21. Примеры сил упругости Сила упругости, которая возникает при действии опоры на тело, называется силой реакции опоры
- 22. Когда справедлив закон Гука?
- 24. Скачать презентацию













 Энергия системы неподвижных точечных зарядов
Энергия системы неподвижных точечных зарядов 16M33┐є┐и▓ё╙═╗·┐к╖в┼р╤╡╫╩┴╧пер
16M33┐є┐и▓ё╙═╗·┐к╖в┼р╤╡╫╩┴╧пер Инерция и инертность
Инерция и инертность 9 кл Механическое дв-ние
9 кл Механическое дв-ние Оборудование для подачи воды из удалённого водоисточника
Оборудование для подачи воды из удалённого водоисточника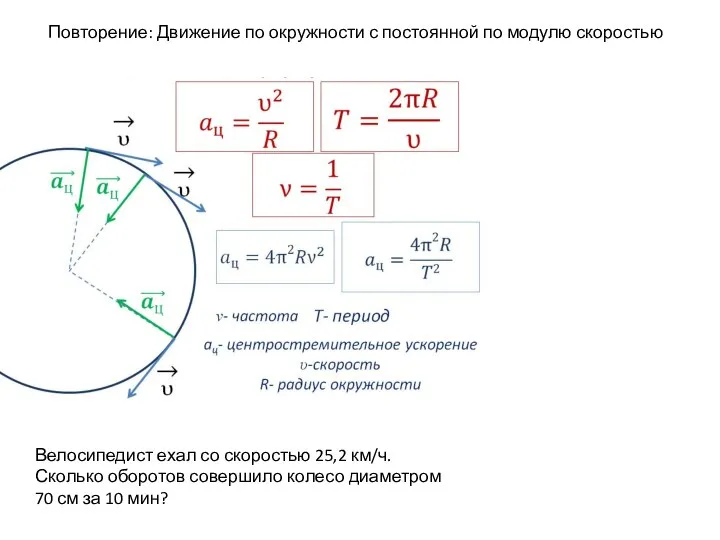 Закон всемирного тяготения
Закон всемирного тяготения Балочные системы
Балочные системы Электрический генератор
Электрический генератор Давление твёрдых тел. Давление в жидкости. Атмосферное давление
Давление твёрдых тел. Давление в жидкости. Атмосферное давление Разработка технологии установки, эксплуатации и ремонта судовых аккумуляторов
Разработка технологии установки, эксплуатации и ремонта судовых аккумуляторов Сравнительная характеристика проводниковых материалов. Медь и алюминий
Сравнительная характеристика проводниковых материалов. Медь и алюминий Выталкивающая сила
Выталкивающая сила Будова атома
Будова атома Презентация на тему Закон Паскаля
Презентация на тему Закон Паскаля  Презентация на тему Виды теплопередачи. Конвекция
Презентация на тему Виды теплопередачи. Конвекция  Резание тонколистового металла и проволоки
Резание тонколистового металла и проволоки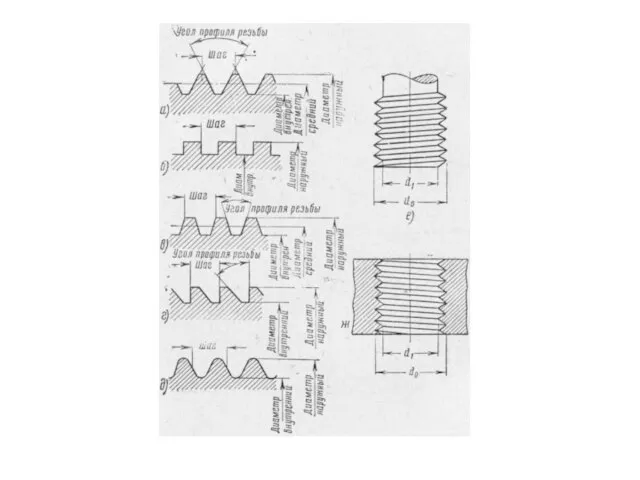 Технология обработки на металлорежущих станках. Элементы резьбы
Технология обработки на металлорежущих станках. Элементы резьбы Демонтаж рулевого управления автомобиля
Демонтаж рулевого управления автомобиля Презентация на тему Спектры . Спектральный анализ. Спектральные аппараты
Презентация на тему Спектры . Спектральный анализ. Спектральные аппараты  Газовые законы
Газовые законы Виды теплопередачи
Виды теплопередачи Деление ядра урана. Устройство и принцип действия ядерного реактора
Деление ядра урана. Устройство и принцип действия ядерного реактора Презентация на тему Линза. Построение изображения в линзе
Презентация на тему Линза. Построение изображения в линзе  Внешний фотоэффект. Изучение законов внешнего фотоэффекта
Внешний фотоэффект. Изучение законов внешнего фотоэффекта Теплоусвоение внутренних поверхностей ограждающих конструкций
Теплоусвоение внутренних поверхностей ограждающих конструкций Презентация на тему Движение тела, брошенного вертикально вверх
Презентация на тему Движение тела, брошенного вертикально вверх  Режим натуральной мощности
Режим натуральной мощности Двухтактный ДВС
Двухтактный ДВС