Математическая модель линейной динамической системы в форме проблемных матриц. Лекция #3

Математическая модель линейной системы в форме проматрицы

Далее везде нумерация формул, определений и пр.
дается в соответствии с [3].

Квадратность.
2. Невырожденность.
Эти свойства квадратности и невырожденности обеспечивают проматрице любой задачи двустороннюю обратимость, так что обратная к ней матрица всегда единственна. В основе этого важнейшего свойства проматриц лежит введенное дополнительное регуляризирующее тождество.
Автономность, т.е. все уравнения (коэффициенты исходных уравнений) представлены в проматрице самостоятельными строками-уравнениями.
Разреженность, т.е. большое количество нулевых элементов проматрицы, что может значительно облегчить выполнение вычислительных процедур.
5. Универсальность – применимость для любой формы модели, т.е. в любой задаче исследуемую или синтезируемую систему можно представить в форме обобщенного уравнения и, следовательно, соответствующей проматрицы.
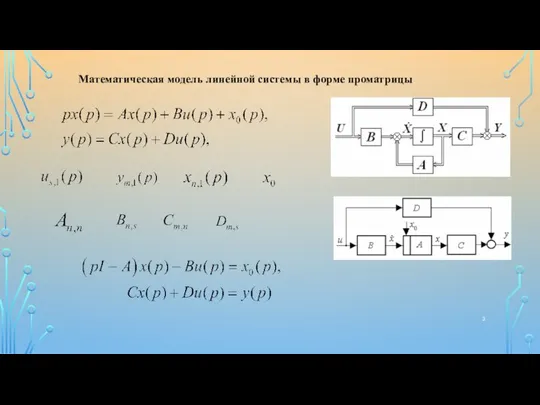
Свойства проматрицы

Продемонстрируем свойство универсальности
Пусть имеется запись системы в форме левой факторизации
Дополним его формальным регуляризирующим тождеством
.
Определение 3.5. Блочная матрица называется проматрицей задачи моделирования для объекта, заданного в форме левой факторизации парой полиномиальных матриц.

Для случая правой факторизации можно по записать
Определение 3.6. Блочная матрица называется проматрицей задачи моделирования для объекта, заданного в форме правой факторизации парой полиномиальных матриц .

Проматрицы типовых соединений систем
При использовании описаний систем в пространстве состояний