N или др.) в строго зафиксированном месте сооружения при движении по нем груза Р=1.
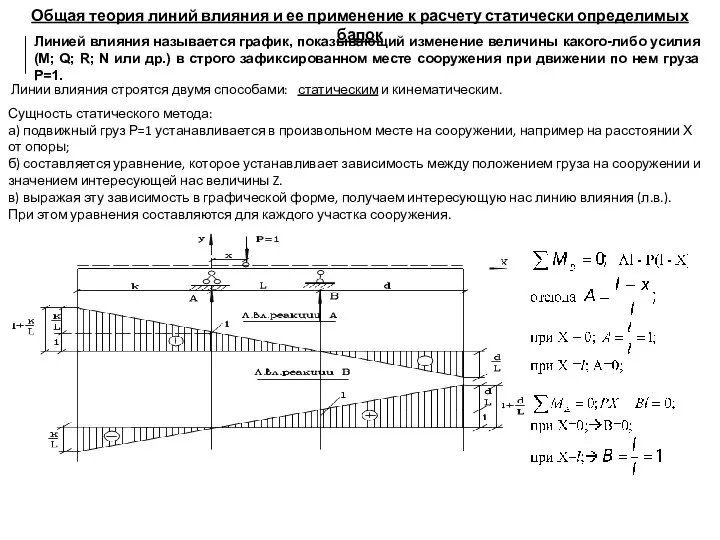
Общая теория линий влияния и ее применение к расчету статически определимых балок
Линии влияния строятся двумя способами: статическим и кинематическим.
Сущность статического метода:
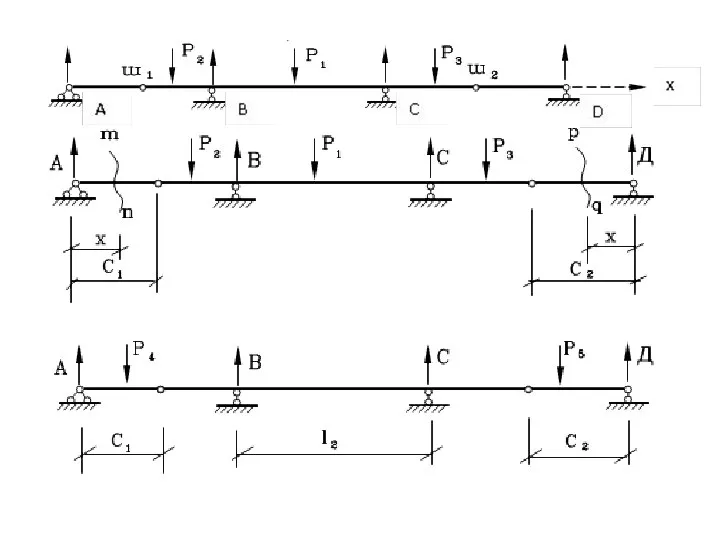
а) подвижный груз Р=1 устанавливается в произвольном месте на сооружении, например на расстоянии Х от опоры;
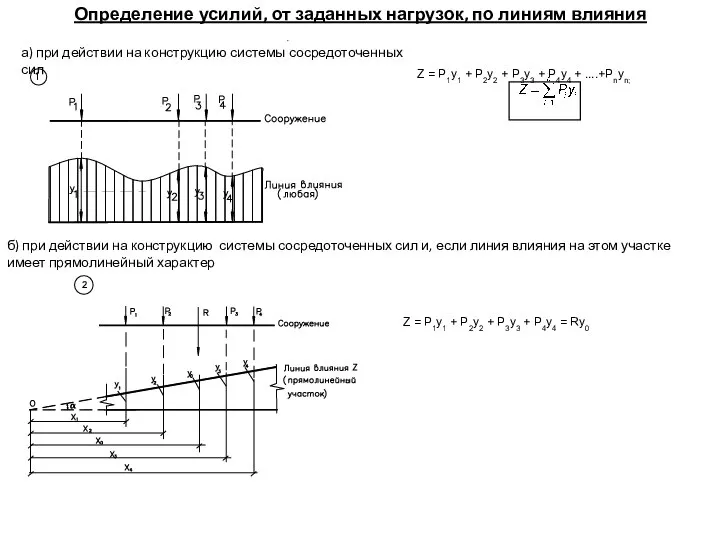
б) составляется уравнение, которое устанавливает зависимость между положением груза на сооружении и значением интересующей нас величины Z.
в) выражая эту зависимость в графической форме, получаем интересующую нас линию влияния (л.в.).
При этом уравнения составляются для каждого участка сооружения.





 Электрический ток в вакууме
Электрический ток в вакууме ЯМР спектроскопия
ЯМР спектроскопия Проект Электромагнитный двигатель из батарейки
Проект Электромагнитный двигатель из батарейки КР
КР Физические свойства пористого кремния
Физические свойства пористого кремния Презентация на тему Графическое представление газовых процессов
Презентация на тему Графическое представление газовых процессов  Состав ядра атома. Энергия связи атомных ядер. Дефект масс
Состав ядра атома. Энергия связи атомных ядер. Дефект масс Электрическое поле. Однородное и неоднородное электрическое поле. Напряженность электрического поля
Электрическое поле. Однородное и неоднородное электрическое поле. Напряженность электрического поля Дробилка безрешетная
Дробилка безрешетная Конструкция. Движетель
Конструкция. Движетель Электричество. 8 класс
Электричество. 8 класс Презентация на тему П.А. Сорокин. Флуктуация
Презентация на тему П.А. Сорокин. Флуктуация  Силы в механике
Силы в механике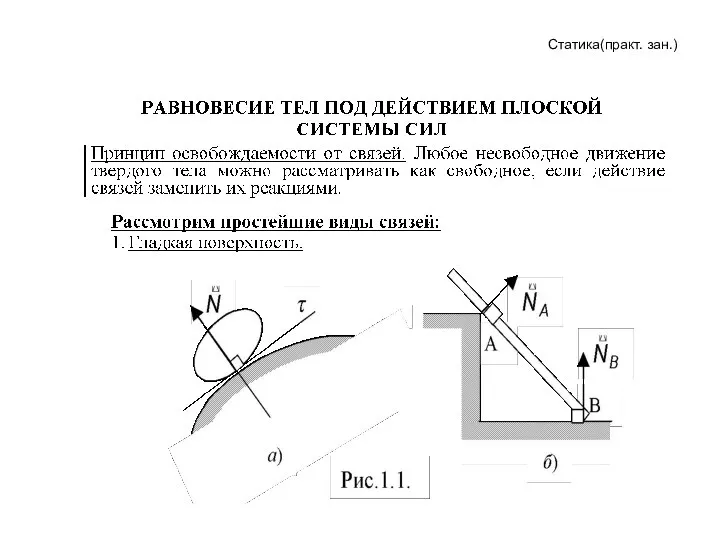 Равновесие тел под действием плоской системы сил
Равновесие тел под действием плоской системы сил Хот-роды
Хот-роды Термодинамические циклы. Второе начало термодинамики. Энтропия. Термодинамические потенциалы
Термодинамические циклы. Второе начало термодинамики. Энтропия. Термодинамические потенциалы Гидростатика. Сила давления
Гидростатика. Сила давления Электромагнитные взаимодействия ядер
Электромагнитные взаимодействия ядер Термодинамические функции газовых смесей. Идеальные растворы. Закон Рауля
Термодинамические функции газовых смесей. Идеальные растворы. Закон Рауля etalon_otredaktirovana_LEKTsIYa_8_ioniziruyuschee_ETALON
etalon_otredaktirovana_LEKTsIYa_8_ioniziruyuschee_ETALON Магнитное поле
Магнитное поле Использование элементов развивающего обучения на уроках физики по сингапурской системе обучения
Использование элементов развивающего обучения на уроках физики по сингапурской системе обучения Soy sauce optics
Soy sauce optics Виды, структура и утилизация батареек
Виды, структура и утилизация батареек Презентация на тему Коэффициент мощности и К.П.Д. выпрямителей
Презентация на тему Коэффициент мощности и К.П.Д. выпрямителей  Построение станочного зацепления
Построение станочного зацепления Атомные спектры
Атомные спектры Презентация на тему Звуковые волны
Презентация на тему Звуковые волны