Содержание
- 2. 6.1 Установившиеся и переходные процессы. Законы коммутации 6 Переходные процессы
- 3. Установившейся режим Установившимся режимом называется такой режим, при котором токи и напряжения в цепи являются постоянными
- 4. Переходный процесс Переходным процессом называется режим, при котором токи и напряжения в цепи изменяются от одних
- 5. Причины переходных процессов При изменении действующих в электрической цепи задающих функций источников питания При изменении параметров
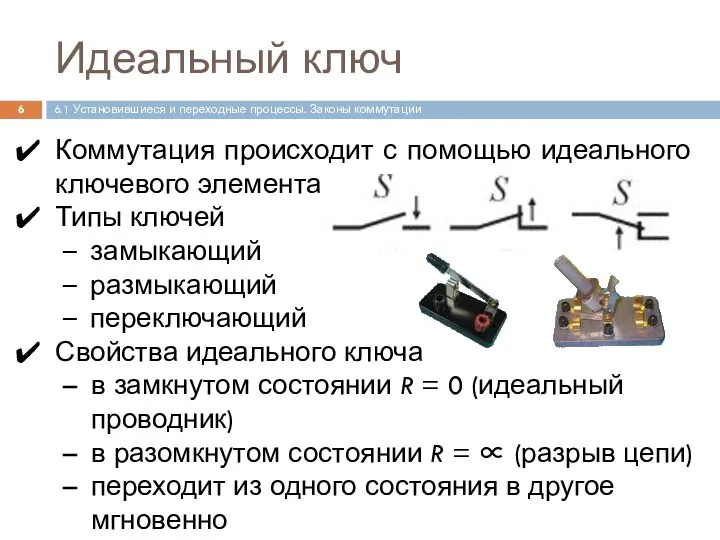
- 6. Коммутация происходит с помощью идеального ключевого элемента Типы ключей замыкающий размыкающий переключающий Свойства идеального ключа в
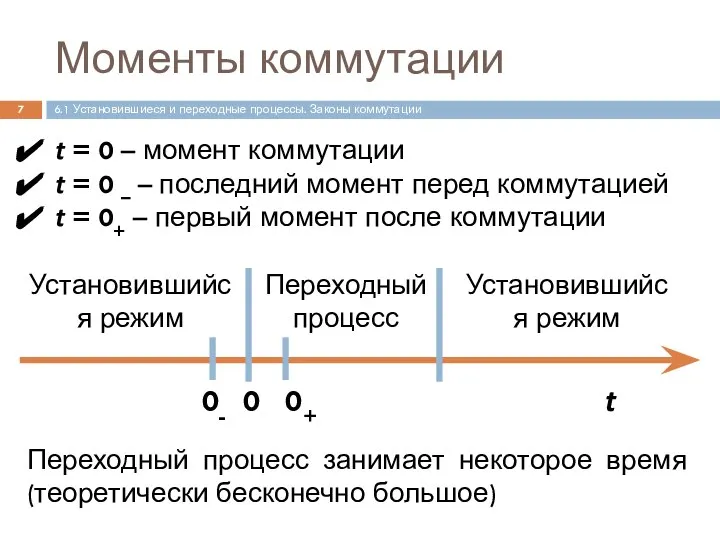
- 7. t = 0 – момент коммутации t = 0 – – последний момент перед коммутацией t
- 8. Энергия в электрической цепи Установившийся режим характеризуется определенным запасом энергии магнитного и электрического полей ik –
- 9. Законы коммутации Ток в любом индуктивном элементе является непрерывной функцией времени и не может изменяться скачком
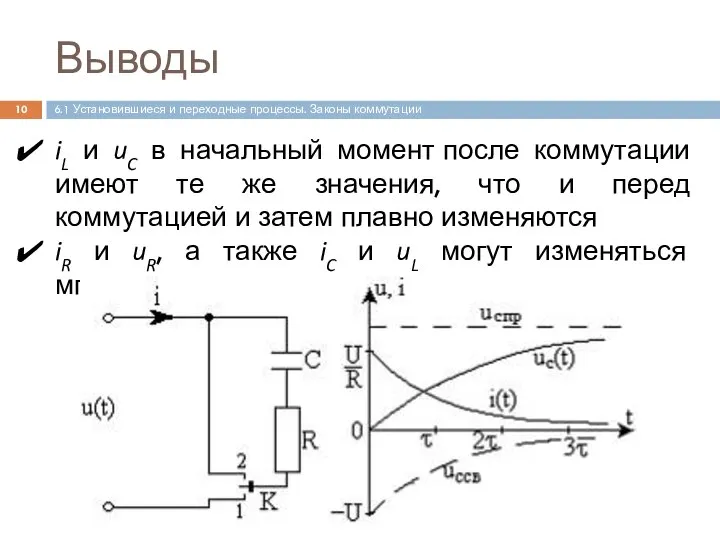
- 10. Выводы iL и uC в начальный момент после коммутации имеют те же значения, что и перед
- 11. 6.2 Общий подход к анализу переходных процессов 6 Переходные процессы
- 12. Анализ переходных процессов Задача заключается в определении мгновенных значений токов и напряжений в любой момент после
- 13. Решение задачи Определение начальных условий из законов коммутации Решение дифференциального уравнения классическим методом операторным методом 6.2
- 14. 6.2 Общий подход к анализу переходных процессов 6.2.1 Классический метод анализа 6 Переходные процессы
- 15. Суть метода Метод основан на составлении системы дифференциальных и алгебраических уравнений с использованием уравнений для элементов
- 16. Вид решения ЛДУ yСВ(t) – свободная или собственная составляющая – это общее решение соответствующего однородного ДУ
- 17. Свободная составляющая определяется свойствами самой цепи существует во время переходного процесса yСВ(t) → 0 при t
- 18. Принужденная составляющая вид частного решения определяется видом воздействия если f(t) = const, то yПР(t) = const
- 19. Этапы расчета Анализ цепи до коммутации Определяются токи через индуктивности и напряжения на емкостях в последний
- 20. Этапы расчета (продолжение) Определение свободной составляющей По дифференциальному уравнению цепи определяется характеристическое уравнение, находятся корни этого
- 21. 6.2 Общий подход к анализу переходных процессов 6.2.1 Классический метод анализа 6.2.2 Переходные процессы в RL-цепи
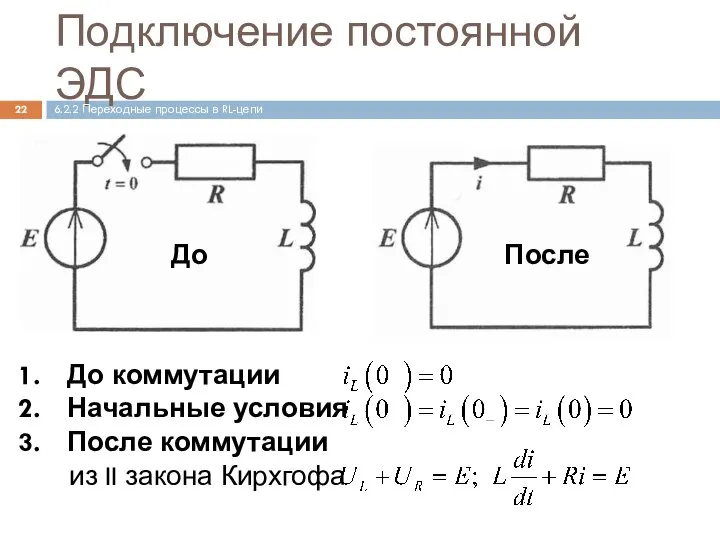
- 22. Подключение постоянной ЭДС До коммутации Начальные условия После коммутации из II закона Кирхгофа 6.2.2 Переходные процессы
- 23. Анализ RL-цепи (продолжение) Определение свободной составляющей Характеристическое уравнение Корень Постоянная времени – это время, в течение
- 24. Анализ RL-цепи (продолжение) Определение принужденной составляющей Анализ режима по постоянному току для установившегося режима после коммутации
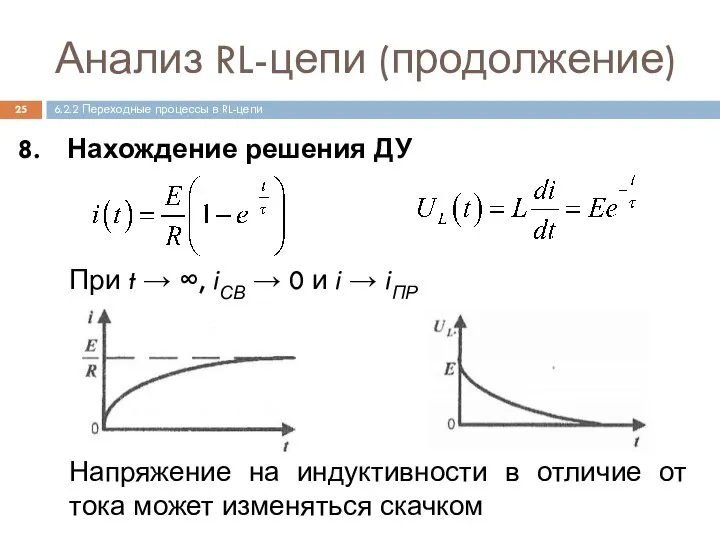
- 25. Анализ RL-цепи (продолжение) Нахождение решения ДУ 6.2.2 Переходные процессы в RL-цепи При t → ∞, iСВ
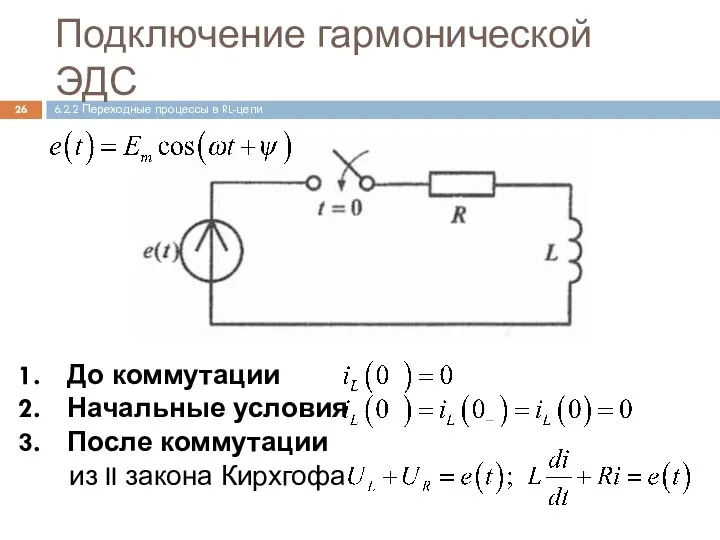
- 26. Подключение гармонической ЭДС До коммутации Начальные условия После коммутации из II закона Кирхгофа 6.2.2 Переходные процессы
- 27. Анализ RL-цепи (продолжение) Определение свободной составляющей Характеристическое уравнение Корень Определение принужденной составляющей Используется метод комплексных амплитуд
- 28. Анализ RL-цепи (продолжение) Запись общего вида решения ДУ Определение постоянных интегрирования 6.2.2 Переходные процессы в RL-цепи
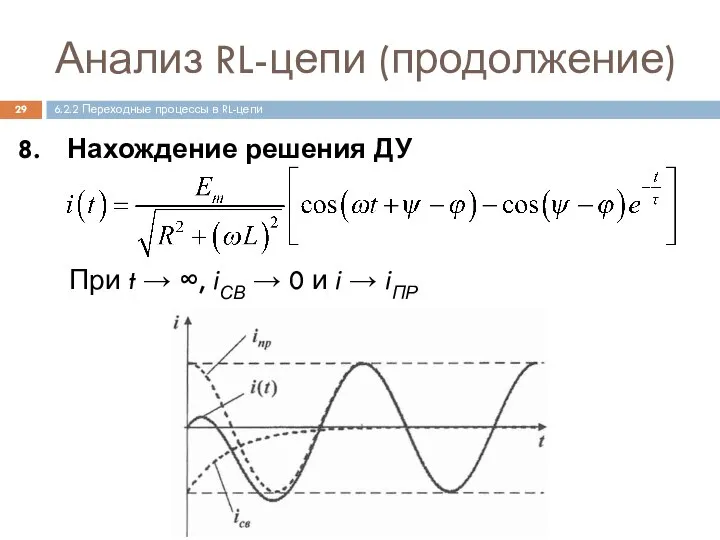
- 29. Анализ RL-цепи (продолжение) Нахождение решения ДУ 6.2.2 Переходные процессы в RL-цепи При t → ∞, iСВ
- 30. 6.2 Общий подход к анализу переходных процессов 6.2.1 Классический метод анализа 6.2.2 Переходные процессы в RL-цепи
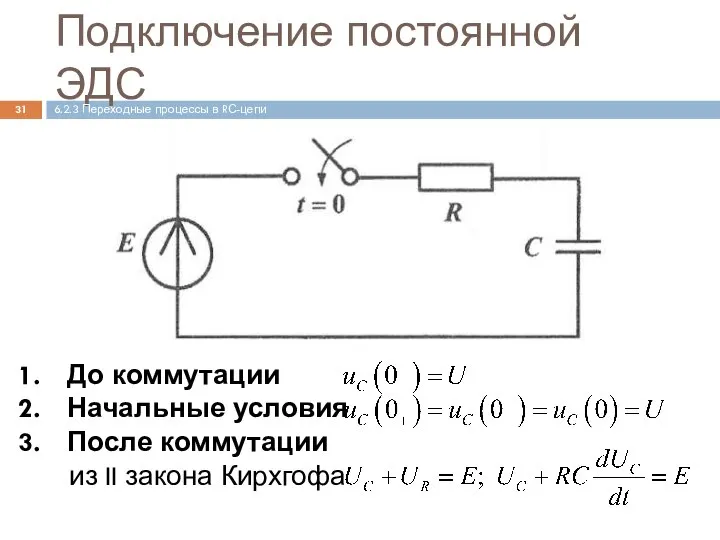
- 31. Подключение постоянной ЭДС До коммутации Начальные условия После коммутации из II закона Кирхгофа 6.2.3 Переходные процессы
- 32. Анализ RС-цепи (продолжение) Определение свободной составляющей Характеристическое уравнение Корень Определение принужденной составляющей Анализ режима по постоянному
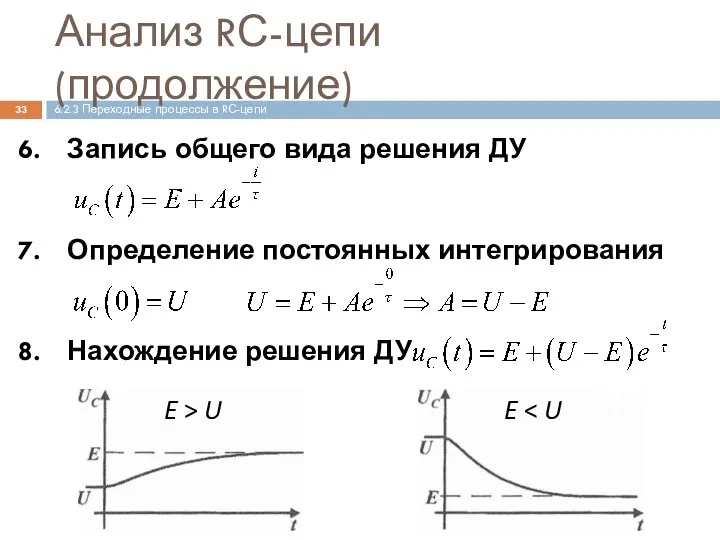
- 33. Анализ RС-цепи (продолжение) Запись общего вида решения ДУ Определение постоянных интегрирования Нахождение решения ДУ E >
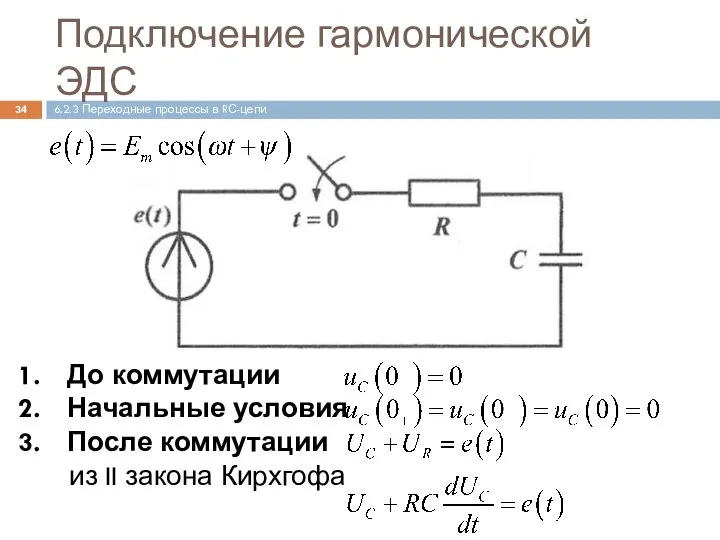
- 34. Подключение гармонической ЭДС До коммутации Начальные условия После коммутации из II закона Кирхгофа 6.2.3 Переходные процессы
- 35. Анализ RС-цепи (продолжение) Определение свободной составляющей Характеристическое уравнение Корень Определение принужденной составляющей Используется метод комплексных амплитуд
- 36. Анализ RС-цепи (продолжение) Запись общего вида решения ДУ Определение постоянных интегрирования 6.2.3 Переходные процессы в RС-цепи
- 37. Анализ RС-цепи (продолжение) Нахождение решения ДУ 6.2.3 Переходные процессы в RС-цепи
- 38. 6.2 Общий подход к анализу переходных процессов 6.2.1 Классический метод анализа 6.2.2 Переходные процессы в RL-цепи
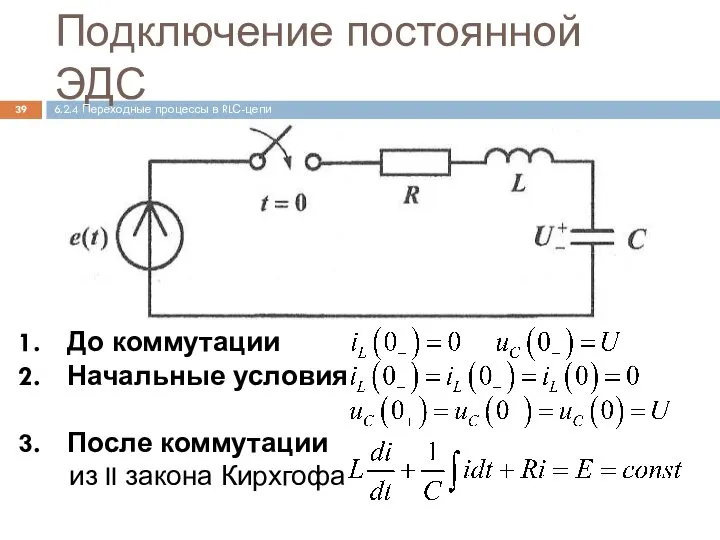
- 39. Подключение постоянной ЭДС До коммутации Начальные условия После коммутации из II закона Кирхгофа 6.2.4 Переходные процессы
- 40. Анализ RLС-цепи (продолжение) Определение свободной составляющей Характеристическое уравнение Корни или где частота резонанса 6.2.4 Переходные процессы
- 41. Анализ RLС-цепи (продолжение) Определение принужденной составляющей Анализ режима по постоянному току для установившегося режима после коммутации
- 42. Анализ RLС-цепи (продолжение) Определение постоянных интегрирования т.к. 6.2.4 Переходные процессы в RLС-цепи
- 43. Анализ RLС-цепи (продолжение) Нахождение решения ДУ Апериодический (δ > ω0, p1и p2 ∈ R) Критический (δ
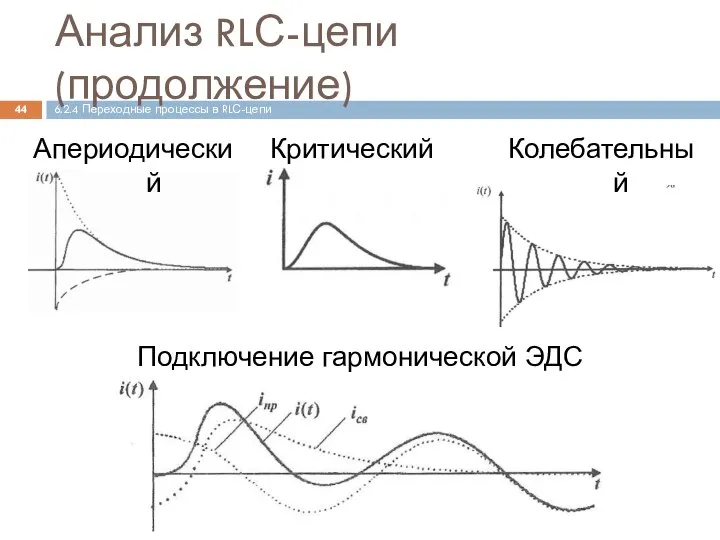
- 44. Анализ RLС-цепи (продолжение) 6.2.4 Переходные процессы в RLС-цепи Апериодический Критический Колебательный Подключение гармонической ЭДС
- 45. 6.2 Общий подход к анализу переходных процессов 6.2.5 Операторный метод анализа 6 Переходные процессы
- 46. Прямое преобразование A(p) – операторное изображение функции a(t) k и σ0 – вещественные числа Обратное преобразование
- 47. Свойство линейности Теорема дифференцирования Теорема интегрирования Теорема смещения Свойства преобразования Лапласа 6.2.5 Операторный метод анализа Теорема
- 48. Предельные соотношения Теорема разложения pk – простые корни знаменателя Свойства преобразования Лапласа 6.2.5 Операторный метод анализа
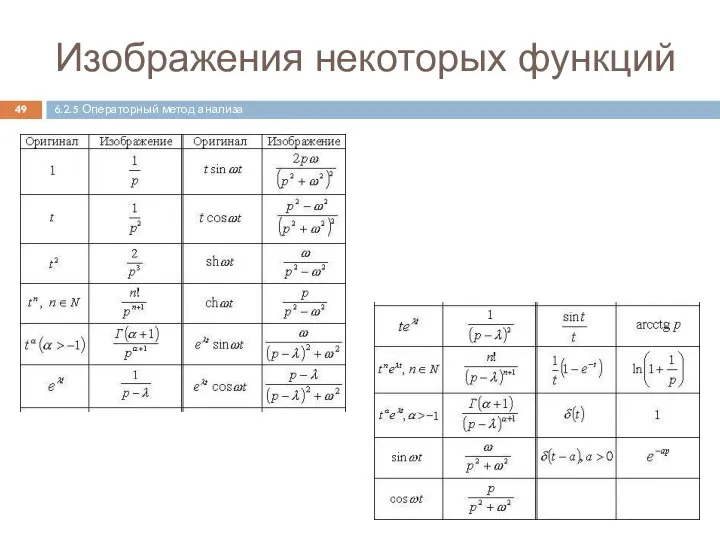
- 49. Изображения некоторых функций 6.2.5 Операторный метод анализа
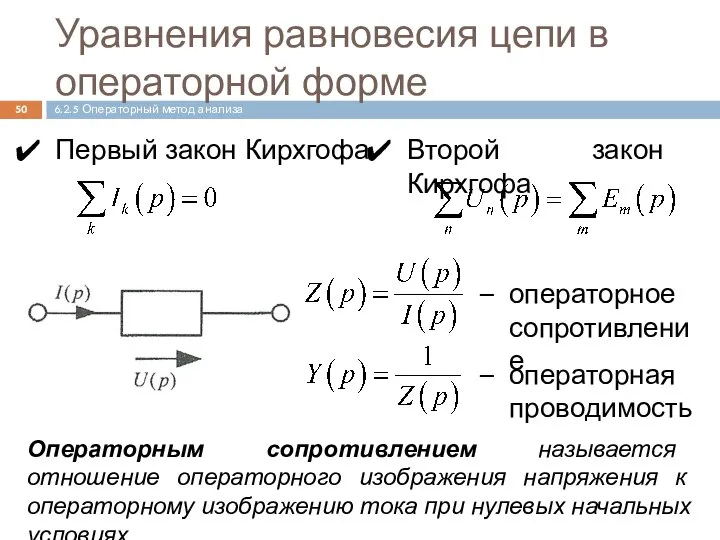
- 50. Первый закон Кирхгофа Уравнения равновесия цепи в операторной форме 6.2.5 Операторный метод анализа Второй закон Кирхгофа
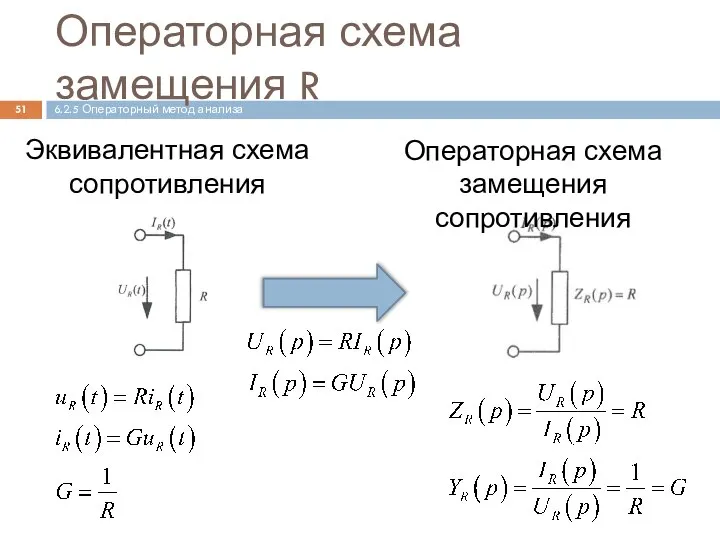
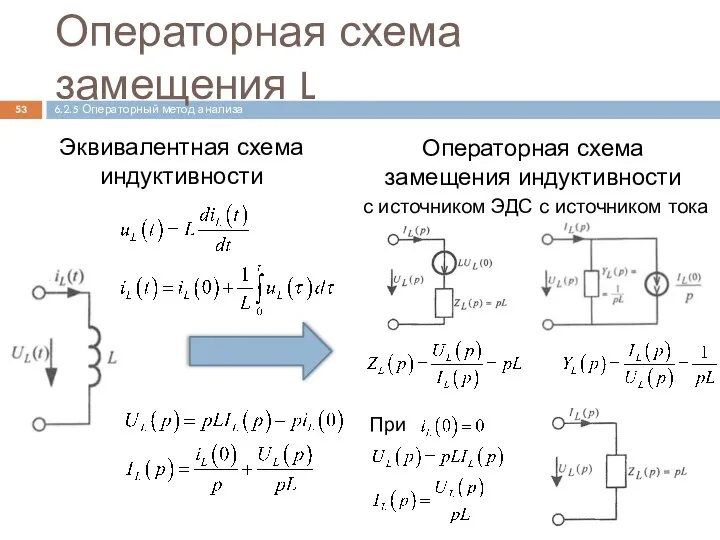
- 51. Операторная схема замещения R 6.2.5 Операторный метод анализа Эквивалентная схема сопротивления Операторная схема замещения сопротивления
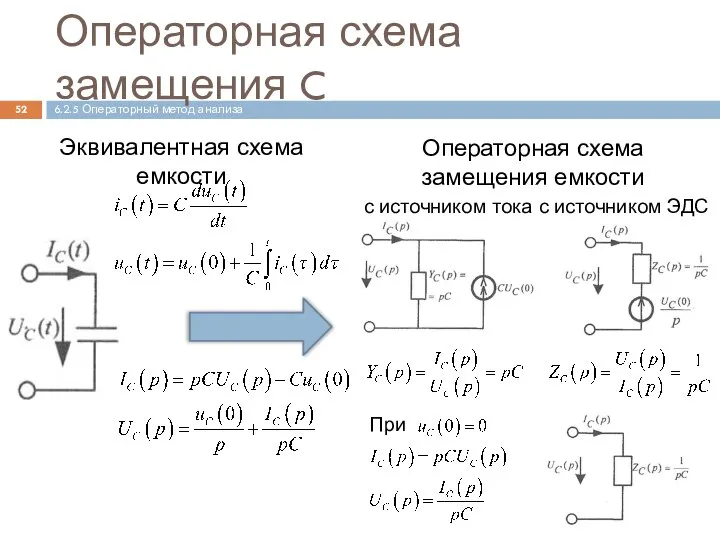
- 52. Операторная схема замещения C 6.2.5 Операторный метод анализа Эквивалентная схема емкости Операторная схема замещения емкости с
- 53. Операторная схема замещения L 6.2.5 Операторный метод анализа При Операторная схема замещения индуктивности с источником тока
- 54. Схема применения метода Анализ цепи до коммутации. Определение независимых начальных условий Составление операторной эквивалентной схемы электрической
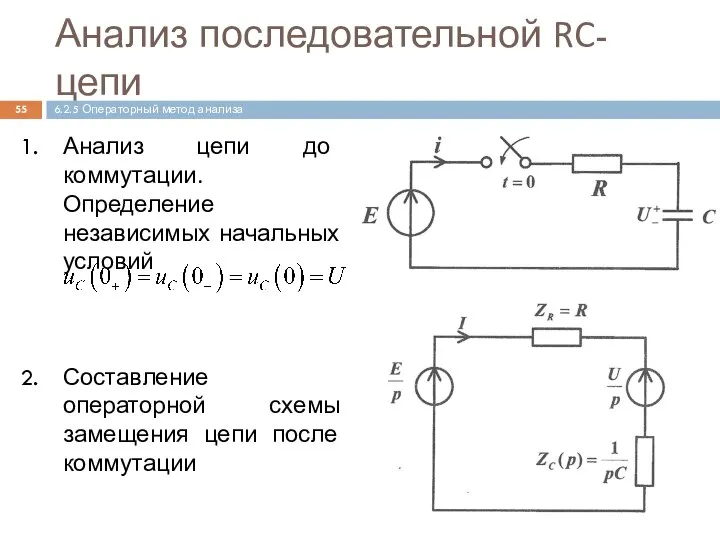
- 55. Анализ последовательной RC-цепи Анализ цепи до коммутации. Определение независимых начальных условий Составление операторной схемы замещения цепи
- 56. Анализ RС-цепи (продолжение) Запись уравнения электрического равновесия цепи в операторной форме Решение уравнения Определение оригинала 6.2.5
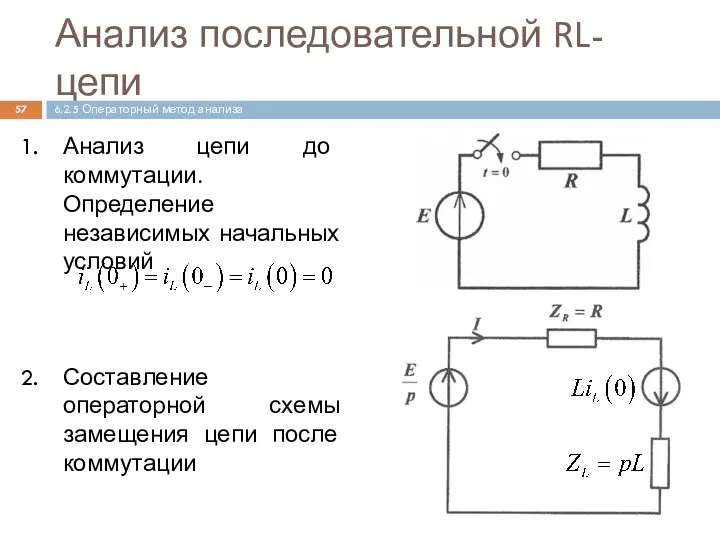
- 57. Анализ последовательной RL-цепи Анализ цепи до коммутации. Определение независимых начальных условий Составление операторной схемы замещения цепи
- 58. Анализ RL-цепи (продолжение) Запись уравнения электрического равновесия цепи в операторной форме Решение уравнения Определение оригинала 6.2.5
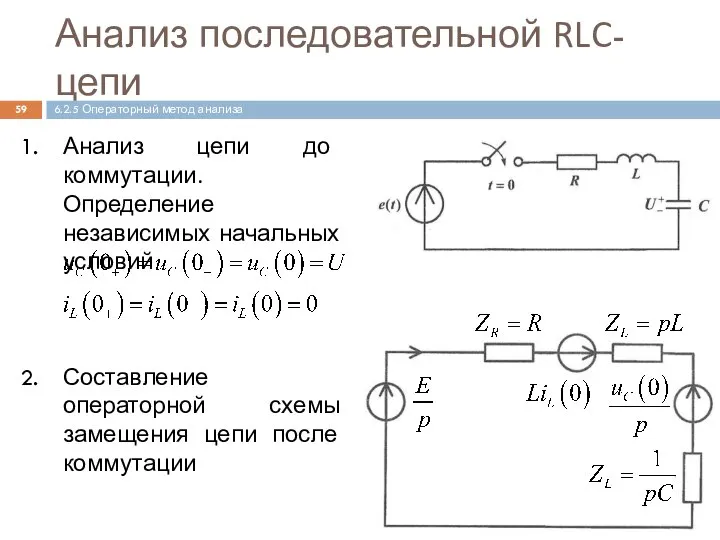
- 59. Анализ последовательной RLC-цепи Анализ цепи до коммутации. Определение независимых начальных условий Составление операторной схемы замещения цепи
- 60. Анализ RLС-цепи (продолжение) Запись уравнения электрического равновесия цепи в операторной форме Решение уравнения 6.2.5 Операторный метод
- 61. Определение оригинала Апериодический (δ > ω0, p1и p2 ∈ R) Критический (δ = ω0, p1= p2
- 62. Эквивалентные операторные схемы Источники тока и напряжений i(t) и u(t) заменяются соответствующими изображениями I(p) и U(p)
- 63. Преимущества простота отсутствие громоздких операций по определению постоянных интегрирования можно рассчитать переходный процесс любым из ранее
- 64. Операторные характеристики Операторной характеристикой линейной электрической цепи называется отношение операторного изображения реакции цепи к операторному изображению
- 65. Виды операторных характеристик Операторный коэффициент передачи по напряжению Операторный коэффициент передачи по току Операторное сопротивление Операторная
- 66. Любая операторная характеристика линейной электрической цепи, не содержащей независимых источников энергии, является рациональной функцией переменной р
- 67. Полюсно-нулевая диаграмма 6.2.5 Операторный метод анализа воздействие реакция Нули и полюса характеризуют Hnm(p) с точностью до
- 68. 6.2 Общий подход к анализу переходных процессов 6.2.6 Метод наложения (интегралы наложения) 6 Переходные процессы
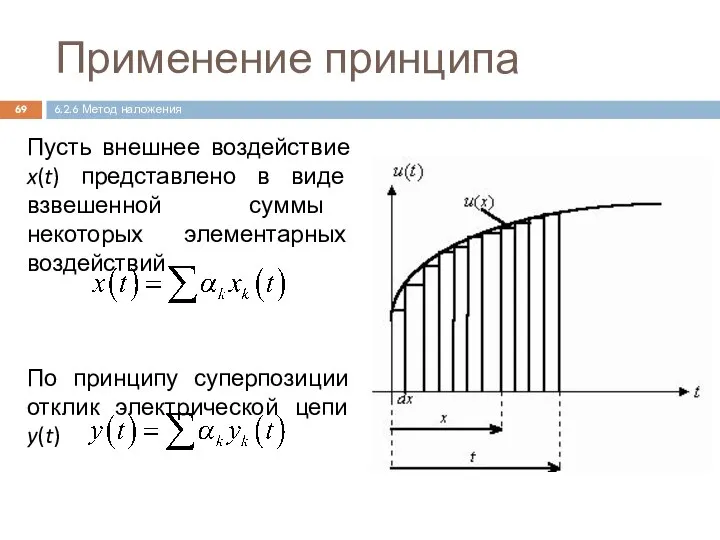
- 69. Пусть внешнее воздействие x(t) представлено в виде взвешенной суммы некоторых элементарных воздействий По принципу суперпозиции отклик
- 70. При исследовании динамических свойств линейных цепей в качестве типовых элементарных воздействий используется единичная ступенчатая функция 1(t)
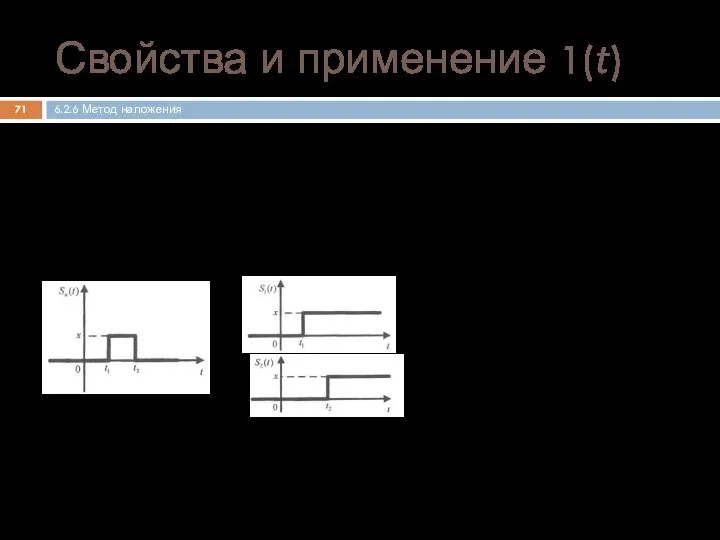
- 71. Коммутация электрических цепей Представление прямоугольного импульса Преобразование Лапласа Свойства и применение 1(t) 6.2.6 Метод наложения
- 72. Переходной характеристикой h1(t-t0) линейной цепи, не содержащей независимых источников энергии, называется отношение реакции этой цепи на
- 73. Переходная характеристика 6.2.6 Метод наложения воздействие на цепь реакция цепи При операторная характеристика цепи
- 74. Составление операторной схемы замещения цепи для нулевых начальных условий Нахождение операторной характеристики H(p) Определение переходной характеристики
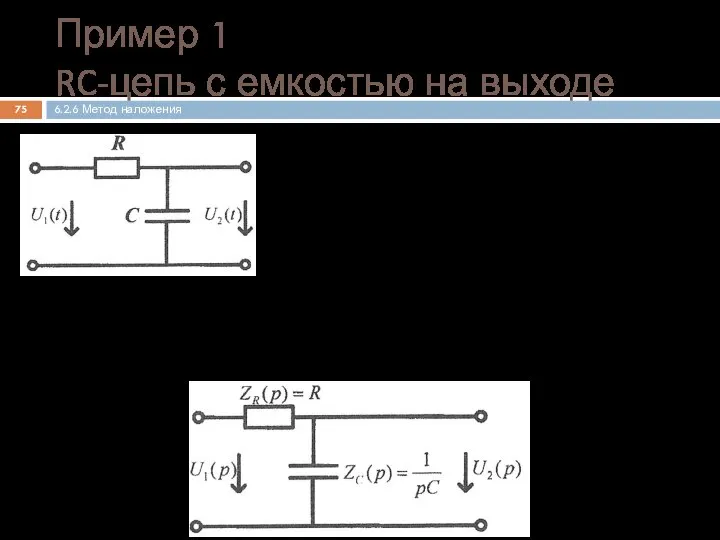
- 75. Составление операторной схемы замещения цепи для нулевых начальных условий Пример 1 RC-цепь с емкостью на выходе
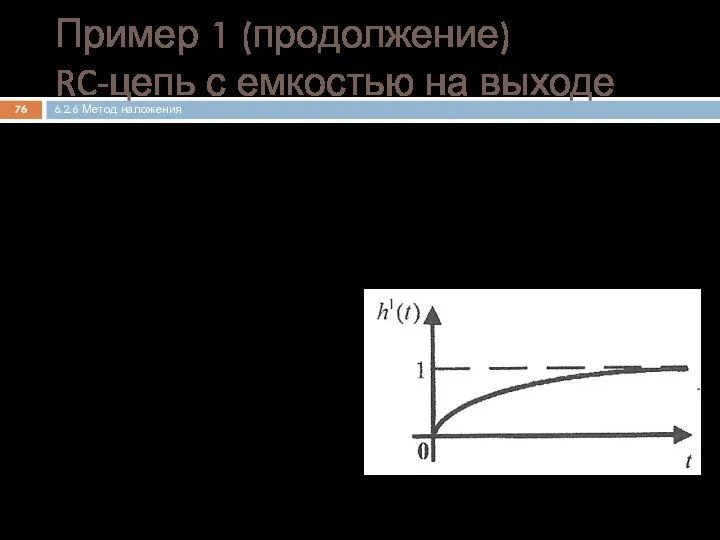
- 76. Нахождение операторного коэффициента передачи по напряжению Определение переходной характеристики Пример 1 (продолжение) RC-цепь с емкостью на
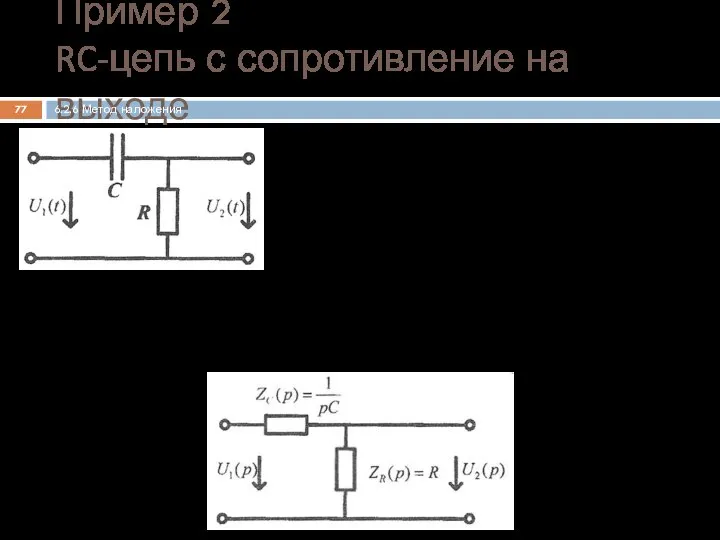
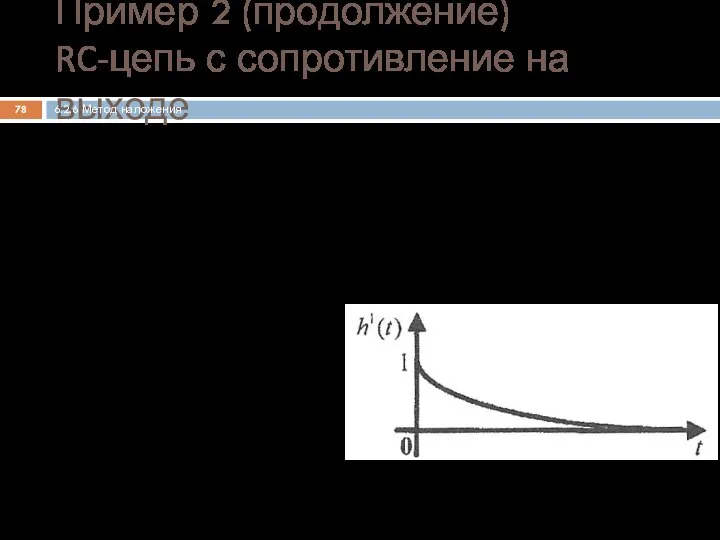
- 77. Составление операторной схемы замещения цепи для нулевых начальных условий Пример 2 RC-цепь с сопротивление на выходе
- 78. Нахождение операторного коэффициента передачи по напряжению Определение переходной характеристики Пример 2 (продолжение) RC-цепь с сопротивление на
- 79. Интеграл Дюамеля 6.2.6 Метод наложения Интеграл Дюамеля — метод расчета отклика линейных пассивных систем на произвольно
- 80. Интеграл Дюамеля (продолжение) 6.2.6 Метод наложения Отклик системы выражается в виде интеграла от произведения задержанной переходной
- 81. Импульсной характеристикой цепи называют реакцию цепи на воздействие единичной импульсной функции (δ-функции) Импульсная характеристика 6.2.6 Метод
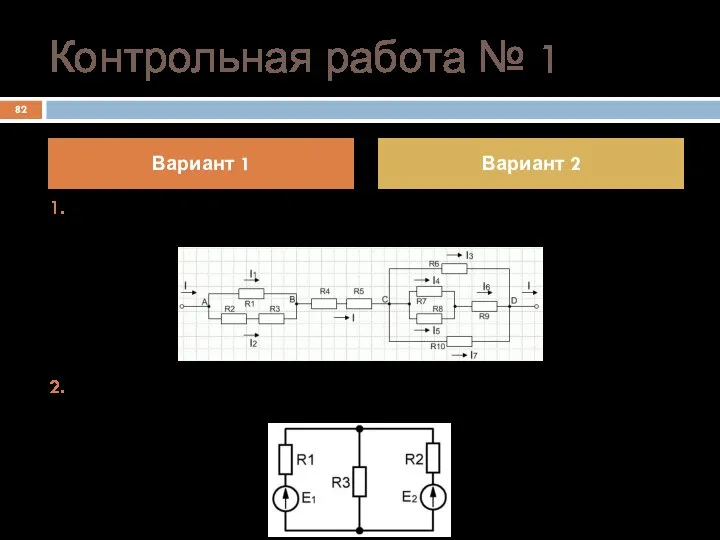
- 82. Контрольная работа № 1 Найти эквивалентное сопротивление между узлами A и D , а также определить
- 84. Скачать презентацию



















































 Сила трения
Сила трения Профилактика отечественного котла после 5 лет эксплуатации
Профилактика отечественного котла после 5 лет эксплуатации Движение и его относительность
Движение и его относительность Электроосветительные установки
Электроосветительные установки История происхождения физических терминов (работа, масса, сила, равномерное прямолинейное движение)
История происхождения физических терминов (работа, масса, сила, равномерное прямолинейное движение) Кинематика
Кинематика Подготовка к ЕГЭ на уроках физики
Подготовка к ЕГЭ на уроках физики Горение свечи. Лабораторная работа
Горение свечи. Лабораторная работа Вещества. Науки о природе
Вещества. Науки о природе Некогерентность рассеяния. (Тема 15)
Некогерентность рассеяния. (Тема 15) тела и вещества 6 класс 1
тела и вещества 6 класс 1 Нарезание резьбы на деталях
Нарезание резьбы на деталях Простые механизмы
Простые механизмы Диэлектрические свойства полимеров
Диэлектрические свойства полимеров Ременная передача
Ременная передача Повышение КПД ГТУ путём внедрения регенеративного цикла
Повышение КПД ГТУ путём внедрения регенеративного цикла Равновесное состояние
Равновесное состояние Основы молекулярно-кинетической теории
Основы молекулярно-кинетической теории Сила. Динамометр
Сила. Динамометр Lek_PP_Operatorny_metod
Lek_PP_Operatorny_metod Задачи по технической механике. Сложение ускорений
Задачи по технической механике. Сложение ускорений Микромир – мир атомов и элементарных частиц
Микромир – мир атомов и элементарных частиц Виды ионизирующего излучения и основные понятия дозиметрии
Виды ионизирующего излучения и основные понятия дозиметрии Биомехатронные системы. Лекция 1. Двойной маятник
Биомехатронные системы. Лекция 1. Двойной маятник Рідинні термометри
Рідинні термометри Второй закон Ньютона
Второй закон Ньютона Решение задач: Гидродинамика. Ламинарное и турбулентное течения жидкостей и газов
Решение задач: Гидродинамика. Ламинарное и турбулентное течения жидкостей и газов Магнитное поле. Тема № 6
Магнитное поле. Тема № 6