Содержание
- 2. Рассмотрим полубесконечную струну, натянутую вдоль оси x. Силу натяжения, которая действует вдоль этой оси, обозначим Т0.
- 3. Тогда от этого источника будет распространяться вдоль оси x волна, уравнение которой имеет вид
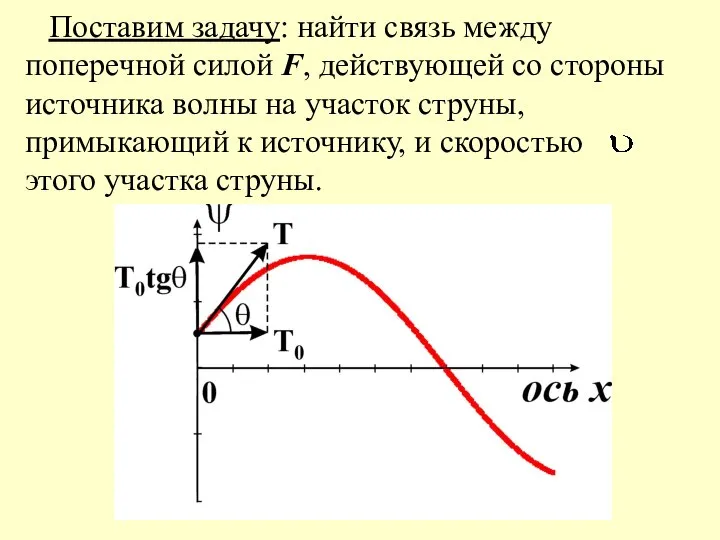
- 4. Поставим задачу: найти связь между поперечной силой F, действующей со стороны источника волны на участок струны,
- 5. Поперечная сила, с которой струна действует на источник волны равна
- 6. Уравнение бегущей волны имеет вид Скорость участка струны равна Следовательно,
- 7. Учитывая, что фазовая скорость волны равна получаем Тогда, связь поперечной силы F и скорости участка струны
- 8. Итак, искомая связь между силой F, действующей со стороны источника волны на участок струны, примыкающий к
- 10. Скачать презентацию






 Правила и приёмы решения задач
Правила и приёмы решения задач Геометрическая оптика. Свет. Источники света
Геометрическая оптика. Свет. Источники света Энергия и работа. Удары. Лекция 3
Энергия и работа. Удары. Лекция 3 Матрица
Матрица Динамика. Законы Ньютона
Динамика. Законы Ньютона Презентация на тему Электрический ток в газах. Плазма
Презентация на тему Электрический ток в газах. Плазма  Лекция 4(ОИ) (студентам)
Лекция 4(ОИ) (студентам) Парабола и ее применение в жизни
Парабола и ее применение в жизни Силы трения между соприкасающимися поверхностями твердых тел
Силы трения между соприкасающимися поверхностями твердых тел Температура. Виды термометров
Температура. Виды термометров Электрическое сопротивление проводников. Единицы сопротивления. Закон Ома для участка цепи
Электрическое сопротивление проводников. Единицы сопротивления. Закон Ома для участка цепи Нефтегазовая и рудная геофизика. Сейсмические методы при изучении строения земной коры
Нефтегазовая и рудная геофизика. Сейсмические методы при изучении строения земной коры Обзор доказательств ложности утверждений о возможности самосовершенствования
Обзор доказательств ложности утверждений о возможности самосовершенствования Автомобильные субкультуры
Автомобильные субкультуры Методы измерения фокусных расстояний
Методы измерения фокусных расстояний Ускорение свободного падения на Земле и других планетах. 9 класс
Ускорение свободного падения на Земле и других планетах. 9 класс Кинематика в профессиональной деятельности
Кинематика в профессиональной деятельности Исследование радиального профиля параметров активной среды лазеров с разрядом в полом катоде
Исследование радиального профиля параметров активной среды лазеров с разрядом в полом катоде Flyer engine BYD 368
Flyer engine BYD 368 Проект Электромагнитный двигатель из батарейки
Проект Электромагнитный двигатель из батарейки Элементарные частицы
Элементарные частицы Электрический ток в металлах
Электрический ток в металлах Электромагнитные волны
Электромагнитные волны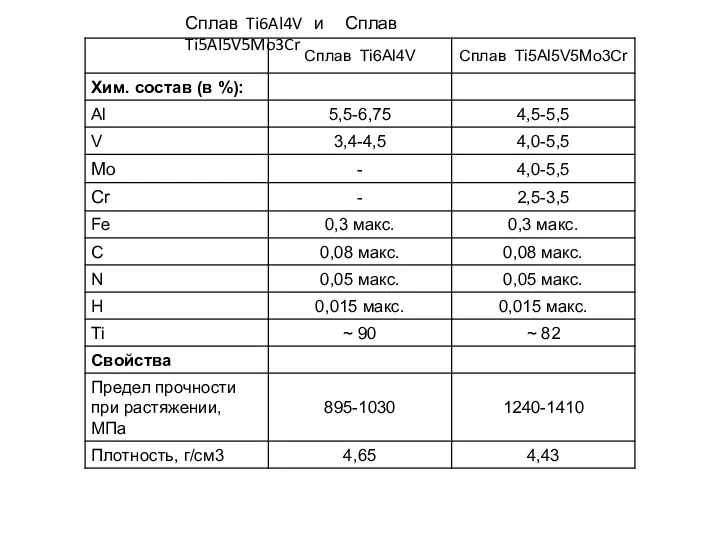 Сплав Ti6Al4V и сплав Ti5Al5V5Mo3Cr
Сплав Ti6Al4V и сплав Ti5Al5V5Mo3Cr Магнитные свойства материалов
Магнитные свойства материалов Презентация на тему Закон Паскаля
Презентация на тему Закон Паскаля  Внутренняя энергия и способы ее изменения
Внутренняя энергия и способы ее изменения Инфракрасное излучение в помощь школе
Инфракрасное излучение в помощь школе