Переменный электрический ток

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
Основные положения теории :
1. Установившиеся вынужденные электромагнитные колебания можно рассматривать как переменный ток, протекающий в цепи, содержащей резистор R, конденсатор C и катушку индуктивности L.
2. Переменный ток можно считать квазистационарным, т.е. мгновенные значения тока можно считать во всех точках цепи одинаковыми, т.к. его изменения являются медленными в сравнении со скоростью распространения ЭМ волны (скоростью света) вдоль этой электрической цепи.
3. Для мгновенных значений квазистационарных токов выполняется закон Ома и следующие из него правила Кирхгофа.
Рассмотрим процессы в простейших электрических цепях с переменным током :
1. Переменный ток течет через резистор R. В рамках условия квазистационарности ток через резистор определяется законом Ома (Е(t) – внешний источник переменной ЭДС):
Амплитуда тока:
Наглядно представить соотношение между переменным током и напряжением в цепи можно векторной диаграммой, построенной для амплитудных значений гармонических функций тока I(t) и напряжения U(t) .
(1)
Из векторной диаграммы видно: сдвиг фаз между амплитудой тока Im , текущего через резистор, и падением напряжения на резисторе URm , равен нулю.
(2)

2. Переменный ток течет через катушку индуктивности L. Под действием переменной ЭДС Е(t) в цепи течет переменный, приводящий к возникновению ЭДС самоиндукции в катушке. Закон Ома :
(3)
Выделим из (3) дифференциал тока dI и проинтегрируем по времени (постоянная интегрирования равна нулю, т.к. отсутствует постоянный ток):
(4)
Из (4) получаем реактивное индуктивное сопротивление катушки (для постоянного тока, ω = 0, получаем ZL = 0 ) :
(5)
Подставим в (3) выражение амплитуды ЭДС
и получим падение напряжения на катушке:
(7)
(6)
Вывод : из сравнения (4) и (7) следует, что падение напряжения на индуктивности опережает по фазе ток, текущий через катушку, на угол ϕ = π/2 , см. векторную диаграмму.

3. Переменный ток течет через конденсатор С . Под действием переменной ЭДС Е(t) конденсатор непрерывно перезаряжается, в результате в цепи течет переменный ток. Напряжение ЭДС полностью приложено к конденсатору. Пренебрегая сопротивлением проводов, закон Ома запишется в виде :
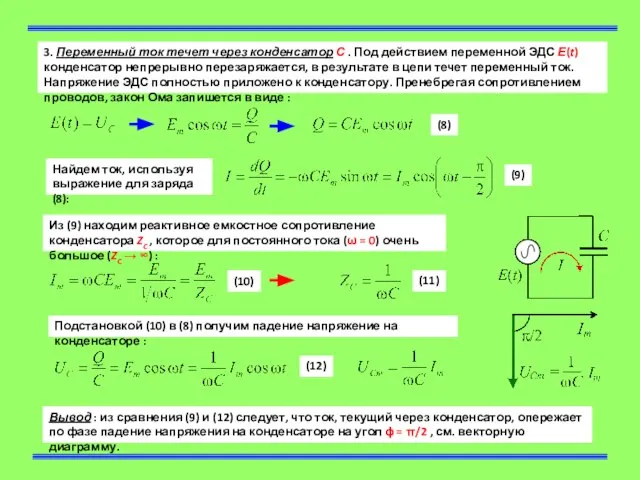
(8)
Найдем ток, используя выражение для заряда (8):
(9)
(10)
Из (9) находим реактивное емкостное сопротивление конденсатора ZC , которое для постоянного тока (ω = 0) очень большое (ZC → ∞) :
Подстановкой (10) в (8) получим падение напряжение на конденсаторе :
(11)
(12)
Вывод : из сравнения (9) и (12) следует, что ток, текущий через конденсатор, опережает по фазе падение напряжения на конденсаторе на угол ϕ = π/2 , см. векторную диаграмму.

СПРАВОЧНЫЙ МАТЕРИАЛ :
Плотность меди: ρ0 = 8,6⋅103 кг/м3
Удельное сопротивление меди: ρ = 0,017 мкОм⋅м
Магнитная постоянная: μ0 = 4π ⋅10−7 Гн/м
Электрическая постоянная: ε0 = 8,85 ⋅10−12 Ф/м
Скорость света в вакууме: с = 3 ⋅108 м/с
5. Закон Ома для переменного тока :
6. Связь между эффективными (действующими) и амплитудными значениями тока и напряжения :
7. Мощность переменного тока :
2. Реактивное сопротивление катушки индуктивности переменному току
(L - индуктивность катушки):
3. Полное сопротивление переменному току последовательной цепи, состоящей из активного сопротивления, электроемкости и индуктивности:
4. Угол сдвига фазы между током и напряжением в последовательной цепи, содержащей активное сопротивление, электроемкость и индуктивность :
1. Реактивное сопротивление конденсатора переменному току (C – электроемкость конденсатора; ω - круговая частота) :
Основные формулы для решения задач

А1. (В.14.23) Найти полное сопротивление цепи Z и разность фаз между напряжением и током при разных способах включения сопротивления R, емкости С и индуктивности L. Рассмотреть следующие случаи : 1). R и С включены последовательно; 2). R и С включены параллельно; 3). R и L включены последовательно; 4). R и L включены параллельно; 5). R, L и С включены последовательно.
1). Цепь переменного тока из последовательно соединенных резистора конденсатора С и R. В цепи под действием переменной ЭДС Е(t) возникает переменный ток, создающий падения напряжения на каждом из элементов цепи. Закон Ома запишется в виде :
(1)
Угол ϕ определяет разность фаз между силой тока и напряжением ЭДС на зажимах цепи :
Амплитуда напряжения ЭДС – это гипотенуза треугольника:
Амплитуда тока :
Полное сопротивление цепи:
Реактивное сопротивление цепи:
Из векторной диаграммы видно, что вектор амплитуды ЭДС Еm равен векторной сумме амплитуд напряжений на элементах цепи.

2). Цепь переменного тока из параллельно соединенных резистора R и конденсатора С. В цепи под действием переменной ЭДС Е(t) возникает переменный ток, создающий падения напряжения на каждом из элементов цепи. Закон Ома запишется в виде :
Угол ϕ определяет разность фаз между током
в цепи и напряжением ЭДС на зажимах цепи :
Амплитуда тока :
Полное сопротивление цепи :
Из векторной диаграммы видно, что вектор амплитуды тока
Im равен векторной сумме амплитуд тока в элементах цепи :

3). Цепь переменного тока из последовательно соединенных резистора R и индуктивности L. В цепи под действием ЭДС Е(t) возникает переменный ток, создающий напряжения на каждом из элементов цепи. Закон Ома имеет вид:
Согласно векторной диаграмме вектор амплитуды ЭДС Еm равен сумме векторов амплитуд напряжений на элементах цепи. Угол ϕ определяет разность фаз между током и напряжением ЭДС на зажимах цепи :
Амплитуда тока из (3) :
Полное сопротивление цепи :
Реактивное сопротивление цепи :

4). Цепь переменного тока из последовательно соединенных резистора R, конденсатора С и катушки индуктивности L . В цепи под действием переменной ЭДС Е(t) возникает переменный ток, создающий падения напряжения на каждом из элементов цепи. Закон Ома запишется в виде :
Из векторной диаграммы видно, что вектор амплитуды ЭДС Еm равен векторной сумме амплитуд падений напряжений на элементах цепи. Угол ϕ определяет разность фаз между силой тока в цепи и напряжением ЭДС на зажимах цепи :
Амплитуда напряжения ЭДС – это гипотенуза прямоугольного треугольника:
Амплитуда тока :
Полное сопротивление цепи :
Реактивное сопротивление цепи :

А2. (В.14.24) Конденсатор емкостью С = 1 мкФ и резистор с сопротивлением R = 3 кОм включены в цепь переменного тока с частотой ν = 50 Гц. Найти полное сопротивление цепи, если конденсатор и резистор включены : 1) последовательно; 2) параллельно.
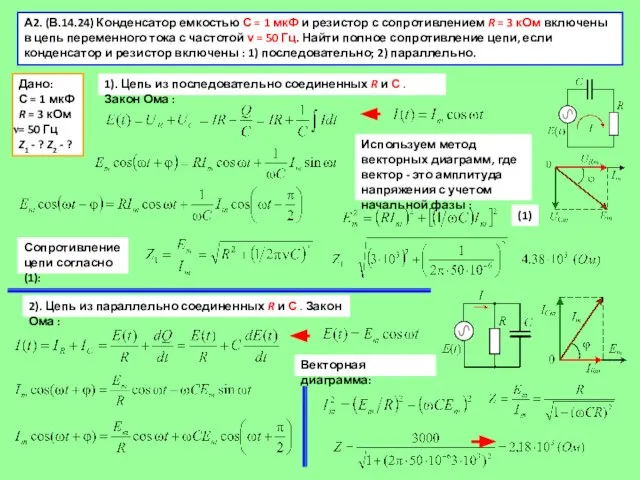
Дано:
С = 1 мкФ
R = 3 кОм
= 50 Гц
Z1 - ? Z2 - ?
1). Цепь из последовательно соединенных R и С . Закон Ома :
Сопротивление цепи согласно (1):
Используем метод векторных диаграмм, где вектор - это амплитуда напряжения с учетом начальной фазы :
2). Цепь из параллельно соединенных R и С . Закон Ома :
Векторная диаграмма:
(1)

Дано :
U = 220 В
= 50 Гц
С = 35,4 мкФ
R = 100 Ом
L = 0,7 Гн
I - ? UС - ?
UR - ? UL - ?
А3. (В.14.25) В цепь переменного тока напряжением U = 220 В и частотой ν = 50 Гц последовательно включены емкости, емкость С = 35,4 мкФ, сопротивление R = 100 Ом и индуктивность L = 0,7 Гн. Найти ток I в цепи и падение напряжения на емкости UС , сопротивлении UR и индуктивности UL .
Закон Ома:
(1)
(2)
Используем метод векторных диаграмм, где вектор - это амплитуда напряжения с учетом начальной фазы :
(3)
Ток в цепи и напряжение на элементах цепи согласно (3):
Сопротивление цепи согласно (3):

А4. (В.14.26) Индуктивность L = 22,6 мГн и сопротивление R включены параллельно в цепь переменного тока с частотой ν = 50 Гц. Найти сопротивление R , если сдвиг фаз между напряжением и током равен ϕ = 60°.
Дано :
L = 22,6 мГн
= 50 Гц
ϕ = 60°
R - ?
Запишем закон Ома и воспользуемся выражением ЭДС самоиндукции :
(2)
Угол ϕ определяет разность фаз между общим током в цепи и напряжением ЭДС на зажимах цепи :
(1)
Амплитуда общего тока цепи согласно векторной диаграмме –
это гипотенуза прямоугольного треугольника с катетами IRm и ILm:

А5. (В.14.27) Активное сопротивление R и индуктивность L соединены параллельно и включены в цепь переменного тока напряжением Е = 127 В и частотой ν = 50 Гц. Найти сопротивление R и индуктивность L, если известно, что цепь поглощает мощность Р = 404 Вт и сдвиг фаз между напряжением и током ϕ = 60°.
(1)
Поглощаемая цепью мощность:
Дано :
Е = 127 В
= 50 Гц
Р = 404 Вт
ϕ = 60°
R - ? L - ?
Из (1) найдем ток:
(2)
Из решения предыдущей задачи для такой же цепи (1) следуют два уравнения, из которых найдем R и L :
Амплитуда общего тока цепи по векторной диаграмме – это гипотенуза треугольника с катетами IRm и ILm:
(3)
(4)
Из (1) и (4) следует :
(5)
После подстановки (5) в (3) получаем :
Из (3) следует :