Содержание
- 2. Идеальный газ - это газ, взаимодействие между молекулами которого пренебрежимо мало. Условия, при выполнении которых газ
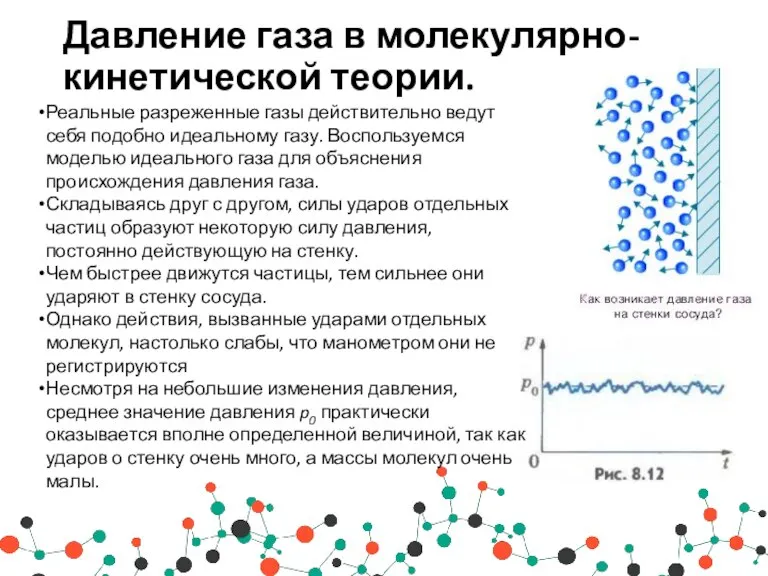
- 3. Давление газа в молекулярно-кинетической теории. Реальные разреженные газы действительно ведут себя подобно идеальному газу. Воспользуемся моделью
- 4. Давление газа в молекулярно-кинетической теории. Вывод: Идеальный газ - модель реального газа. Согласно этой модели молекулы
- 5. Среднее значение квадрата скорости молекул Для вычисления среднего давления надо знать среднюю скорость молекул (точнее, среднее
- 6. Среднее значение квадрата скорости молекул Обозначим модули скоростей отдельных молекул газа через Среднее значение квадрата скорости
- 7. Среднее значение квадрата скорости молекул Видите, из хаоса выплывает определенная закономерность. Учитывая соотношение (8.12), подставим в
- 9. Скачать презентацию





 Закон сохранения импульса
Закон сохранения импульса Механическая работа
Механическая работа Звуковые волны
Звуковые волны СТО РемЗона
СТО РемЗона Роль света в жизни человека
Роль света в жизни человека Применение первого закона термодинамики к различным процессам
Применение первого закона термодинамики к различным процессам Презентация на тему Электронно-лучевая трубка (10 класс)
Презентация на тему Электронно-лучевая трубка (10 класс)  ВКР: Система стеклоочистки лобового стекла
ВКР: Система стеклоочистки лобового стекла Демонтаж устройства самообслуживания
Демонтаж устройства самообслуживания Постоянно изменяемые фазы газораспределения. Системы CVVT
Постоянно изменяемые фазы газораспределения. Системы CVVT Электромагнитные излучения
Электромагнитные излучения Фрикционные передачи
Фрикционные передачи Действие магнитного поля на проводник с током. Сила Ампера. Взаимодействие проводников с током
Действие магнитного поля на проводник с током. Сила Ампера. Взаимодействие проводников с током Электронные фильтры
Электронные фильтры Скорость движения 7 класс
Скорость движения 7 класс Виды теплопередачи: теплопроводность, конвекция, излучение
Виды теплопередачи: теплопроводность, конвекция, излучение Измерение работы и мощности тока в электрической лампе. Лабораторная работа № 7
Измерение работы и мощности тока в электрической лампе. Лабораторная работа № 7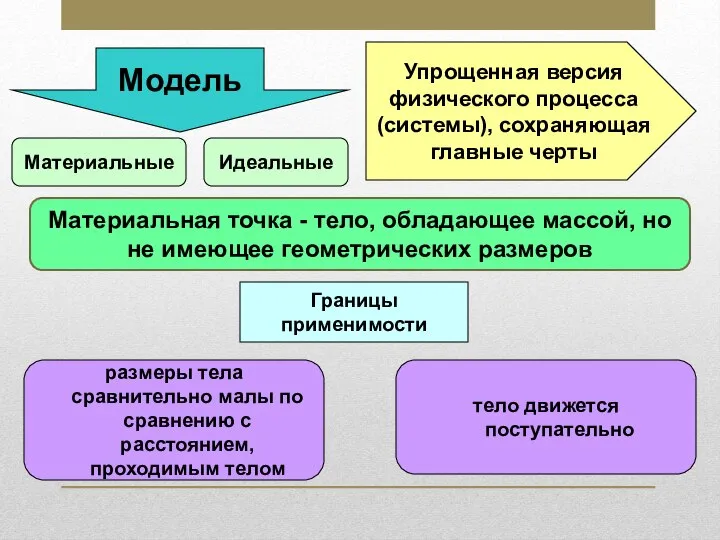 Материальная точка
Материальная точка Потенциальная энергия заряженного тела в однородном электростатическом поле
Потенциальная энергия заряженного тела в однородном электростатическом поле Колебания и волны. Лекция 3.1
Колебания и волны. Лекция 3.1 Ремонт роликового подшипника
Ремонт роликового подшипника Механическая работа. Единицы работы
Механическая работа. Единицы работы Lek_PP_Operatorny_metod
Lek_PP_Operatorny_metod Физические величины, характеризующие организм человека
Физические величины, характеризующие организм человека Действие магнитного поля на проводник с током. Сила ампера. Сила лоренца
Действие магнитного поля на проводник с током. Сила ампера. Сила лоренца Основы конструирования. Базовые навыки работы с наборами
Основы конструирования. Базовые навыки работы с наборами Волновые свойства света
Волновые свойства света Уравнения и диапазоны. Лекция 2
Уравнения и диапазоны. Лекция 2