Содержание
- 2. ЦЕЛЬ: ВЫПОЛНЕНИЕ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ТЕМЕ «ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНЫХ СИЛ И ИЗГИБАЮЩИХ МОМЕНТОВ».
- 3. Рассмотрим тело произвольной формы в “спокойном”, ненагруженном состоянии. Между его частицами всегда существуют силы взаимодействия, которые
- 4. Эпю́ра (фр. epure — чертёж) — особый вид графика, показывающий распределение величины нагрузки на объект. Эпюру
- 5. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ 1. Определение реакций опор балки и выполнение проверки; 2. Определение поперечных сил (Q)
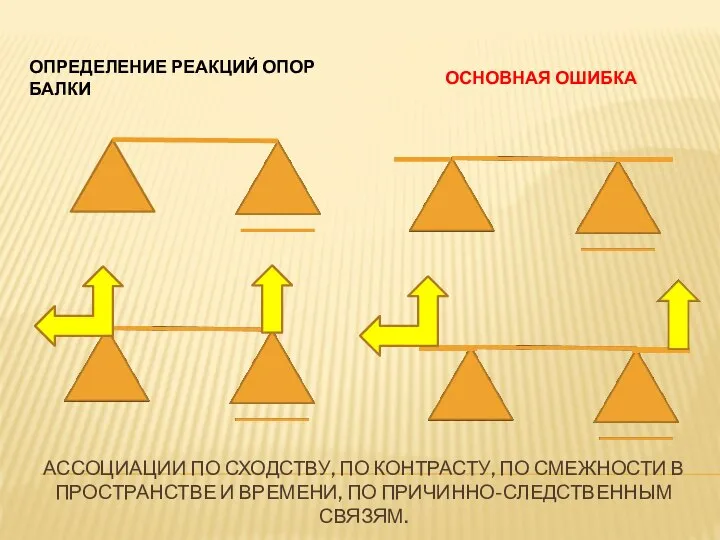
- 6. АССОЦИАЦИИ ПО СХОДСТВУ, ПО КОНТРАСТУ, ПО СМЕЖНОСТИ В ПРОСТРАНСТВЕ И ВРЕМЕНИ, ПО ПРИЧИННО-СЛЕДСТВЕННЫМ СВЯЗЯМ. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ
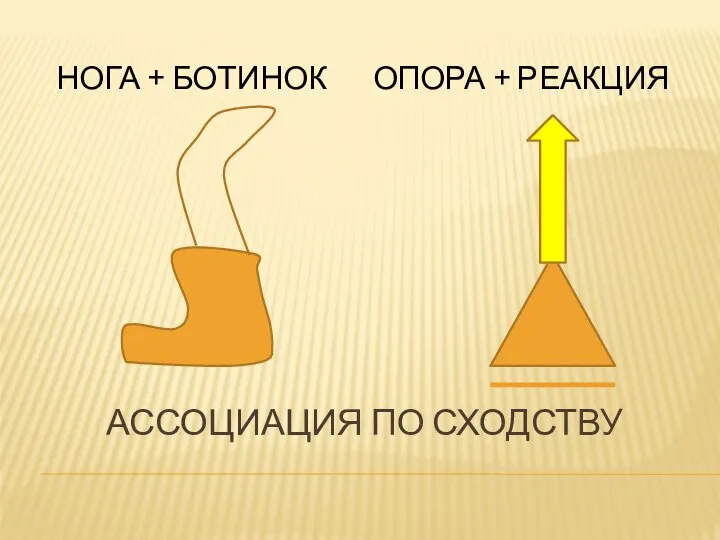
- 7. АССОЦИАЦИЯ ПО СХОДСТВУ НОГА + БОТИНОК ОПОРА + РЕАКЦИЯ
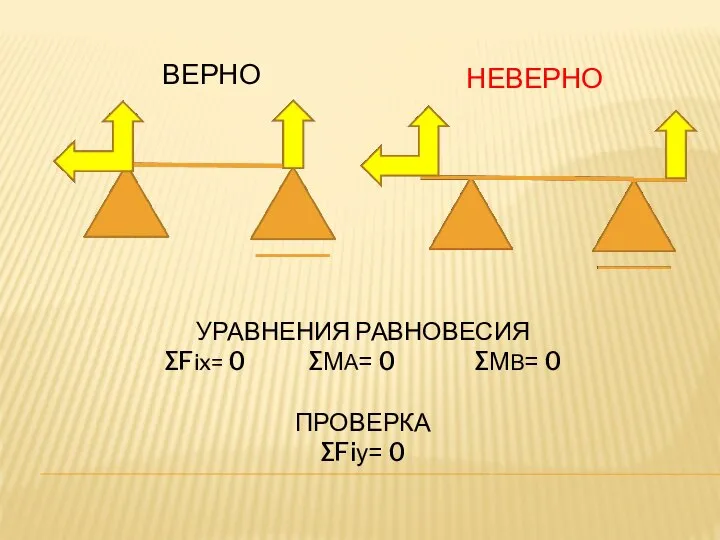
- 8. УРАВНЕНИЯ РАВНОВЕСИЯ ∑Fix= 0 ∑МА= 0 ∑МВ= 0 ПРОВЕРКА ∑Fiу= 0 ВЕРНО НЕВЕРНО
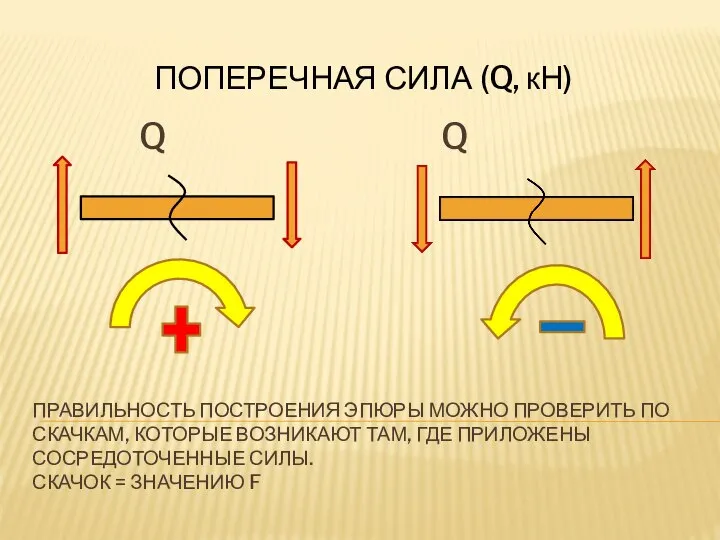
- 9. Q Q ПРАВИЛЬНОСТЬ ПОСТРОЕНИЯ ЭПЮРЫ МОЖНО ПРОВЕРИТЬ ПО СКАЧКАМ, КОТОРЫЕ ВОЗНИКАЮТ ТАМ, ГДЕ ПРИЛОЖЕНЫ СОСРЕДОТОЧЕННЫЕ СИЛЫ.
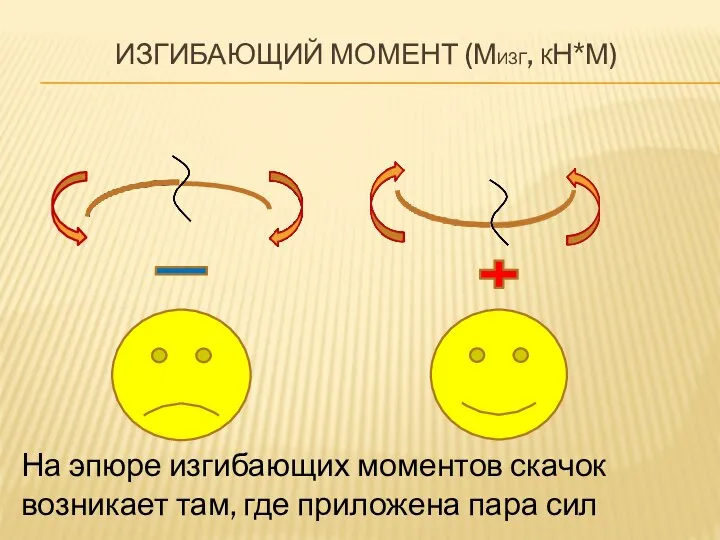
- 10. ИЗГИБАЮЩИЙ МОМЕНТ (МИЗГ, КН*М) На эпюре изгибающих моментов скачок возникает там, где приложена пара сил
- 11. ПРОВЕРКА ПРАВИЛЬНОСТИ ПОСТРОЕНИЯ ЭПЮР
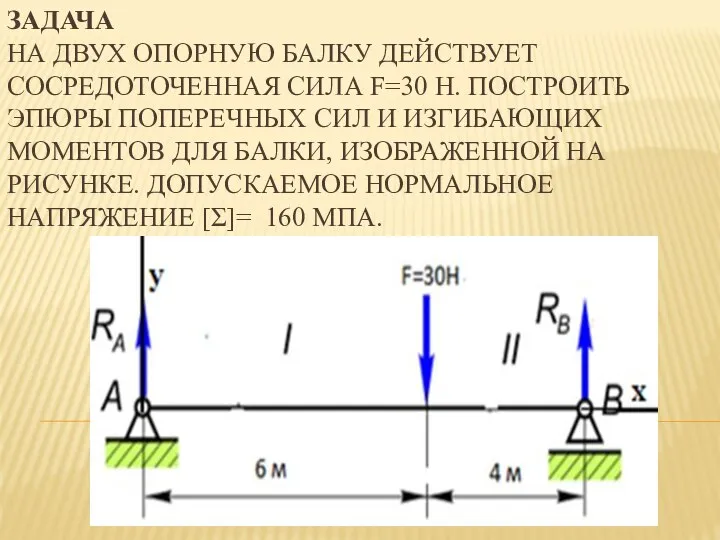
- 12. ЗАДАЧА НА ДВУХ ОПОРНУЮ БАЛКУ ДЕЙСТВУЕТ СОСРЕДОТОЧЕННАЯ СИЛА F=30 Н. ПОСТРОИТЬ ЭПЮРЫ ПОПЕРЕЧНЫХ СИЛ И ИЗГИБАЮЩИХ
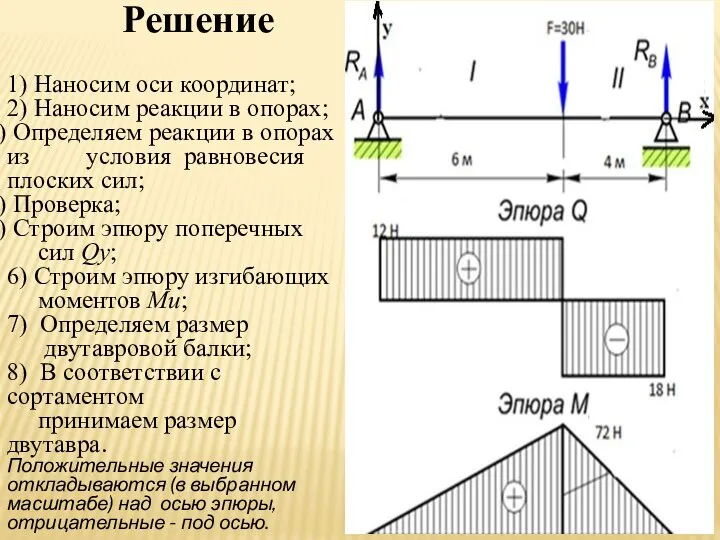
- 13. Решение 1) Наносим оси координат; 2) Наносим реакции в опорах; Определяем реакции в опорах из условия
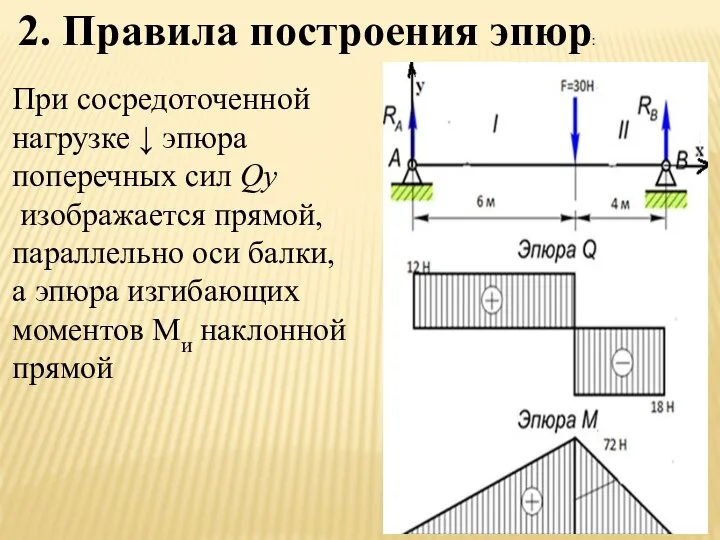
- 14. 2. Правила построения эпюр: При сосредоточенной нагрузке ↓ эпюра поперечных сил Qу изображается прямой, параллельно оси
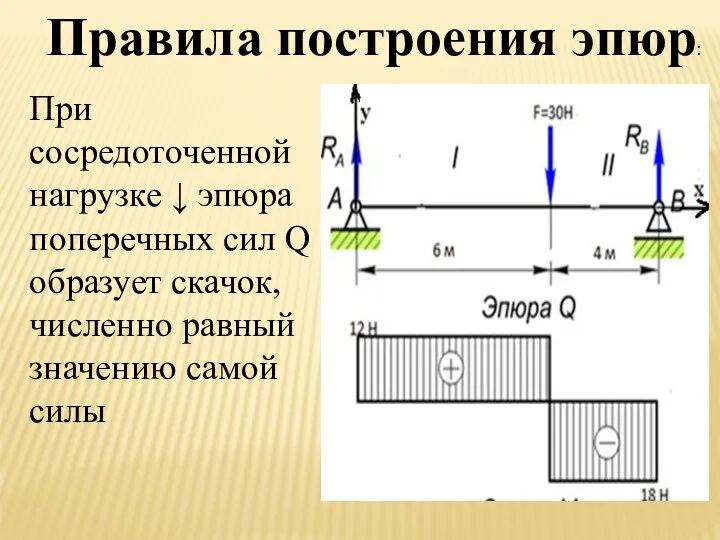
- 15. Правила построения эпюр: При сосредоточенной нагрузке ↓ эпюра поперечных сил Q образует скачок, численно равный значению
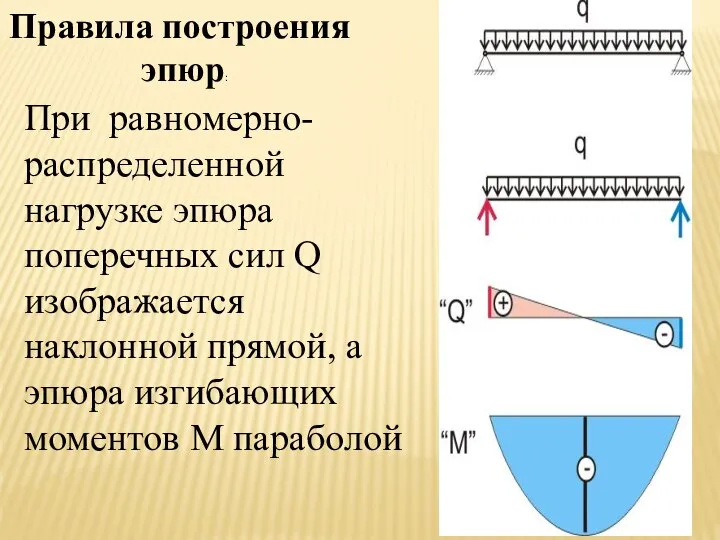
- 16. Правила построения эпюр: При равномерно-распределенной нагрузке эпюра поперечных сил Q изображается наклонной прямой, а эпюра изгибающих
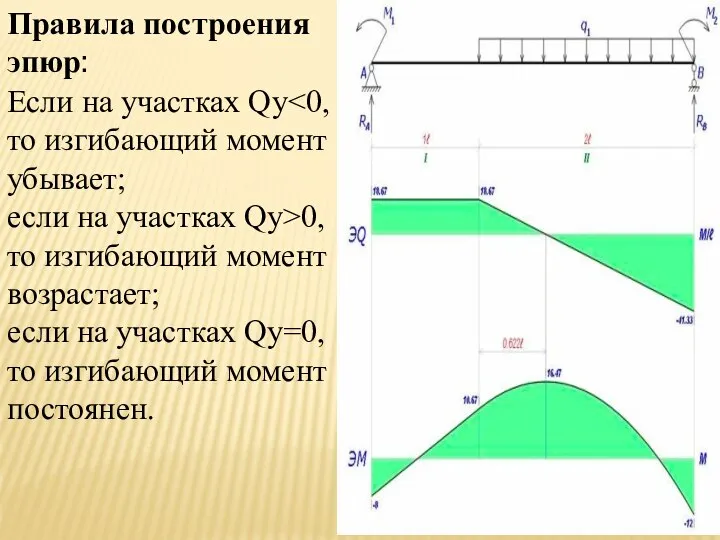
- 17. Правила построения эпюр: Если на участках Qу если на участках Qу>0, то изгибающий момент возрастает; если
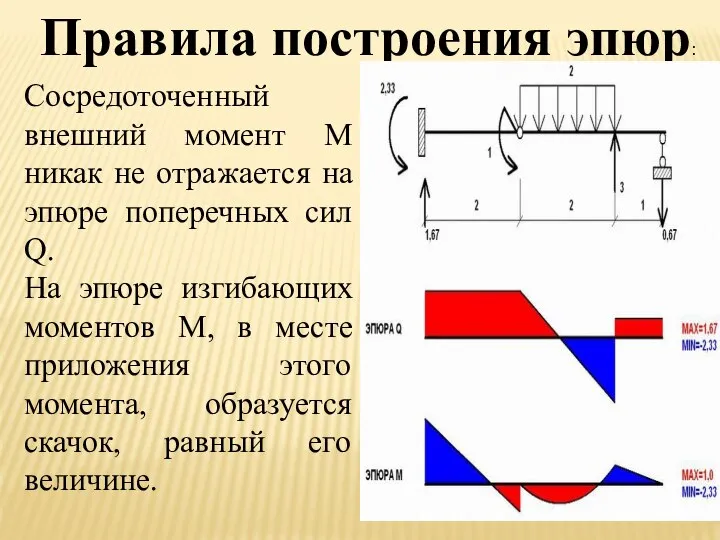
- 18. Правила построения эпюр: Сосредоточенный внешний момент M никак не отражается на эпюре поперечных сил Q. На
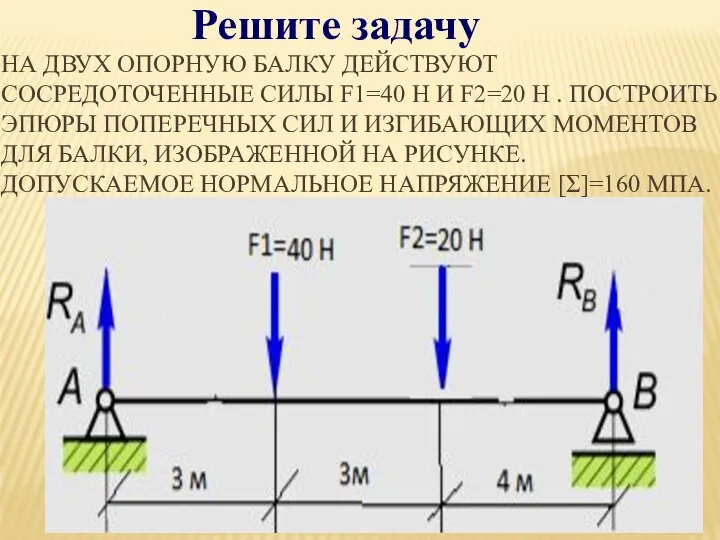
- 19. Решите задачу НА ДВУХ ОПОРНУЮ БАЛКУ ДЕЙСТВУЮТ СОСРЕДОТОЧЕННЫЕ СИЛЫ F1=40 Н И F2=20 Н . ПОСТРОИТЬ
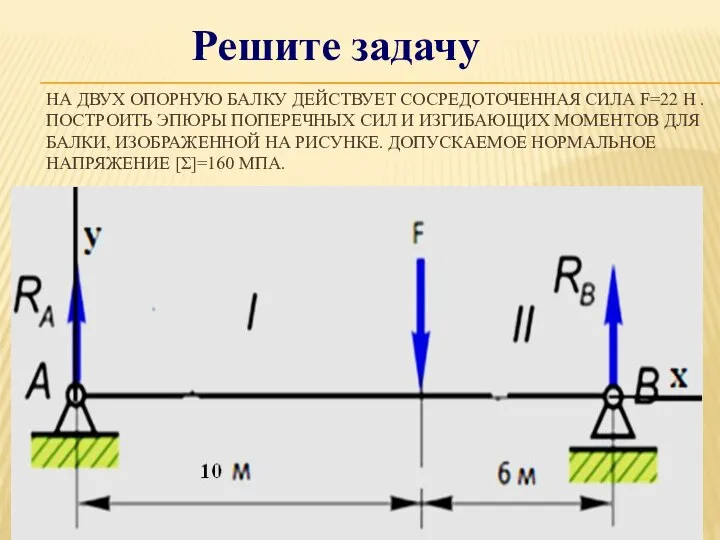
- 20. НА ДВУХ ОПОРНУЮ БАЛКУ ДЕЙСТВУЕТ СОСРЕДОТОЧЕННАЯ СИЛА F=22 Н . ПОСТРОИТЬ ЭПЮРЫ ПОПЕРЕЧНЫХ СИЛ И ИЗГИБАЮЩИХ
- 21. ЗАКЛЮЧЕНИЕ «Ассоциация – это вообще мощная штуковина…. Ты можешь увидеть банан и вспомнить как подбил когда-то
- 23. Скачать презентацию






 Прямолинейного равномерное движение тела
Прямолинейного равномерное движение тела Зарождение теории относительности
Зарождение теории относительности Оборудование для подачи воды из удалённого водоисточника
Оборудование для подачи воды из удалённого водоисточника Презентация на тему Физика вокруг нас
Презентация на тему Физика вокруг нас  Основы антенно-фидерной техники
Основы антенно-фидерной техники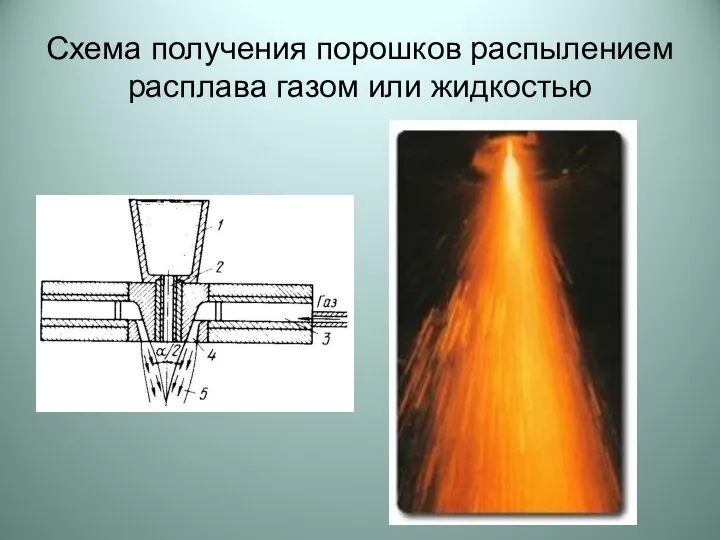 Схема получения порошков распылением расплава газом или жидкостью
Схема получения порошков распылением расплава газом или жидкостью Фильтры с бесконечной импульсной характеристикой. Синтез БИХ-фильтров методом билинейного Z-преобразования''
Фильтры с бесконечной импульсной характеристикой. Синтез БИХ-фильтров методом билинейного Z-преобразования'' Подготовка к ЕГЭ на уроках физики
Подготовка к ЕГЭ на уроках физики Реактивное движение
Реактивное движение Сила тока. Напряжение
Сила тока. Напряжение Потенциальная энергия заряженного тела в однородном электростатическом поле
Потенциальная энергия заряженного тела в однородном электростатическом поле Движение квазичастиц электронов в электрическом поле
Движение квазичастиц электронов в электрическом поле Презентация на тему Источники света. Распространение света
Презентация на тему Источники света. Распространение света  Лента Мёбиуса и Её Свойства
Лента Мёбиуса и Её Свойства Законы Ньютона. Тест
Законы Ньютона. Тест Звуки природы и звуки космоса. Что их объединяет
Звуки природы и звуки космоса. Что их объединяет Рисунки к методичке по теплообменнику
Рисунки к методичке по теплообменнику Механические колебания. Звуковые волны. Акустика
Механические колебания. Звуковые волны. Акустика Юные астрофизики
Юные астрофизики Расчет на прочность при кручении
Расчет на прочность при кручении История создания швейной машины
История создания швейной машины Криволинейное движение тела.Тест
Криволинейное движение тела.Тест Презентация на тему Кинетическая и потенциальная энергия
Презентация на тему Кинетическая и потенциальная энергия 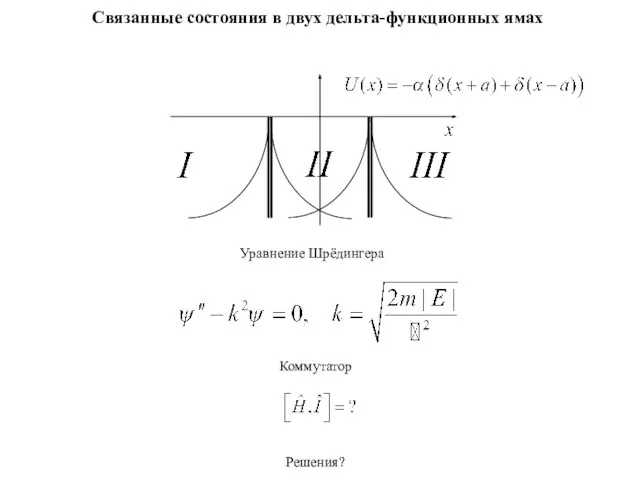 Связанные состояния в двух дельта - функционных ямах
Связанные состояния в двух дельта - функционных ямах Законы сохранения энергии и импульса
Законы сохранения энергии и импульса Физика для химиков. День первый - термодинамика
Физика для химиков. День первый - термодинамика График гармонического колебания
График гармонического колебания История развития физики. Физика и техника
История развития физики. Физика и техника