Потенциальная энергия заряженного тела в однородном электростатическом поле

СОДЕРЖАНИЕ
Работа поля по перемещению заряда ………..........................
Потенциальная энергия заряженного тела .…….…………………
Потенциал электростатического поля…….……………………………
Связь между напряженностью и напряжением ..………………
Поразмыслим……………………………..……………………..………………..

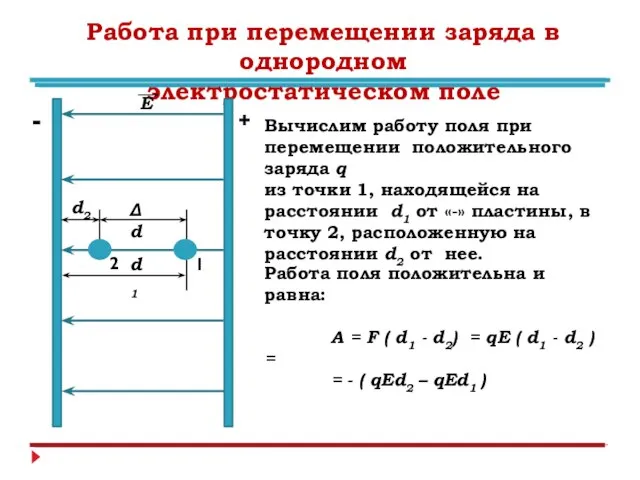
Работа при перемещении заряда в однородном
электростатическом поле
+
-
Е
1
2
d1
d2
Δd
Вычислим работу поля при перемещении положительного заряда q
из точки 1, находящейся на расстоянии d1 от «-» пластины, в точку 2, расположенную на расстоянии d2 от нее.
Работа поля положительна и равна:
A = F ( d1 - d2) = qE ( d1 - d2 ) =
= - ( qEd2 – qEd1 )

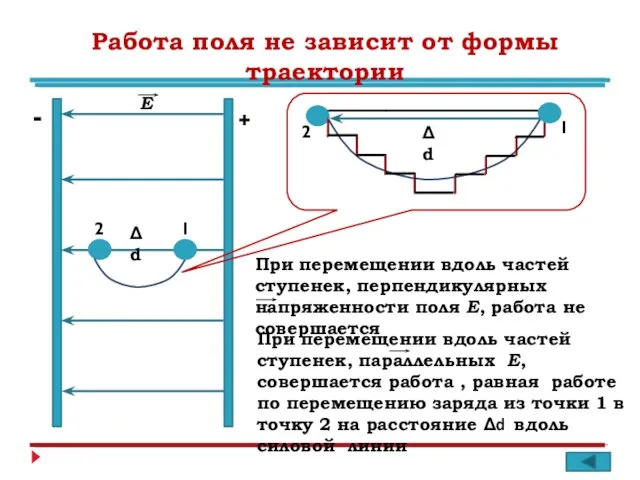
Работа поля не зависит от формы траектории
+
-
1
2
Е
1
2
При перемещении вдоль частей ступенек, перпендикулярных напряженности поля E, работа не совершается
Δd
Δd
При перемещении вдоль частей ступенек, параллельных E, совершается работа , равная работе по перемещению заряда из точки 1 в точку 2 на расстояние Δd вдоль силовой линии

Потенциальная энергия
Известный факт: Если работа не зависит от формы траектории, то она равна изменению потенциальной энергии, взятому с противоположным знаком, т.е.
A = – (Wp2 – Wp1 ) = – ΔWp
Ранее мы получили формулу: A = – (qEd2 – qEd1 )
Очевидно, что потенциальная энергия заряда в однородном
электростатическом поле равна: Wp = qEd
Важные зависимости
Если A > 0, то ΔWp < 0 – потенциальная энергия заряженного тела уменьшается, а кинетическая энергия возрастает;
Если A < 0, то ΔWp > 0 – потенциальная энергия возрастает, а кинетическая энергия уменьшается;
Если А = 0, то ΔWp= 0 – потенциальная энергия не изменяется и кинетическая энергия постоянна.
! ! ! На замкнутой траектории работа поля равна нулю

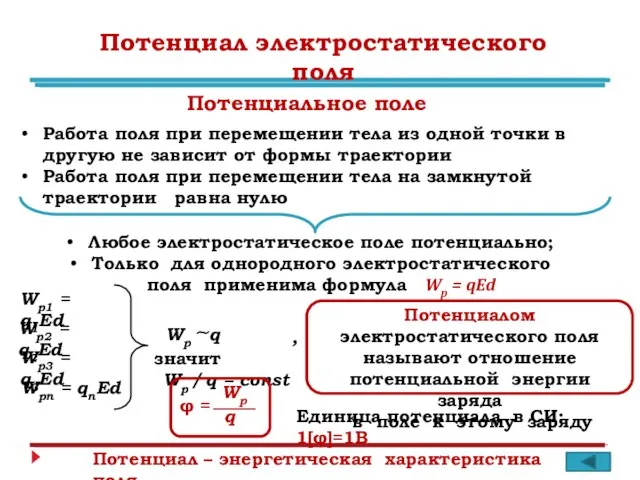
Потенциал электростатического поля
Работа поля при перемещении тела из одной точки в другую не зависит от формы траектории
Работа поля при перемещении тела на замкнутой траектории равна нулю
Потенциальное поле
Любое электростатическое поле потенциально;
Только для однородного электростатического поля применима формула Wp = qEd
Wp1 = q1Ed
Wp2 = q2Ed
Wp3 = q3Ed
Wpn = qnEd
, значит
Wp / q = const
Потенциалом электростатического поля называют отношение потенциальной энергии заряда
в поле к этому заряду
Потенциал – энергетическая характеристика поля
Единица потенциала в СИ: 1[φ]=1B

Разность потенциалов
Значение потенциала в данной точке зависит от выбора нулевого уровня для отсчета потенциала
Изменение же потенциала от выбора нулевого уровня отсчета потенциала не зависит.
Wp = q φ
Α = – (Wp2 – Wp1) = – q ( φ2 – φ1) = q ( φ1 – φ2) = qU
где U = φ1 – φ2 - разность потенциалов, т. е. разность значений
потенциала в начальной и конечной точках траектории
U = φ1 – φ2 = Α /q
Разность потенциалов ( напряжение) между двумя точками равна отношению работы поля при перемещении заряда из начальной точки в конечную к этому заряду.
Единица разности потенциалов в СИ: 1[U] = 1Дж/ Кл = 1 В

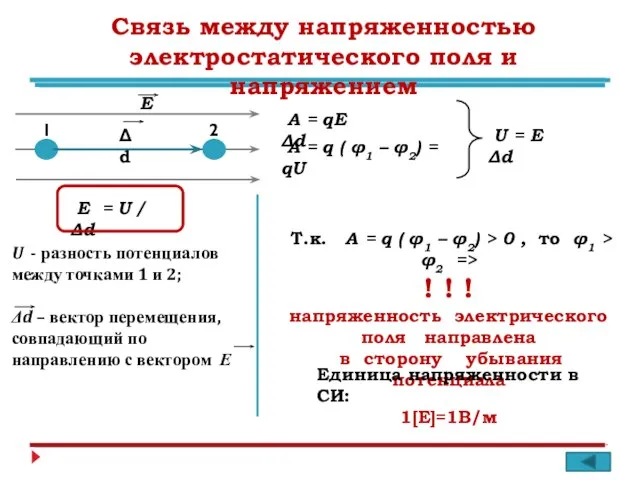
Связь между напряженностью электростатического поля и напряжением
1
2
Δd
Е
A = qE Δd Α = q ( φ1 – φ2) = qU
U = E Δd
Е = U / Δd
U - разность потенциалов
между точками 1 и 2;
Δd – вектор перемещения, совпадающий по направлению с вектором Е
Т.к. Α = q ( φ1 – φ2) > 0 , то φ1 > φ2 =>
! ! !
напряженность электрического поля направлена
в сторону убывания потенциала
Единица напряженности в СИ:
1[E]=1B/м

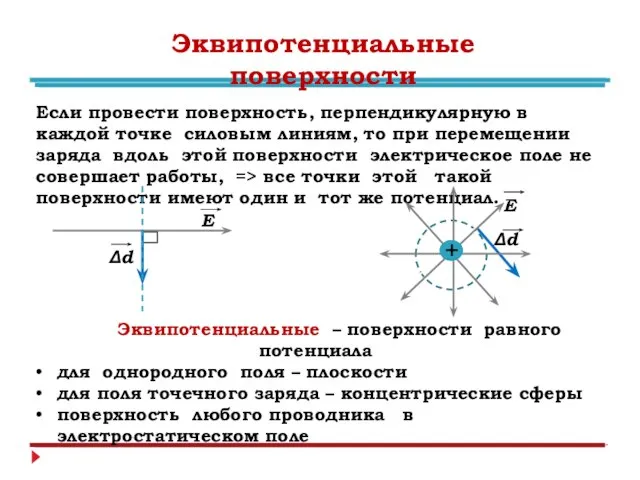
Эквипотенциальные поверхности
Если провести поверхность, перпендикулярную в каждой точке силовым линиям, то при перемещении заряда вдоль этой поверхности электрическое поле не совершает работы, => все точки этой такой поверхности имеют один и тот же потенциал.
Эквипотенциальные – поверхности равного потенциала
для однородного поля – плоскости
для поля точечного заряда – концентрические сферы
поверхность любого проводника в электростатическом поле
Е
Δd
Е
Δd

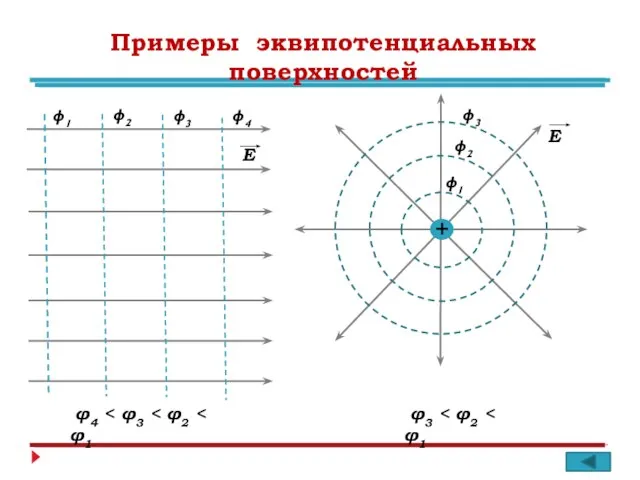
Примеры эквипотенциальных поверхностей
φ1
φ2
φ3
φ4
φ4 < φ3 < φ2 < φ1
Е
Е
φ1
φ2
φ3
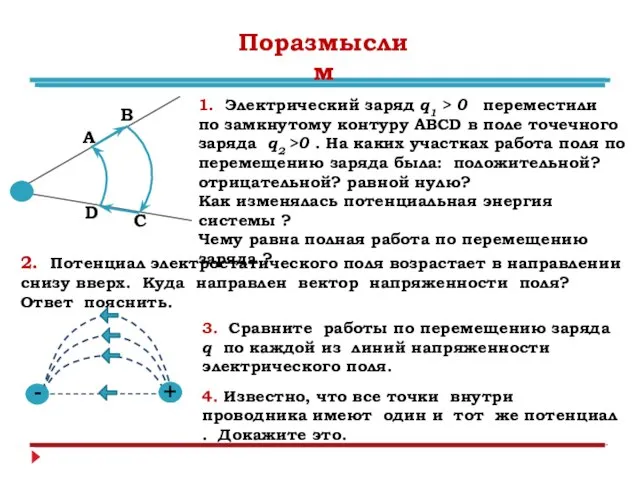
φ3 < φ2 < φ1

А
В
С
D
Поразмыслим
1. Электрический заряд q1 > 0 переместили
по замкнутому контуру АВСD в поле точечного заряда q2 >0 . На каких участках работа поля по перемещению заряда была: положительной? отрицательной? равной нулю?
Как изменялась потенциальная энергия системы ?
Чему равна полная работа по перемещению заряда ?
2. Потенциал электростатического поля возрастает в направлении снизу вверх. Куда направлен вектор напряженности поля? Ответ пояснить.
3. Сравните работы по перемещению заряда q по каждой из линий напряженности электрического поля.
+
-
4. Известно, что все точки внутри проводника имеют один и тот же потенциал . Докажите это.

Решите и запишите
Какую работу совершает электрическое поле при перемещении заряда
2 нКл из точки с потенциалом 20 В в точку с потенциалом 200 В?
Дано:
q = 2нКл = 2 х 10 -9 Кл
φ1= 20 B
φ2= 200 B
___________________________
А - ?
Решение:
Α = q ( φ1 – φ2) = 2 х10 -9 Кл (20 В – 200 В ) =
= – 0,36 мкДж.
Ответ: А = 0,36 мкДж.
2. Поле образовано зарядом 17 нКл. Какую работу надо совершить, чтобы одноименный заряд 4 нКл перенести из точки, удаленной от первого заряда на 0,5 м в точку, удаленную от него на 0,05 м?
Дано:
q1 = 17нКл = 17 х 10 -9 Кл
d1= 0,5 м; d2= 0,05 м;
q2= 4 нКл = 4 х10 -9 Кл
А - ?
Решение:
A =q2Ed2 – q2Ed1 = kq2 q1 ( 1/d2 – 1/d1) =
= 11 мкДж
Ответ: А = 11 мкДж.