способы решения
Система уравнений Максвелла для электромагнитного поля: смысл, способы решения
Полезно знать Подготовка к экзамену Физика для "чайников"
Иван27 Июнь 201717 264
Нет времени писать работу?
Доверь это кандидату наук!
Узнай стоимость
Содержание
Содержание
Первое уравнение Максвелла
Третье уравнение Максвелла
Второе уравнение Максвелла
Четвертое уравнение Максвелла
Уравнения Максвелла в электродинамике – это как законы Ньютона в классической механике или как постулаты Эйнштейна в теории относительности. Фундаментальные уравнения, в сущности которых мы сегодня будем разбираться, чтобы не впадать в ступор от одного их упоминания.
Уравнения Максвелла – это система уравнений в дифференциальной или интегральной форме, описывающая любые электромагнитные поля, связь между токами и электрическими зарядами в любых средах.
Уравнения Максвелла неохотно принимались и критически воспринимались учеными-современниками Максвелла. Все потому, что эти уравнения не были похожи ни на что из известного людям ранее.
Тем не менее, и по сей день нет никаких сомнений в правильности уравнений Максвелла, они «работают» не только в привычном нам макромире, но и в области квантовой механики.
Уравнения Максвелла совершили настоящий переворот в восприятии людьми научной картины мира. Так, они предвосхитили открытие радиоволн и показали, что свет имеет электромагнитную природу.
Джеймс Клерк Максвелл
(1831–1879),




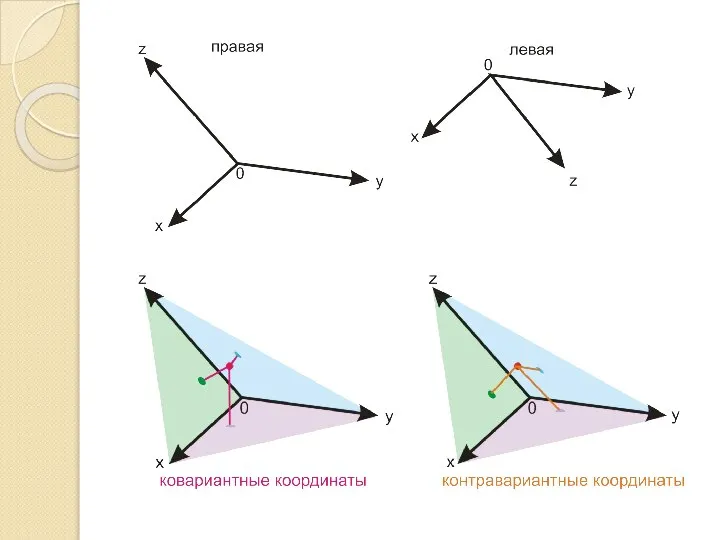
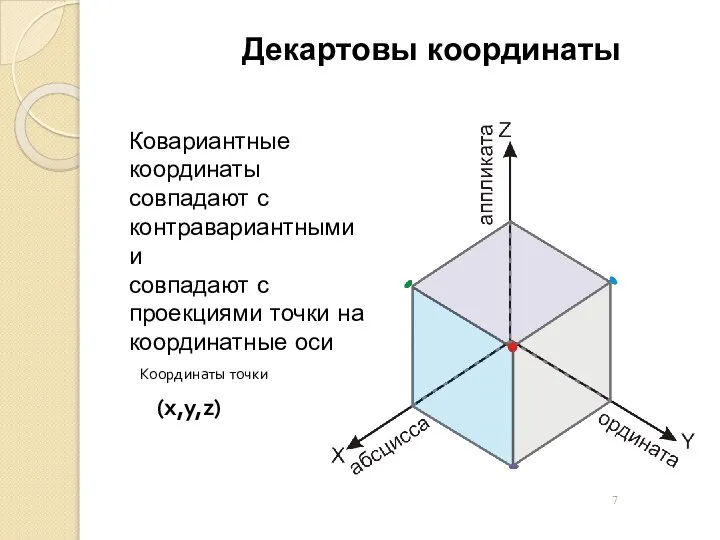
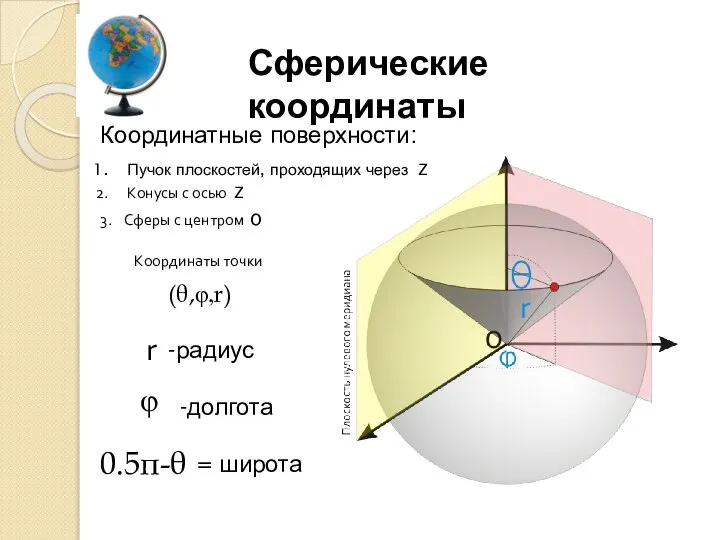
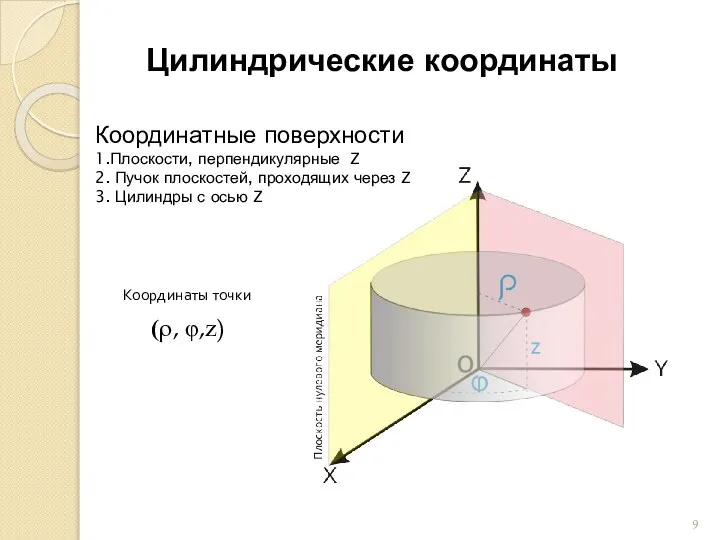








 Задача на преломление луча в плоскопараллельной пластине
Задача на преломление луча в плоскопараллельной пластине Механическое движение
Механическое движение Получение переменной ЭДС. Сопротивление, индуктивность и емкость в цепи переменного тока
Получение переменной ЭДС. Сопротивление, индуктивность и емкость в цепи переменного тока Матрицы плотности
Матрицы плотности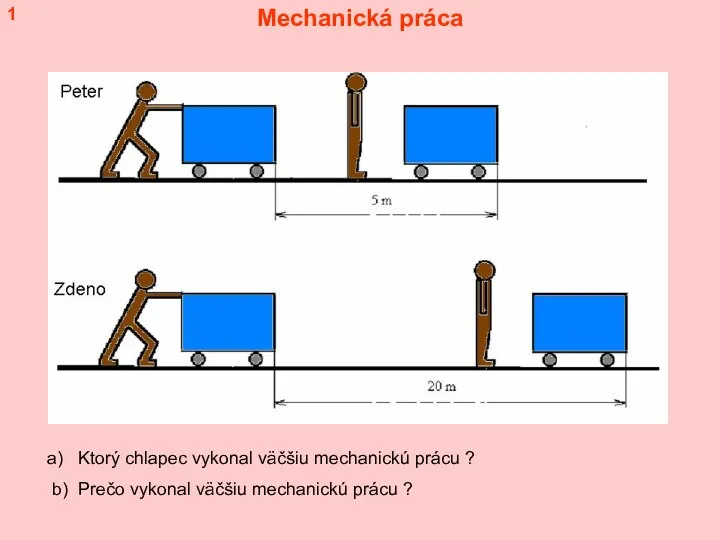 Mechanická práca
Mechanická práca Подвеска
Подвеска Определение рациональных параметров оборудования теплового действия к ковшовым рабочим органам для земляных работ
Определение рациональных параметров оборудования теплового действия к ковшовым рабочим органам для земляных работ Сообщающиеся сосуды
Сообщающиеся сосуды Давление. Обобщение
Давление. Обобщение Ответы на вопросы
Ответы на вопросы Лабораторная работа Определение положения центра тяжести плоской фигуры
Лабораторная работа Определение положения центра тяжести плоской фигуры Електричні двигуни
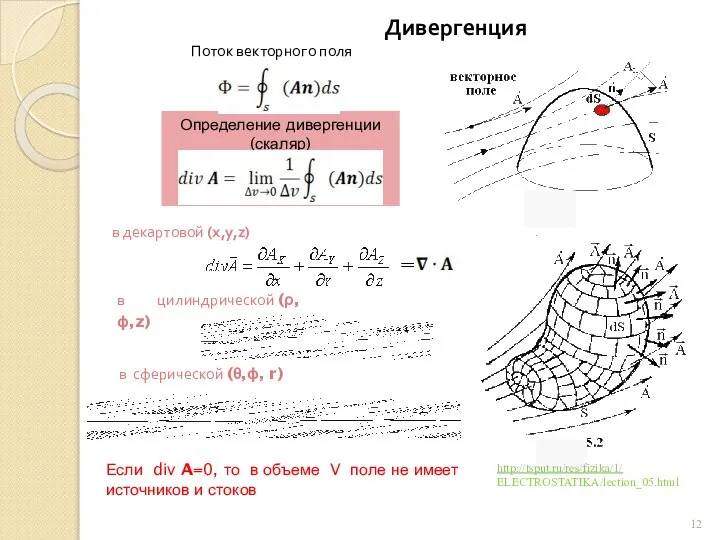
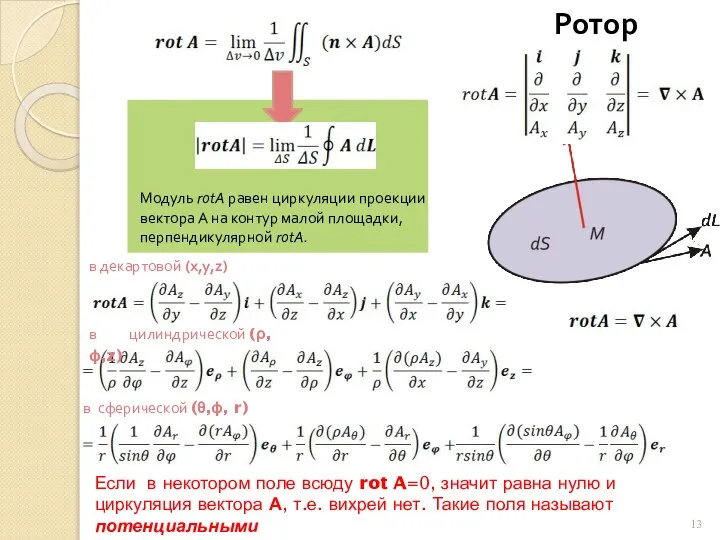
Електричні двигуни Вихрь (ротор) векторного поля
Вихрь (ротор) векторного поля Кинематика
Кинематика Плотность. Способы измерения плотности
Плотность. Способы измерения плотности Кульова блискавка
Кульова блискавка Історія вивчення магнетизму
Історія вивчення магнетизму Энергетические методы расчёта упругих систем
Энергетические методы расчёта упругих систем Магнитные бури
Магнитные бури Теоретические основы разработки полимерных композиционных материалов триботехнического назначения. Задание на КП
Теоретические основы разработки полимерных композиционных материалов триботехнического назначения. Задание на КП Работа и мощность
Работа и мощность Innovative methods to improve the efficiency of power units of thermal and nuclear power plants
Innovative methods to improve the efficiency of power units of thermal and nuclear power plants Смена естественнонаучных картин мира
Смена естественнонаучных картин мира Проектирование и укрепление откосов от размыва
Проектирование и укрепление откосов от размыва Формирование гибких технологий и ремонта системы питания газобаллонных автомобилей
Формирование гибких технологий и ремонта системы питания газобаллонных автомобилей задачи на равноускоренное движение (1)
задачи на равноускоренное движение (1) Йондоҙ булып ҡойола, мамыҡ булып йыйыла
Йондоҙ булып ҡойола, мамыҡ булып йыйыла Презентация на тему Развитие средств связи
Презентация на тему Развитие средств связи